安徽省滁州市2023年中考一模数学试卷
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
1. 下列各数中,最大的数是( )A、1 B、0 C、-2 D、2. 截至2022年10月,我国基本医疗保险参保人数已超过13.6亿人,其中数据13.6亿用科学记数法表示为( )A、 B、 C、 D、3. 如图是四个完全相同的小正方体搭成的几何体,它的俯视图为( )
 A、
A、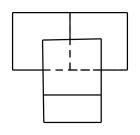 B、
B、 C、
C、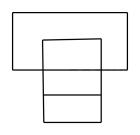 D、
D、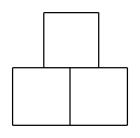 4. 下列计算正确的是( )A、 B、 C、 D、5. 有A,B,C三个小球,按如图所示的方式悬挂在天花板上,每次摘下一个小球且摘A之前需先摘下B,直到3个小球都被摘下,则第二个摘下的小球是A的概率是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 有A,B,C三个小球,按如图所示的方式悬挂在天花板上,每次摘下一个小球且摘A之前需先摘下B,直到3个小球都被摘下,则第二个摘下的小球是A的概率是( )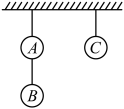 A、 B、 C、 D、6. 将一把直尺和一块含有角的直角三角板按如图所示方式放置,直角三角板的一个顶点在直尺一边上,若 , 则的度数为( )
A、 B、 C、 D、6. 将一把直尺和一块含有角的直角三角板按如图所示方式放置,直角三角板的一个顶点在直尺一边上,若 , 则的度数为( ) A、 B、 C、 D、7. 如图,P是反比例函数的图象上一点,过点P分别作x轴,y轴的平行线,交反比例函数的图象于点M,N,则的面积为( )
A、 B、 C、 D、7. 如图,P是反比例函数的图象上一点,过点P分别作x轴,y轴的平行线,交反比例函数的图象于点M,N,则的面积为( ) A、1 B、1.2 C、2 D、2.48. 某厂家2022年月份的自行车产量统计图如图所示,3月份自行车产量不小心被墨汁覆盖.若2月份到4月份该厂家自行车产量的月增长率都相同,则3月份自行车产量为( )
A、1 B、1.2 C、2 D、2.48. 某厂家2022年月份的自行车产量统计图如图所示,3月份自行车产量不小心被墨汁覆盖.若2月份到4月份该厂家自行车产量的月增长率都相同,则3月份自行车产量为( ) A、218辆 B、240辆 C、256辆 D、272辆9. 已知点在直线上,且 , 则下列不等关系一定成立的是( )A、 B、 C、 D、10. 如图,在正方形中, , G是的中点,点E是正方形内一动点,且 , 连接 , 将线段绕点D逆时针旋转90°得到线段 , 连接 , 则线段长的最小值是( )
A、218辆 B、240辆 C、256辆 D、272辆9. 已知点在直线上,且 , 则下列不等关系一定成立的是( )A、 B、 C、 D、10. 如图,在正方形中, , G是的中点,点E是正方形内一动点,且 , 连接 , 将线段绕点D逆时针旋转90°得到线段 , 连接 , 则线段长的最小值是( ) A、 B、2 C、3 D、
A、 B、2 C、3 D、二、填空题
-
11. 因式分解: .12. 如图,四边形为菱形,点E是的中点,点F,H是对角线上两点,且 , 点G在边上.若四边形是矩形,则菱形的周长为 .
 13. 如图,为的直径, , , 劣弧的长是劣弧长的2倍,则的长为 .
13. 如图,为的直径, , , 劣弧的长是劣弧长的2倍,则的长为 . 14. 已知抛物线(m是常数,且)经过点 .(1)、该抛物线的顶点坐标为;(2)、若一次函数的图象与二次函数的图象的交点坐标分别是 , 且 , 则的最大值为 .
14. 已知抛物线(m是常数,且)经过点 .(1)、该抛物线的顶点坐标为;(2)、若一次函数的图象与二次函数的图象的交点坐标分别是 , 且 , 则的最大值为 .三、解答题
-
15. 计算: .16. 如图,在每个小正方形的边长为1个单位的网格中,的顶点均在格点(网格线的交点)上.

⑴将线段先向左平移2个单位,再向下平移2个单位,得到线段 , 画出线段 , 再将线段绕点顺时针旋转得到 , 画出线段;
⑵在给定的网格中,以点为位似中心,将线段放大为原来的2倍,得到线段 , 画出线段 .
17. 为美化市容,某广场要在人行雨道上用10×20的灰、白两色的广场砖铺设图案,设计人员画出的一些备选图案如图所示.
[观察思考]图1灰砖有1块,白砖有8块;图2灰砖有4块,白砖有12块;以此类推.
(1)、[规律总结]图4灰砖有块,白砖有块;图n灰砖有块时,白砖有块;(2)、[问题解决]是否存在白砖数恰好比灰砖数少1的情形,请通过计算说明你的理由.18. 已知 .(1)、化简A;(2)、当 , 时,求A的值.19. 某风景区,风轩亭B在翠微阁A的正南方向,两个景点被一座小山阻隔,计划在A、B之间修建一条直通景观隧道(如图).为测量A、B两点之间距离,在一条东西方向的公路l上选择P、Q两点分别观测A、B,已知点A在点P的北偏东方向上,点B在点Q的北偏东方向上,米,米,试求A、B两点之间的距离.(精确到1米,其中 , ) 20. 如图,是⊙O的直径,是⊙O上异于的两点,且 , 过点C作交的延长线于点F,交的延长线于点E,连接 .
20. 如图,是⊙O的直径,是⊙O上异于的两点,且 , 过点C作交的延长线于点F,交的延长线于点E,连接 . (1)、求证:是⊙O的切线;(2)、若 , , 求的长.21. 2022年是名副其实的金砖“中国年”,在各方的积极支持下,我国成功举办了70多场会议和活动,涵盖政治安全、经贸财经、人文交流、可持续发展和公共卫生等领域,推动金砖合作在多方面取得重要进展.某校进行了以2022金砖“中国年”为主题的时事竞赛活动,第一批选取15位同学的成绩,后又追加了5位同学的成绩,并先后对两组数据(即成绩,百分制且为整数)进行收集、整理、描述与分析.下面给出了部分信息:
(1)、求证:是⊙O的切线;(2)、若 , , 求的长.21. 2022年是名副其实的金砖“中国年”,在各方的积极支持下,我国成功举办了70多场会议和活动,涵盖政治安全、经贸财经、人文交流、可持续发展和公共卫生等领域,推动金砖合作在多方面取得重要进展.某校进行了以2022金砖“中国年”为主题的时事竞赛活动,第一批选取15位同学的成绩,后又追加了5位同学的成绩,并先后对两组数据(即成绩,百分制且为整数)进行收集、整理、描述与分析.下面给出了部分信息:a.追加前的15位同学成绩的频数分布直方图如图1(数据分为4组: , , , ).
b.追加前的15位同学在这一组的数据是:82 84 85 87 89 89
c.追加前的15位同学、追加后的20位同学成绩的众数、中位数如表1.

表1
众数
中位数
追加前的位同学
89
追加后的位同学
96
85.5
根据以上信息,回答下列问题:
(1)、写出表1中m的值;(2)、在后追加的5位同学中,成绩大于中位数分的有人;(3)、下列推断合理的是 . (填序号)①若该学校共有750名学生,按追加前的样本估计,参加竞赛活动成绩在80分以上的人数约为500人;
②在追加前的15位同学中,有一位同学的成绩是96分.
22. 抛物线与坐标轴的正半轴分别交于A,B两点,其中 . (1)、如图1,求抛物线的表达式,并求点B的横坐标;(2)、如图2,将抛物线向左平移,使得平移后的抛物线经过点A,且点B的对应点为C,求的长;(3)、如图3,矩形的顶点D,G都在x轴上, , 且 , 把两条抛物线 , 及线段围成的封闭图形的内部记为区域M,要使矩形在区域M的内部(包括边界),求d的取值范围.23. 已知:如图1,△ABC中,AB=AC,BC=6,BE为中线,点D为BC边上一点;BD=2CD,DF⊥BE于点F,EH⊥BC于点H.
(1)、如图1,求抛物线的表达式,并求点B的横坐标;(2)、如图2,将抛物线向左平移,使得平移后的抛物线经过点A,且点B的对应点为C,求的长;(3)、如图3,矩形的顶点D,G都在x轴上, , 且 , 把两条抛物线 , 及线段围成的封闭图形的内部记为区域M,要使矩形在区域M的内部(包括边界),求d的取值范围.23. 已知:如图1,△ABC中,AB=AC,BC=6,BE为中线,点D为BC边上一点;BD=2CD,DF⊥BE于点F,EH⊥BC于点H. (1)、CH的长为;(2)、求BF·BE的值:(3)、如图2,连接FC,求证:∠EFC=∠ABC.
(1)、CH的长为;(2)、求BF·BE的值:(3)、如图2,连接FC,求证:∠EFC=∠ABC.