安徽省亳州市2023年中考二模数学试题
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 2月5日,合肥市统计局发布2022年全市经济运行情况.根据地区生产总值统一核算结果,2022年合肥全市生产总值()为12013.1亿元,连续七年每年跨越一个千亿台阶.数据12013.1亿用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的几何体,它的俯视图是( )
 A、
A、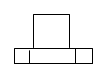 B、
B、 C、
C、 D、
D、 4. 下列各式中,计算结果是的是( )A、 B、 C、 D、5. 如图,已知 , 晓玉把三角板的直角顶点放在直线b上.若 , 则的度数为( )
4. 下列各式中,计算结果是的是( )A、 B、 C、 D、5. 如图,已知 , 晓玉把三角板的直角顶点放在直线b上.若 , 则的度数为( ) A、 B、 C、 D、6. 关于x的一元二次方程有两个不相等的实数根,则k的值不可能是( )A、-2 B、-1 C、0 D、17. 已知 , , , 那么x,y,z满足的等量关系是( )A、 B、 C、 D、8. 如图,在中,直径于点H.若 , , 则的长为( )
A、 B、 C、 D、6. 关于x的一元二次方程有两个不相等的实数根,则k的值不可能是( )A、-2 B、-1 C、0 D、17. 已知 , , , 那么x,y,z满足的等量关系是( )A、 B、 C、 D、8. 如图,在中,直径于点H.若 , , 则的长为( )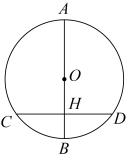 A、5 B、4 C、3 D、29. 九(2)班进行演讲比赛,题目有“我的祖国”“我的梦想”“美丽的家乡”“我的同桌”(分别用字母A,B,C,D依次表示这四个题目).比赛时,将A,B,C,D这四个字母分别写在4张无差别不透明的卡片的正面上,洗匀后正面向下放在桌面上,小进先从中随机抽取一张卡片,放回后洗匀,再由晓晨从中随机抽取一张卡片,则小进和晓晨抽中不同题目的概率为( ).A、 B、 C、 D、10. 如图,抛物线的对称轴是直线 , 图象与x轴交于A,B两点.若 , 则下列结论中错误的是( )
A、5 B、4 C、3 D、29. 九(2)班进行演讲比赛,题目有“我的祖国”“我的梦想”“美丽的家乡”“我的同桌”(分别用字母A,B,C,D依次表示这四个题目).比赛时,将A,B,C,D这四个字母分别写在4张无差别不透明的卡片的正面上,洗匀后正面向下放在桌面上,小进先从中随机抽取一张卡片,放回后洗匀,再由晓晨从中随机抽取一张卡片,则小进和晓晨抽中不同题目的概率为( ).A、 B、 C、 D、10. 如图,抛物线的对称轴是直线 , 图象与x轴交于A,B两点.若 , 则下列结论中错误的是( ) A、 B、 C、 D、若为任意实数,则
A、 B、 C、 D、若为任意实数,则二、填空题
-
11. 因式分解: .12. 若一个直角三角形两条直角边的长分别是一元二次方程的两个实数根,则这个直角三角形斜边的长是 .13. 如图,点A是反比例函数的图象上一点,过点A作轴,交反比例函数的图象于点B.若的面积为2,则m的值为 .
 14. 如图,在中, , 点D是斜边上的一个动点,过点D分别作于点M,于点N.
14. 如图,在中, , 点D是斜边上的一个动点,过点D分别作于点M,于点N. (1)、的度数是;(2)、若 , , 连接 , 当线段有最小值时,线段的长为 .
(1)、的度数是;(2)、若 , , 连接 , 当线段有最小值时,线段的长为 .三、解答题
-
15. 计算: .16. 解分式方程: .17. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
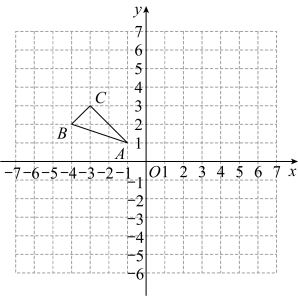
⑴将先向下平移2个单位长度,再向右平移5个单位长度得到 , 画出;
⑵将绕点A按顺时针方向旋转得到 , 画出 .
18. 如图,下列图案都是由同样大小的基本图形按一定规律所组成的,其中:第1个图案中基本图形的个数: ,
第2个图案中基本图形的个数: ,
第3个图案中基本图形的个数: ,
第4个图案中基本图形的个数: ,
…
按此规律排列,解决下列问题:
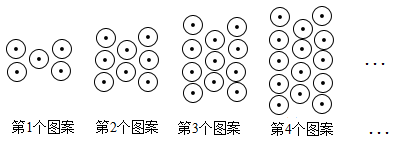 (1)、写出第5个图案中基本图形的个数:=;(2)、如果第n个图案中有2024个基本图形,求n的值.19. 消防车是灭火救灾的主要装备.如图1是一辆登高云梯消防车的实物图,图2是其工作示意图.当云梯升起时,与底盘的夹角为α,液压杆与底盘的夹角为β.已知液压杆m,当 , 时,求的长.(结果精确到m,参考数据: , , )
(1)、写出第5个图案中基本图形的个数:=;(2)、如果第n个图案中有2024个基本图形,求n的值.19. 消防车是灭火救灾的主要装备.如图1是一辆登高云梯消防车的实物图,图2是其工作示意图.当云梯升起时,与底盘的夹角为α,液压杆与底盘的夹角为β.已知液压杆m,当 , 时,求的长.(结果精确到m,参考数据: , , )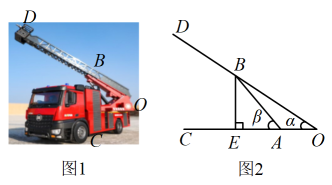 20. 如图,为的直径,半径 , 的切线交的延长线于点E,的弦与相交于点F.
20. 如图,为的直径,半径 , 的切线交的延长线于点E,的弦与相交于点F. (1)、求证:;(2)、若 , 且B为的中点,求的半径长.21. 每年的4月15日是我国全民国家安全教育日.某校开展了“国家安全法”知识竞赛,现从七、八年级学生中各抽取50名学生的竞赛成绩进行统计分析,相关数据整理如下.
(1)、求证:;(2)、若 , 且B为的中点,求的半径长.21. 每年的4月15日是我国全民国家安全教育日.某校开展了“国家安全法”知识竞赛,现从七、八年级学生中各抽取50名学生的竞赛成绩进行统计分析,相关数据整理如下.
平均数(分)
中位数(分)
众数(分)
七年级
80.8
a
70
八年级
b
80
c
请根据以上信息,解答下列问题:
(1)、填空: , , ;(2)、估计该校七、八年级共600名学生中竞赛成绩达到90分及以上的人数;(3)、请你对两个年级学生的“国家安全法”知识竞赛成绩作出评价(从“平均数”“中位数”或“众数”中的一个方面评价即可).22. 如图1,在和中, , . (1)、①求证:;
(1)、①求证:;②若 , 试判断的形状,并说明理由;
(2)、如图2,旋转 , 使点D落在边BC上,若 , . 求证: .23. 如图1,灌溉车沿着平行于绿化带底部边线的方向行驶,为绿化带浇水.喷水口H离地竖直高度为hm,如图2,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象,把绿化带横截面抽象为矩形 . 下边缘抛物线是由上边缘抛物线向左平移得到的,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到绿化带的距离为d m.当m,m,m时,解答下列问题: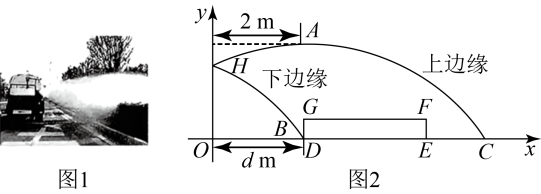 (1)、①求上边缘抛物线的函数解析式,并求喷出水的最大射程;
(1)、①求上边缘抛物线的函数解析式,并求喷出水的最大射程;②求出点B的坐标;
(2)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带,试求出d的取值范围.