山西省阳泉市盂县2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-04-24 类型:期中考试
一、单选题
-
1. 下列图形中,能将其中一个图形平移得到另一个图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 中新社北京时间2021年4月9日7时1分,中国在太原卫星发射中心用长征四号乙运载火箭,成功将试验六号03星发射升空,卫星顺利进入预定轨道.本发火箭是2021年度太原卫星发射中心的首次宇航发射,也是长四型号时隔近半年再次进入太原卫星发射中心执行发射任务.下列表述,能确定太原位置的是( )A、晋中盆地北部地区 B、华北地区黄河流域中部 C、东经 D、东经 ,北纬3. 在我们常见的英文字母中,也存在着同位角、内错角,在下面几个字母中,含有内错角最少的字母是( )A、
2. 中新社北京时间2021年4月9日7时1分,中国在太原卫星发射中心用长征四号乙运载火箭,成功将试验六号03星发射升空,卫星顺利进入预定轨道.本发火箭是2021年度太原卫星发射中心的首次宇航发射,也是长四型号时隔近半年再次进入太原卫星发射中心执行发射任务.下列表述,能确定太原位置的是( )A、晋中盆地北部地区 B、华北地区黄河流域中部 C、东经 D、东经 ,北纬3. 在我们常见的英文字母中,也存在着同位角、内错角,在下面几个字母中,含有内错角最少的字母是( )A、 B、
B、 C、
C、 D、
D、 4. 下列说法中正确的( ).A、2022的相反数表示为 B、9的算术平方根表示为 C、的绝对值表示为 D、16的立方根表示为5. 如图所示是平面直角坐标系的是( )A、
4. 下列说法中正确的( ).A、2022的相反数表示为 B、9的算术平方根表示为 C、的绝对值表示为 D、16的立方根表示为5. 如图所示是平面直角坐标系的是( )A、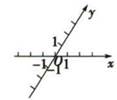 B、
B、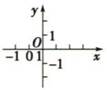 C、
C、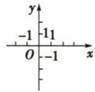 D、
D、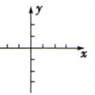 6. 我们在解二元一次方程组时,可将第二个方程代入第一个方程消去得从而求解,这种解法体现的数学思想是( )A、转化思想 B、分类讨论思想 C、数形结合思想 D、公理化思想7. 有一个数值转换器,流程如下:
6. 我们在解二元一次方程组时,可将第二个方程代入第一个方程消去得从而求解,这种解法体现的数学思想是( )A、转化思想 B、分类讨论思想 C、数形结合思想 D、公理化思想7. 有一个数值转换器,流程如下: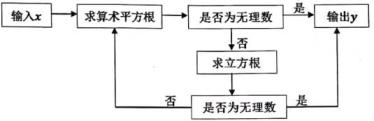
当输入x的值为64时,输出y的值是( )
A、2 B、2 C、 D、8. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( ).A、 , 的补角 , B、 , 的补角 , C、 , 的补角 , D、两个角互为邻补角9. 我国古典文学名著《西游记》讲述了孙悟空、猪八戒、沙和尚保护唐僧西天取经,沿途降妖除魔,历经九九八十一难,到达西天取得真经修成正果的故事.现请你欣赏下列描述孙悟空追妖精的数学诗:悟空顺风探妖踪,千里只行四分钟,归时四分行六百,风速多少才称雄?解释:孙悟空顺风去查妖精的行踪,4分钟就飞跃1000里,逆风返回时4分钟走了600里,问风速是多少?( ).A、50里/分 B、150里/分 C、200里/分 D、250里/分10. 定义:平面内的直线与相交于点O,对于该平面内任意一点M,点M到直线、的距离分别为a、b,则称有序非负实数对是点M的“距离坐标”,根据上述定义,“距离坐标”为的点的个数有( ). A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 平方根节是数学爱好者的节日,这一天的月份和日期的数字正好是当年年份最后两位数字的平方根,例如2009年的3月3日。请你写出本世纪内你喜欢的一个平方根节(题中所举例子除外):年月日.12. 我们知道:有顺序的两个实数a、b组成的数对,叫做有序数对.如果从2,8,5三个数中任选两个组成有序数对,一共可以组成有序数对有对.13. 根据以下对话,可以求得嫒嫒所买的笔和笔记本的价格分别是 .
 14. 一副三角尺ABC,DEF拼接成如图所示的图形,其中∠B=30°,∠D=45°,DF经过点A,两斜边AB与DE互相平行,则∠CAF=度.
14. 一副三角尺ABC,DEF拼接成如图所示的图形,其中∠B=30°,∠D=45°,DF经过点A,两斜边AB与DE互相平行,则∠CAF=度. 15. 数学课上,老师出示关于x,y的方程组 , 让学生以小组形式展开讨论.展示环节有下列结论:①当时,方程组的解是;②当x,y的值互为相反数时,;③不存在一个实数a使得;④若 , 则 . 上述结论中正确的个数有个.
15. 数学课上,老师出示关于x,y的方程组 , 让学生以小组形式展开讨论.展示环节有下列结论:①当时,方程组的解是;②当x,y的值互为相反数时,;③不存在一个实数a使得;④若 , 则 . 上述结论中正确的个数有个.三、解答题
-
16.(1)、计算:;(2)、以下是小凡同学用代入法解方程组的解答过程:
解:由①得③; 第一步
把③代入②得; 第二步
去分母得; 第三步
解之得 , 再由③得 . 第四步
①填空:以上解题过程中,第 ▲ 步开始出现错误,这一步错误的原因是 ▲ ;请直接写出方程组的解 ▲ ;
②请你根据平时的学习经验,就解二元一次方程组要注意的事项给其他同学提一条建议.
17. 把下列各数填入相应的集合中:, , 7,0, , , …(每两个1之间多一个2), ,
无理数集合:{ ……};
负有理数集合:{ ……}
{ ……}.
18. 如图,已知 , ,求证: . 19. 如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
19. 如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3). (1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请把△ABC先向右平移5个单位,再向下平移3个单位得到△A′B′C′,在图中画出△A′B′C′,并写出点B的对应点B′的坐标;(3)、求△ABC的面积.20. 如图,直线、相交于点 , .
(1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请把△ABC先向右平移5个单位,再向下平移3个单位得到△A′B′C′,在图中画出△A′B′C′,并写出点B的对应点B′的坐标;(3)、求△ABC的面积.20. 如图,直线、相交于点 , . (1)、的余角是(填写所有符合要求的角).(2)、若 , 求的度数.(3)、若 , 求的度数.21. 阅读材料,完成下列任务:
(1)、的余角是(填写所有符合要求的角).(2)、若 , 求的度数.(3)、若 , 求的度数.21. 阅读材料,完成下列任务:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来比如:、等,而常用的“…”或者“≈”的表示方法都不够百分百准确.
材料一:∵ , 即 ,
∴ .
∴的整数部分为1.
∴的小数部分为 .
材料二:我们还可以用以下方法求一个无理数的近似值.
我们知道面积是2的正方形的边长是 , 易知 , 因此可设 , 可画出如图示意图.由图中面积计算, , 另一方面由题意知 , 所以 .
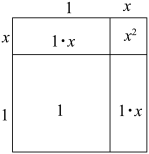
略去 , 得方程 , 解得 , 即 .
解决问题:
(1)、利用材料一中的方法,求的小数部分;(2)、利用材料二中的方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)22.(1)、问题发现:如图 1,已知点 F,G 分别在直线 AB,CD 上,且 AB∥CD,若∠BFE=40°,∠CGE=130°,则∠GEF 的度数为; (2)、拓展探究:∠GEF,∠BFE,∠CGE 之间有怎样的数量关系?写出结论并给出证明; 答:∠GEF= ▲ .
(2)、拓展探究:∠GEF,∠BFE,∠CGE 之间有怎样的数量关系?写出结论并给出证明; 答:∠GEF= ▲ .证明:过点 E 作 EH∥AB,

∴∠FEH=∠BFE( ),
∵AB∥CD,EH∥AB,(辅助线的作法)
∴EH∥CD( ),
∴∠HEG=180°-∠CGE( ),
∴∠FEG=∠HFG+∠FEH= ▲ .
(3)、深入探究:如图 2,∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P,试探究∠GPQ 与∠GEF 之间的数量关系,请直接写出你的结论. 23. 在平面直角坐标系中 单位长度为 ,已知 , ,其中a,b满足 .(1)、填空: , ;(2)、若点E是第一象限内一点,且 轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A.点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
23. 在平面直角坐标系中 单位长度为 ,已知 , ,其中a,b满足 .(1)、填空: , ;(2)、若点E是第一象限内一点,且 轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A.点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
①经过几秒PQ平行于y轴?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是 ,求此时点P的坐标.