山西省吕梁市交口县2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-04-24 类型:期中考试
一、单选题
-
1. 有理数-2021的倒数是( )A、 B、 C、2021 D、2. 在有理数、、、、负数有( )个A、4 B、3 C、2 D、13. 截至北京时间2021年12月22日6时30分左右,全球因感染新冠肺炎而死亡的病例约5380000例,携手抗“疫”,刻不容缓.数据5380000可以用科学记数法表示为( )A、 B、 C、 D、4. 下列计算中正确的是( )A、 B、 C、 D、3x2+2x3=5x55. 下图是由八个相同的小正方体组合而成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 将方程去分母得到 , 错在( )A、分母的最小公倍数找错 B、去分母时,漏乘了分母为1的项 C、去分母时,分子部分没有加括号 D、去分母时,各项所乘的数为各分母的最小公倍数127. 若数 , 在数轴上的位置如图所示,则下列式子正确的是( )
6. 将方程去分母得到 , 错在( )A、分母的最小公倍数找错 B、去分母时,漏乘了分母为1的项 C、去分母时,分子部分没有加括号 D、去分母时,各项所乘的数为各分母的最小公倍数127. 若数 , 在数轴上的位置如图所示,则下列式子正确的是( ) A、 B、 C、 D、8. 如图,将一副三角尺按不同位置摆放,下列选项的摆放方式中∠1与∠2互余的是( )A、
A、 B、 C、 D、8. 如图,将一副三角尺按不同位置摆放,下列选项的摆放方式中∠1与∠2互余的是( )A、 B、
B、 C、
C、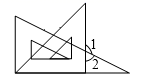 D、
D、 9. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示方法,观察图①,可推算图②所得到的数值为( )
9. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示方法,观察图①,可推算图②所得到的数值为( )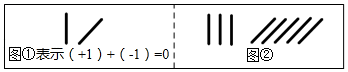 A、2 B、﹣2 C、8 D、﹣810. 如图,甲,乙两人同时从A地出发,沿图示方向分别步行前进到B,C两地,现测得为100°,B地位于A地的北偏东50°方向,则C地位于A地的( )
A、2 B、﹣2 C、8 D、﹣810. 如图,甲,乙两人同时从A地出发,沿图示方向分别步行前进到B,C两地,现测得为100°,B地位于A地的北偏东50°方向,则C地位于A地的( ) A、北偏西50°方向 B、北偏西30°方向 C、南偏东50°方向 D、南偏东30°方向
A、北偏西50°方向 B、北偏西30°方向 C、南偏东50°方向 D、南偏东30°方向二、填空题
-
11. 单项式 的次数是次.12. 如图,从点A到B有a、b、c三条通道,最近的一条通道是b,这是因为 .
 13. 如图,点 , 是线段上的两点, , , 点为线段的中点,则线段的长为 .
13. 如图,点 , 是线段上的两点, , , 点为线段的中点,则线段的长为 . 14. 若x=3是关于的方程4x+a=ax的解,则a的值为 .15. 用火柴棒搭成如图所示的图形,第①个图形需要3根火柴棒,第②个图形需要5根火柴棒…,用同样方式,第n个图形需根火柴棒(用含n的代数式表示).
14. 若x=3是关于的方程4x+a=ax的解,则a的值为 .15. 用火柴棒搭成如图所示的图形,第①个图形需要3根火柴棒,第②个图形需要5根火柴棒…,用同样方式,第n个图形需根火柴棒(用含n的代数式表示).
三、解答题
-
16. 计算:(1)、;(2)、 .17. 解方程:(1)、 ;(2)、 .18. 已知:A=2x2+3xy﹣2x﹣1,B=﹣x2﹣xy+1.(1)、求3A+6B的值;(2)、若(1)中的值与x的值无关,试求y的值.19. 阅读材料:对于任何数,我们规定符号的意义是 , 例如: .(1)、按照这个规定,请你计算的值;(2)、按照这个规定,请你计算当时,的值.20. 某商场从厂家购进了 、 两种品牌足球共100个已知购买 品牌足球比购买 品牌足球少花2800元,其中 品牌足球每个进价是50元, 品牌足球每个进价是80元.(1)、求购进 、 两种品牌足球各多少个?(2)、在销售过程中, 品牌足球每个售价是80元很快全部售出; 品牌足球每个按进价加价25%销售,售出一部分后,出现滞销,商场决定打九折出售剩余的 品牌足球,两种品牌足球全部售出后共获利2200元,有多少个 品牌足球打九折出售?21. 某班计划买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价100元,乒乓球每盒定价25元.经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不少于5盒).问:(1)、当购买乒乓球多少盒时,两种优惠办法付款一样?(2)、当购买20盒、40盒乒乓球时,去哪家商店购买更合算?22. 观察下列三行数:
, 4, , 16, , 64,…;①
, 5, , 17, , 65,…;②
, 2, , 8, , 32…;③
(1)、第三行的第个数为;(2)、如图1,在上面的数据中,用一个矩形方框框住同一列的三个数,设 , 则(用含的式子表示); (3)、如图2,在上面的数据中,用一个矩形方框框住两列共六个数,数 , , 为第列的三个数,若方框中的六个数之和为 , 求的值.
(3)、如图2,在上面的数据中,用一个矩形方框框住两列共六个数,数 , , 为第列的三个数,若方框中的六个数之和为 , 求的值. 23. 综合与探究:
23. 综合与探究: (1)、(问题探究)
(1)、(问题探究)如图①,点C是线段AB上一点,点D,E分别是线段AC,BC的中点,若线段 , 求:线段DE的长.
(2)、(拓展应用)①如图②, , 点C在内部,射线OM,ON分别平分 , , 求的大小.
②如图③,在(1)中,若点C在外部,且射线OC与射线OB在OA所在直线的同侧,其他条件不变,则(1)中的结论是否成立,若成立,请写出求解过程;若不成立,请说明理由.