山西省晋中市介休市2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-04-24 类型:期中考试
一、单选题
-
1. 下列计算结果是 的为( )A、 B、 C、 D、2. 如图,下列各组角中,互为内错角的是( )
 A、和 B、和 C、和 D、和3. 当时,下列关于幂的运算正确的是( )A、 B、 C、 D、4. 如图所示,某同学的家在处,他想尽快赶到附近公路边搭公交车,他选择路线,用几何知识解释其道理正确的是( )
A、和 B、和 C、和 D、和3. 当时,下列关于幂的运算正确的是( )A、 B、 C、 D、4. 如图所示,某同学的家在处,他想尽快赶到附近公路边搭公交车,他选择路线,用几何知识解释其道理正确的是( ) A、两点之间线段最短 B、经过两点有且只有一条直线 C、两点确定一条直线 D、垂线段最短5. 2021年12月9日“天宫课堂”开讲,神舟十三号飞行乘组航天员翟志刚、王亚平、叶光富演示了微重力环境下细胞学实验、人体运动、液体表面张力等神奇现象.细胞的大小依据细胞种类不同有很大的差异,目前已知最小的细胞是支原体,直径只有0.1-0.3μm.已知1μm=0.000001m,则0.3μm用科学记数法可以表示为( )
A、两点之间线段最短 B、经过两点有且只有一条直线 C、两点确定一条直线 D、垂线段最短5. 2021年12月9日“天宫课堂”开讲,神舟十三号飞行乘组航天员翟志刚、王亚平、叶光富演示了微重力环境下细胞学实验、人体运动、液体表面张力等神奇现象.细胞的大小依据细胞种类不同有很大的差异,目前已知最小的细胞是支原体,直径只有0.1-0.3μm.已知1μm=0.000001m,则0.3μm用科学记数法可以表示为( ) A、 B、 C、 D、6. 你能根据下图中图形的面积关系得到的数学公式是( )
A、 B、 C、 D、6. 你能根据下图中图形的面积关系得到的数学公式是( ) A、 B、 C、 D、7. 如图,点E、F分别在线段AB和CD上,下列条件中能判定的是( )
A、 B、 C、 D、7. 如图,点E、F分别在线段AB和CD上,下列条件中能判定的是( ) A、 B、 C、 D、8. 随着我国经济的发展,国民生活水平的提高,车辆数目也在不断增加,老式街道由于宽度和承载能力有限,制约了城市交通的发展速度,因而急需对原有的老式道路进行扩宽改造.某市对一道路进行拓宽改造,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路y(米)与时间x(天)的关系的大致图象是( )
A、 B、 C、 D、8. 随着我国经济的发展,国民生活水平的提高,车辆数目也在不断增加,老式街道由于宽度和承载能力有限,制约了城市交通的发展速度,因而急需对原有的老式道路进行扩宽改造.某市对一道路进行拓宽改造,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路y(米)与时间x(天)的关系的大致图象是( ) A、
A、 B、
B、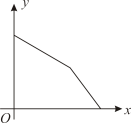 C、
C、 D、
D、
二、填空题
-
9. 计算:(x+1)(x+2)= .10. 如图1,是一把剪刀,图2,是其示意图,若 , 则的度数是 .
 11. 科技小制作的特点在于富含科技,结构简单、材料好找、加工容易、能够独立完成,特别适合于学生.如图所示,某科技制作小组制作的一艘航模船从A点出发,沿东北方向航行至B点,再从B点出发沿南偏东15°方向航行至C点,则等于 .
11. 科技小制作的特点在于富含科技,结构简单、材料好找、加工容易、能够独立完成,特别适合于学生.如图所示,某科技制作小组制作的一艘航模船从A点出发,沿东北方向航行至B点,再从B点出发沿南偏东15°方向航行至C点,则等于 .
三、解答题
-
12. 计算:(1)、(2)、13.(1)、化简:(2)、阅读下面这位同学的计算过程,并完成任务
先化简,再求值: , 其中 , .
解:原式 第一步
第二步
. 第三步
当 , 时,原式 . 第四步
任务:
①第一步运算用到了乘法公式 ▲ (写出1种即可);
②以上步骤第 ▲ 步出现了错误,错误的原因是 ▲ ;
③请写出正确的解答过程.
14. 阅读下列推理过程,并完成任务:已知:如图, , , CE平分 , , . 求的度数.

解:因为 ① .所以(依据1).
因为 , 所以 .
因为 , 所以 .
因为CE平分 , 所以 .
因为 , , 所以(依据2).
所以 ② .
任务:
(1)、将上述推理过程补充完整.①:②:
(2)、上述解答过程中的“依据1”“依据2”分别指什么?“依据1”: .
“依据2”: .
15. 一根原长为20cm的蜡烛,点燃后,其剩余长度与燃烧时间之间的关系可以从下面的表格看出:燃烧时间t(min)
10
20
30
40
50
…
剩余长度y(cm)
19
18
17
16
15
…
(1)、在这个变化过程中,自变量是因变量是;(2)、每分钟蜡烛燃烧的长度为cm;用关系式表示上表中两个变量之间的关系为;(3)、估计这根蜡烛最多可燃烧分钟.16. 作图题:如图,点 , 均在直线上,.
( 1 )在图中作 , 使(保留作图痕迹,不写作法).
( 2 )请直接说出直线与直线的位置关系.
17. 风是地球上的一种空气流动现象,一般是由太阳辐射热引起的.风的测量多用电接风向风速计、轻便风速表、达因式风向风速计,以及用于测量农田中微风的热球微风仪等仪器进行.小力同学使用轻便风速表观测了某天连续12个小时风力变化的情况,并绘制下图 (1)、上图反映了哪两个变量之间的关系?自变量是什么?因变量是什么?(2)、A,B两点表示什么?(3)、什么时间范围内风力最大?此时风力为多少?(4)、简要描述8—12时风力变化的情况.18. 数形结合是一种非常重要的数学思想,它包含两个方面,第一种是“以数解形”,第二种是“以形助数”,我国著名数学家华罗庚曾说过:“数无形时少直觉,形少数时难入微”.请你使用数形结合这种思想解决下面问题:
(1)、上图反映了哪两个变量之间的关系?自变量是什么?因变量是什么?(2)、A,B两点表示什么?(3)、什么时间范围内风力最大?此时风力为多少?(4)、简要描述8—12时风力变化的情况.18. 数形结合是一种非常重要的数学思想,它包含两个方面,第一种是“以数解形”,第二种是“以形助数”,我国著名数学家华罗庚曾说过:“数无形时少直觉,形少数时难入微”.请你使用数形结合这种思想解决下面问题:图1是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分为四块完成相同的小长方形,然后按照图2的形状拼成一个正方形.
 (1)、观察图2,用两种方法计算阴影部分的面积,可以得到一个等式,请使用代数式 , , ab写出这个等式 .
(1)、观察图2,用两种方法计算阴影部分的面积,可以得到一个等式,请使用代数式 , , ab写出这个等式 . (2)、运用你所得到的公式,计算:若m、n为实数,且 , , 试求的值.(3)、如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设 , 两正方形的面积和 , 求图中阴影部分的面积.
(2)、运用你所得到的公式,计算:若m、n为实数,且 , , 试求的值.(3)、如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设 , 两正方形的面积和 , 求图中阴影部分的面积. 19. 综合与实践:
19. 综合与实践:问题情境:在综合与实践课上,同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动.如图1,已知两直线a,b且和直角三角形ABC, , , .
(1)、操作发现:在图1中, , 求的度数;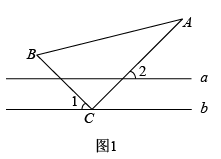 (2)、如图2,创新小组的同学把直线a向上平移,并把的位置改变,发现 , 说明理由;
(2)、如图2,创新小组的同学把直线a向上平移,并把的位置改变,发现 , 说明理由; (3)、实践探究:缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,AC平分 , 此时发现与又存在新的数量关系,请写出你的发现并说明理由.
(3)、实践探究:缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,AC平分 , 此时发现与又存在新的数量关系,请写出你的发现并说明理由.