2022-2023学年浙教版数学八年级下册第五章 特殊平行四边形 综合测试
试卷更新日期：2023-04-23 类型：单元试卷
一、单选题
-
1. 在矩形中， ， 对角线交于点O，则（ ）
A、3 B、4 C、5 D、102. 如图，将矩形ABCD沿直线DE折叠，顶点A落在BC边上F处，已知 ， ， 则BF的长为（ ）
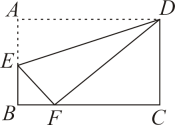A、5 B、4 C、3 D、23. 下列说法正确的是（ ）A、三条边相等的四边形是菱形 B、对角线相等的平行四边形是矩形 C、连接矩形各边中点所得四边形是正方形 D、一组对边平行，另一组对边相等的四边形是平行四边形4. 如图，已知四边形是平行四边形，下列结论中正确的是（ ）
A、当时，它是矩形 B、当时，它是矩形 C、当时，它是正方形 D、当时，它是菱形5. 如图，在菱形ABCD中，对角线AC、BD相交于点O，BE⊥AD于点E，且 ， ． 则BE的长为（ ）
A、3 B、4 C、4.8 D、56. 在一组对边平行的四边形中，增加一个条件，使得这个四边形是菱形，那么增加的条件可以是（ ）A、另一组对边相等，对角线相等 B、另一组对边相等，对角线互相垂直 C、另一组对边平行，对角线相等 D、另一组对边平行，对角线相互垂直7. 如图，菱形ABCD的对角线相交于点O，E是CD的中点，且OE＝3，则菱形的周长是（ ）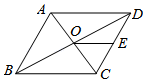
A、12 B、16 C、20 D、248. 如图，在矩形中， ， 以点B为圆心，长为半径画弧，交边于点E，则的长为（ ）
A、9 B、8 C、7 D、69. 如图，正方形中，点为对角线的交点，直线过点分别交 ， 于 ， 两点（），若过点作直线与正方形的一组对边分别交于 ， 两点，满足 ， 则这样的直线（不同于直线）的条数共有（ ）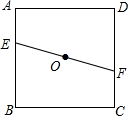
A、1条 B、2条 C、3条 D、无数条10. 如图，在正方形中，将边绕点B逆时针旋转至 ， 连接 ， ， 若 ， ， 则线段的长度为（ ）
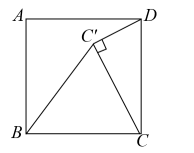A、 B、 C、 D、3二、填空题
-
11. 一个木匠要制作矩形的踏板．他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次，就能得到矩形踏板．理由是 ．
12. 如图，O是矩形ABCD对角线AC的中点，E是AB上的一点，将沿CE折叠后，点B恰好与点O重合．若 ， 则折痕CE的长为 ．
13. 如图，在四边形ABCD中，P、Q、M、N分别是AD、BC、BD、AC的中点，当四边形ABCD满足时（填写一个条件），PQ⊥MN.
14. 如图，菱形ABCD中，对角线AC、BD相交于点O，点E为AC上一点，连接DE，AB＝CE＝5AE，BD＝8，则DE的长为 ．
15. 如图，在矩形ABCD中， ， ， 点P从点A向点D以每秒1cm的速度运动，Q以每秒4cm的速度从点C出发，在B、C两点之间做往返运动，两点同时出发，点P到达点D为止(同时点Q也停止)，这段时间内，当运动时间为时，P、Q、C、D四点组成矩形．
16. “勾股图”有着悠久的历史，欧几里得在《几何原本》中曾对它做了深入研究.如图，在△ABC中，∠ACB＝90°，分别以△ABC的三条边为边向外作正方形.连接EB，CM，DG，CM分别与AB，BE相交于点P，Q.若∠AMP＝30°，则∠ABE＝°，的值为 .
三、解答题
-
17. 如图，菱形ABCD中，点E、F分别是边CD、AD的中点．求证： ．
18. 已知四边形ABCD，// ， AD=DC=10，DB平分∠ADC，BD=12，求四边形ABCD的面积．
19. 如图，在菱形中，对角线与相交于点 ， 为的中点，过点作交的延长线于点 ， 连接 ． 求证：四边形是矩形．
20. 如图，菱形的对角线相交于点O，垂直平分 ， 垂足为点E，求的大小．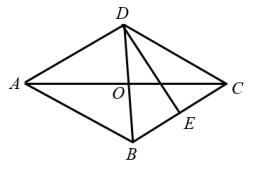
21. 只用无刻度的直尺作图（保留作图痕迹，不要求写作法）．如图，已知 ， ， 点E在OB边上，其中四边形AEBF是平行四边形，
(1)、请在图中画出的平分线．(2)、请在图中画出菱形AOBN．22. 如图，矩形ABCD的对角线AC，BD相交于点O，且DE∥AC，CE∥BD．试判断四边形OCED的形状并证明．
23. 如，在矩形ABCD中，AB=16 cm，AD=6 cm，动点P，Q分别从点A，C同时出发，点P以每秒3 cm的速度向点B移动，点Q以每秒2 cm的速度向点D移动，当点P到达点B时，两点均停止移动.是否存在某一时刻，使四边形PBCQ为正方形?若存在，求出该时刻；若不存在，请说明理由.
24. 如图1，点C在线段AB上，分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN，连结AM、BD．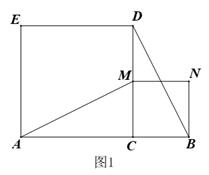
(1)、AM与BD的关系是： ．(2)、如果将正方形BCMN绕点C顺时针旋转锐角α，它不变（如图2）．（1）中所得的结论是否仍然成立？请说明理由．
(3)、在（2）的条件下，连接AB、DM，若AC＝4，BC＝2，求 的值．