2022-2023学年浙教版数学八年级下册第六章反比例函数综合测试

试卷更新日期：2023-04-23 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列函数中，表示y是x的反比例函数的是（）

A、 $y = \sqrt{3} x$ B、 $y = \frac{a}{x}$ C、 $y = \frac{1}{x^{2}}$ D、 $y = \frac{1}{3 x}$

查看试题解析
2. 已知 $y$ 与 $x$ 成反比例，且 $x = 2$ 时， $y = 3$ ，则 $y$ 关于 $x$ 的函数表达式是（）

A、 $y = 6 x$ B、 $y = \frac{1}{6 x}$ C、 $y = \frac{6}{x}$ D、 $y = \frac{6}{x^{- 1}}$

查看试题解析
3. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ ，当自变量 $x$ 的值从3增加到6时，函数值减少了1，则函数的表达式为（）

A、 $y = \frac{6}{x}$ B、 $y = \frac{3}{x}$ C、 $y = \frac{2}{x}$ D、 $y = \frac{1}{2 x}$

查看试题解析
4. 已知 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ 是反比例函数 $y = - \frac{4}{x}$ 图象上的三个点，且 $x_{1} < 0 < x_{2} < x_{3}$ ，那么 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{3} > y_{2} > y_{1}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{2} > y_{3} > y_{1}$

查看试题解析
5. 若反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = x + 2$ 的图象没有交点，则 $k$ 的值可以是（）

A、-2 B、-1 C、1 D、2

查看试题解析
6.
如图，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象与一次函数y=ax+b的图象交于点A（1，6）和点B（3，2）．当ax+b＜ $\frac{k}{x}$ 时，则x的取值范围是（　　）

A、1＜x＜3 B、x＜1或x＞3 C、0＜x＜1 D、0＜x＜1或x＞3

查看试题解析
7. 已知一次函数 $y_{1} = a x + b$ 与反比例函数 $y_{2} = \frac{k}{x} (x$ $> 0)$ 的图象如图所示，当 $y_{1} < y_{2}$ 时， $x$ 的取值范围是（）

A、 $x < 2$ B、 $0 < x < 2$ 或 $x > 5$ C、 $2 < x < 5$ D、 $x > 5$

查看试题解析
8. 要确定方程 $x^{2} + x - 5 = 0$ 的解，只需知道一次函数 $y = x + 1$ 和反比例函数 $y = \frac{k}{x}$ 的图象交点的横坐标．由上面的信息可知， $k$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
9. 如图，点A在x轴正半轴上，点B在第二象限内，直线AB交y轴于点F， $B C ⊥ x$ 轴，垂足是C，反比例函数 $y = \frac{k}{x}$ 的图象分别交BC，AB于点 $D (- 4 ， 1)$ ， E，若 $A F = E F = B E$ ，则△ABC的面积为（）

A、 $\frac{15}{2}$ B、8 C、9 D、10

查看试题解析
10. 某品牌的饮水机接通电源就进入自动程序：开机加热到水温100℃，停止加热，水温开始下降，此时水温y(℃)与开机后用时.x(min)成反比例关系，直至水温降至30℃，饮水机关机.饮水机关机后即刻自动开机，重复上述自动程序.若在水温为30℃时，接通电源后，水温y(℃)和时间x(min)的关系如图所示，水温从100℃降到35℃所用的时间是（）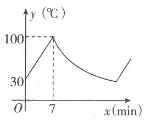

A、27min B、20min C、13min D、7min

查看试题解析

二、填空题（每空4分，共24分）

11. 反比例函数 $y = \frac{1}{2 x}$ 的比例系数是．

查看试题解析
12. 若 $y = \frac{m - 1}{x^{| m |}}$ 是反比例函数，则m的值为；

查看试题解析
13. 已知双曲线 $y = \frac{k}{x}$ 经过点（2，-3），则k的值是.

查看试题解析
14. 如图，点A在双曲线y= $\frac{k}{x}$ 上，AB⊥y轴于B，S_△_ABO =3，则k=

查看试题解析
15. 若点 $A (- 1 ， y_{1}) ， B (2 ， y_{2})$ 在反比例函数 $y = - \frac{6}{x}$ 的图象上，则 $y_{1} ， y_{2}$ 的大小关系是．

查看试题解析
16. 在同一平面直角坐标系中，正比例函数y＝k₁x的图象与反比例函数y $= \frac{k_{2}}{x}$ 的图象一个交点的坐标是（-2，3），则它们另一个交点的坐标是.

查看试题解析

三、解答题（共8题，46分）

17. 已知y=y₁+y₂ ， y₁与x成正比例，y₂与x+2成反比例，且当x=﹣1时，y=3；当x=3时，y=7．求x=﹣3时，y的值．

查看试题解析
18. 已知反比例函数 $y = \frac{m - 5}{x}$ 的图象过点P（－1，3），求m的值和该反比例函数的表达式.

查看试题解析
19. 已知点p（m，n）是反比例函数 $y = \frac{2}{x}$ 图象上一动点，且m≠n，将代数式 $(\frac{1}{m - n} + \frac{1}{m + n}) \div \frac{m^{2} n}{m^{2} - n^{2}}$ 化简并求值.

查看试题解析
20. 已知一次函数 $y = k x + b$ 与反比例函数 $y = \frac{m}{x}$ 的图象交于P（2，a）和Q（﹣1，﹣4），求这两个函数的解析式.

查看试题解析
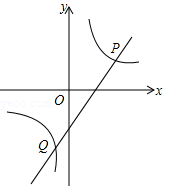21. 甲工程队新建公路，每名工人每天工作8小时，则甲工程队每天可完成600米新建公路．乙工程队比甲工程队少10名工人，每名工人每天工作10小时，则乙工程队每天可完成500米新建公路，假定甲、乙两工程队的每名工人每小时完成的工作量相同，求乙工程队的工人有多少名？

查看试题解析
22. 已知：如图所示，反比例函数 $y = \frac{k}{x}$ 的图象与正比例函数 $y = m x$ 的图象交于A、B，作AC⊥ $y$ 轴于C，连BC，则△ABC的面积为3，求反比例函数的解析式．

查看试题解析
23. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于 $A (- 2 ， 1)$ ， $B (1 ， n)$ 两点.

$($ Ⅰ $)$ 试确定上述反比例函数和一次函数的表达式；

$($ Ⅱ $)$ 连OB，在x轴上取点C，使 $B C = B O$ ，并求 $△ O B C$ 的面积；

$($ Ⅲ $)$ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.

查看试题解析
24. 平面直角坐标系中，反比例函数 $y = \frac{3 k}{x} (k \neq 0)$ 的图象与一次函数 $y = k x - 2 k$ 图象交于A、B两点（点A在点B左侧）.

(1)、求A、B两点的坐标（用含k的代数式表示）；

(2)、当 $k = 2$ 时，过y轴正半轴上一动点 $C (0 ， n)$ 作平行于x轴的直线，分别与一次函数 $y = k x - 2 k$ 、反比例函数 $y = \frac{3 k}{x}$ 的图象相交于D、E两点，若 $C D = 3 D E$ ，求n的值；

(3)、若一次函数 $y = k x - 2 k$ 图象与x轴交于点F， $A F + B F \leq 5$ ，直接写出k的取值范围.

查看试题解析

2022-2023学年浙教版数学八年级下册第六章 反比例函数 综合测试

一、单选题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，46分）

2022-2023学年浙教版数学八年级下册第六章反比例函数综合测试