浙江省湖州市吴兴区2022-2023学年八年级下学期数学期中试题

试卷更新日期：2023-04-23 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30分)

1. 若x为任意实数，下列各式一定是二次根式的是（）

A、 $\sqrt{x^{2} - 3}$ B、 $\sqrt{\frac{2}{{(x + 1)}^{2}}}$ C、 $\sqrt{x^{2} + 1}$ D、 $\sqrt{x^{2} + 2 x}$

查看试题解析
2. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
3. 如图，在平行四边形ABCD中，∠A：∠B＝7：2，则∠A的度数是（）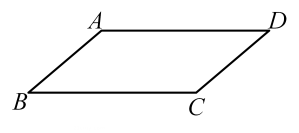

A、110° B、140° C、120° D、160°

查看试题解析
4. 下列根式中，不是最简二次根式的是（）

A、 $\sqrt{5}$ B、 $\sqrt{8}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\sqrt{6}$

查看试题解析
5. 有一组数据： $2$ ， $5$ ， $5$ ， $6$ ， $7$ ，这组数据的平均数为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
6. 用配方法解一元二次方程 $x^{2} - 2 x - 5 = 0$ 时，可配方得（）

A、 $(x - 1)^{2} = 6$ B、 $(x + 2)^{2} = 9$ C、 $(x + 1)^{2} = 6$ D、 $(x - 2)^{2} = 9$

查看试题解析
7. 用反证法证明命题：“等腰三角形的底角是锐角”时，第一步可以假设（）

A、等腰三角形的底角是直角 B、等腰三角形的底角是直角或钝角 C、等腰三角形的底角是钝角 D、底角为锐角的三角形是等腰三角形

查看试题解析
8. 若m是关于x的方程x²-2023x-1＝0的根，则（m²-2023m+3）•（m²-2023m+4）的值为（）

A、16 B、12 C、20 D、30

查看试题解析
9. 如图，将平行四边形ABCD沿对角线BD折叠，使点A落在E处，若∠1＝56°，∠2＝42°，则∠A的度数为（）

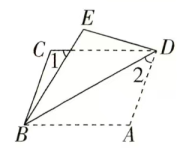A、108° B、109° C、110° D、111°

查看试题解析
10. 如图，在平行四边形ABCD中，点E在边AD上，过E作EF∥CD交对角线AC于点F，若要求△FBC的面积，只需知道下列哪个三角形的面积即可（）

A、△ECD B、△EBF C、△EBC D、△EFC

查看试题解析

二、填空题（本大题共6小题，共24分)

11. 当x=2时，二次根式 $\sqrt{1 + x^{2}}$ 的值是.

查看试题解析
12. 若关于 x的一元二次方程 x²－4x+4=m没有实数根，则 m的取值范围是.

查看试题解析
13. 已知一个多边形的内角和比外角和大180°，则多边形的边数是

查看试题解析
14. 我校八年级组织班级篮球赛，赛制为单循环形式（即每两班之间都比赛一场），若共进行了45场比赛，则有个班级篮球队参加.

查看试题解析
15. 如图，在四边形ABCD中，∠A=90°AB=AD，E、F分别是AB、AD中点，若EF＝ $\sqrt{2}$ ，BC＝ $\sqrt{11}$ ，CD＝ $\sqrt{3}$ ，则S_{四边形ABCD}＝

查看试题解析
16. 在平行四边形ABCD中，AC与BD交于点M，点F在AD上，AF=6cm，BF=12cm，∠FBM=∠CBM，点E是BC的中点，若点P以1cm/秒的速度从点A出发，沿AD向点F运动；点Q同时以2cm/秒的速度从点C出发，沿CB向点B运动．点P运动到F点时停止运动，点Q也同时停止运动．当点P运动秒时，以点P、Q、E、F为顶点的四边形是平行四边形．

查看试题解析

三、解答题（本大题共8小题，共66分.）

17. 计算：

(1)、 $\frac{1}{2} \sqrt{24} - 2 \sqrt{3} \times \sqrt{2}$

(2)、 $(\sqrt{3} + \sqrt{5})_{}^{2} + (\sqrt{3} - 1) (\sqrt{3} + 1)$

查看试题解析
18. 解方程：

(1)、 $x^{2} - x - 1 = 0$

(2)、 $3 x (x - 1) = 2 - 2 x$

查看试题解析
19. 如图，在7×6的正方形网格中，点A，B，C，D都在格点上，请你按要求画出图形．

(1)、在图甲中作出△A₁B₁C₁ ，使△A₁B₁C₁和△ABC关于点D成中心对称；

(2)、在图乙中分别找两个格点C₂、D₂ ，使得以A、B、C₂、D₂为顶点的四边形为平行四边形，并且平行四边形的面积为△ABC面积的4倍．

查看试题解析
20. 八年级学生开展踢毽子比赛，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀，下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：

1号
2号
3号
4号
5号
总数
甲班
89
100
96
118
97
500
乙班
100
95
110
91
104
500
请你回答下列问题：

(1)、甲班的优秀率为40%，乙班的优秀率为；甲班5名学生比赛成绩的中位数是个，乙班5名学生比赛成绩的中位数是100个；

(2)、求两班比赛数据的方差；

(3)、根据以上信息，你认为应该把冠军奖杯发给哪一个班级？简述你的理由．

查看试题解析
21. 如图，平行四边形ABCD中，DE⊥AC，BF⊥AC，垂足分别是E，F．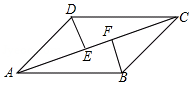

(1)、求证：AE=CF．

(2)、连结EB，DF，若AD=4，AC=7，∠DAC=30°，求四边形DEBF的面积.

查看试题解析
22. 端午节期间，诸老大粽子店平均每天可以卖出300只粽子，卖出1只粽子的利润是1元．经调查发现，零售单价每降0.1元，每天可多卖出100只粽子．为了使每天获取的利润更多，该店决定把零售单价下降m(0<m<1)元．

(1)、零售单价下降0.2元后，该店平均每天可卖出只粽子，利润为元．

(2)、在不考虑其他因素的条件下，当m定为多少时，才能使该店每天获取的利润是420元并且卖出的粽子更多？

查看试题解析
23. 阅读下列材料，解答后面的问题：
在二次根式的学习中，我们不仅要关注二次根式本身的性质、运算，还要用到与分式、不等式相结合的一些运算．如：

①要使二次根式 $\sqrt{a - 2}$ 有意义，则需a-2≥0，解得：a≥2；

②化简： $\sqrt{1 + \frac{1}{n_{}^{2}} + \frac{1}{{(n + 1)}_{}^{2}}}$ ，则需计算 $1 + \frac{1}{n_{}^{2}} + \frac{1}{{(n + 1)}_{}^{2}}$ ，而 $1 + \frac{1}{n_{}^{2}} + \frac{1}{{(n + 1)}_{}^{2}} = \frac{n_{}^{2} {(n + 1)}_{}^{2} + {(n + 1)}_{}^{2} + n_{}^{2}}{n_{}^{2} {(n + 1)}_{}^{2}}$

$= \frac{n_{}^{2} {(n + 1)}_{}^{2} + n_{}^{2} + 2 n + 1 + n_{}^{2}}{n_{}^{2} {(n + 1)}_{}^{2}} = \frac{n_{}^{2} {(n + 1)}_{}^{2} + 2 n_{}^{2} + 2 n + 1}{n_{}^{2} {(n + 1)}_{}^{2}} = \frac{n_{}^{2} {(n + 1)}_{}^{2} + 2 n (n + 1) + 1}{n_{}^{2} {(n + 1)}_{}^{2}} = \frac{[n (n + 1) + 1]_{}^{2}}{n_{}^{2} {(n + 1)}_{}^{2}}$
所以 $\sqrt{1 + \frac{1}{n_{}^{2}} + \frac{1}{{(n + 1)}_{}^{2}}} = \sqrt{\frac{{[n (n + 1) + 1]}_{}^{2}}{n_{}^{2} {(n + 1)}_{}^{2}}} = \frac{n (n + 1) + 1}{n (n + 1)} = 1 + \frac{1}{n (n + 1)} = 1 + \frac{1}{n} - \frac{1}{n + 1}$

(1)、根据二次根式的性质，要使 $\sqrt{\frac{a + 2}{3 - a}} = \frac{\sqrt{a + 2}}{\sqrt{3 - a}}$ 成立，求a的取值范围；

(2)、利用①中的提示，请解答：如果 $b = \sqrt{a - 2} + \sqrt{2 - a} + 1$ ，求a+b的值；

(3)、利用②中的结论，计算： $\sqrt{1 + \frac{1}{1_{}^{2}} + \frac{1}{2_{}^{2}}} + \sqrt{1 + \frac{1}{2_{}^{2}} + \frac{1}{3_{}^{2}}} + \sqrt{1 + \frac{1}{3_{}^{2}} + \frac{1}{4_{}^{2}}} + ⋯ + \sqrt{1 + \frac{1}{202 2_{}^{2}} + \frac{1}{202 3_{}^{2}}}$

查看试题解析
24. 问题：如图，在平行四边形ABCD中，AB＝10，AD＝6，∠DAB，∠ABC的平分线AE、BF分别与直线CD交于点E、F，请直接写出EF的长.

(1)、把“问题”中的条件“AB＝10，AD＝6”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求 $\frac{A D}{A B}$ 的值.

(2)、探究：把“问题”中的条件“AB＝10”去掉，其余条件不变.

①当点E与点F重合时，AB的长为.

②当点E与点C重合时，EF的长为.

查看试题解析

	1号	2号	3号	4号	5号	总数
甲班	89	100	96	118	97	500
乙班	100	95	110	91	104	500