浙江省杭州市富阳区余杭区2023年中考一模数学试题

试卷更新日期：2023-04-23 类型：中考模拟

进入出卷网下载

一、选择题（本大题有10个小题，每小题3分，共30分．）

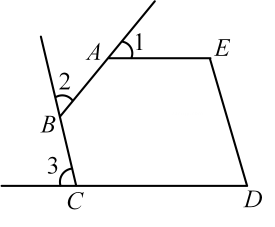
1. |-2|等于（）

A、-2 B、2 C、 $\frac{1}{2}$ D、- $\frac{1}{2}$

查看试题解析
2. 2022年杭州市的GDP达到18800亿元，用科学记数法表示“18800亿”正确的是（）

A、0.188×10¹³ B、1.88×10¹² C、1.88×10¹³ D、1.818×10¹⁴

查看试题解析
3. 下列计算正确的是（）

A、 $(- 1)^{2023} = - 2023$ B、 $- 3^{2} = 9$ C、 $\sqrt{4} = \pm 2$ D、 ${(a^{3})}^{2} = a^{6}$

查看试题解析
4. 如图，五边形ABCDE中，AE//CD，∠1、∠2、∠3分别是∠EAB、∠ABC、∠BCD的外角，则∠1+∠2+∠3=（）

A、90° B、150° C、180° D、210°

查看试题解析
5. 在△ABC中，∠C＝90°，sinB＝ $\frac{4}{5}$ ，则tanA＝（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 如图，小宁连续两周居家记录的体温情况折线统计图，下列从图中获得的信息正确的是（）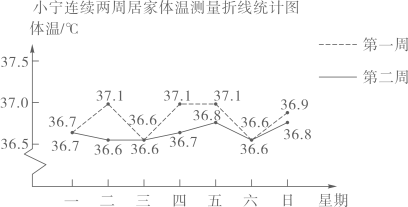

A、这两周体温的众数为36.6℃ B、第一周体温的中位数为37.1℃ C、第二周平均体温高于第一周平均体温 D、第一周的体温比第二周的体温更加平稳

查看试题解析
7. 反比例函数 $y = \frac{12}{x}$ 图象上有三个点 $(x_{1} ， y_{1}) ， (x_{2} ， y_{2}) ， (x_{3} ， y_{3})$ ，其中 $x_{1} < x_{2} < 0 < x_{3}$ ，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB＝90°，分别以它的三边为边向外作正方形ADEB，正方形BKGC，正方形ACHF，过点C作CL⊥DE于点L，交AB于点M.若四边形LEBM和四边形ACHF的面积分别是25，135，则AB的长为（）

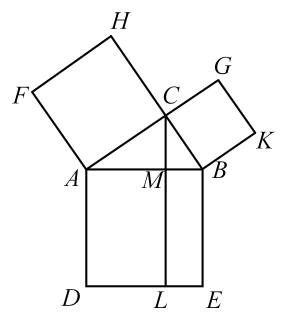A、160 B、110 C、 $4 \sqrt{10}$ D、 $\sqrt{110}$

查看试题解析
9. 十字路口红绿灯时长设置是根据路口的实际车流状况来分配的.据统计，某十字路口每天的车流量中，东西走向直行与左转车辆分别约占总流量 $\frac{1}{4}$ ， $\frac{1}{5}$ ；南北走向直行与左转车辆分别约占总流量 $\frac{1}{10}$ ， $\frac{1}{5}$ 。因右转车辆不受红绿灯限制，所以在设置红绿灯时，按东西走向直行、左转，南北走向直行、左转的次序依次亮起绿灯作为一个周期时间(当某方向绿灯亮起时，其他3个方向全为红灯)，若一个周期时间为2分钟，则应设置南北走向直行绿灯时长较为合理的是（）

A、12秒 B、16秒 C、18秒 D、24秒

查看试题解析
10. 有一列数，记为 $a_{1} ， a_{2} ， ⋯ ， a_{n}$ ，记其前 $n$ 项和为 $S_{n} = a_{1} + a_{2} + ⋯ + a_{n}$ ，定义 $T_{n} = \frac{S_{1} + S_{2} + ⋯ + S_{n}}{n}$ 为这列数的“亚运和”，现有 99 个数 $a_{1} ， a_{2} ， ⋯ ， a_{99}$ ，其“亚运和”为 1000，则 $1 ， a_{1} ， a_{2} ， ⋯ ， a_{99}$ 这 100 个数的“亚运和”为（）

A、791 B、891 C、991 D、1001

查看试题解析

二、填空题（本题有6个小题，每小题4分，共24分）

11. 因式分解：x²+x=

查看试题解析
12. 已知m+n=1，m-n=3，则m²+n²=.

查看试题解析
13. 一个圆锥的底面半径为2cm，母线长为6cm，则此圆锥的侧面展开图扇形的圆心角等于度.

查看试题解析
14. 如图，小明行李箱密码锁的密码是由“3，6，9”这三个数组合而成的三位数（不同数位上的数字不同)，现随机输入这三个数，一次就能打开行李箱的概率为.

查看试题解析
15. 已知二次函数y=x²+bx+c的图象与x轴恰有一个交点，且过点A（1，n）和点B（2023，n），则 $\frac{n}{2022}$ =.

查看试题解析
16. 如图，D是△ABC的边BC上一点，△ADC沿AD翻折，C点落在点E处，AE与BC相交于F点，若EF=4，CF=14，AF=AD，则FD=.

查看试题解析

三、解答题（本题有7个小题，共66分）

17. 解方程： $\frac{3 x - 2}{3} - 1 = \frac{5 - 4 x}{6}$

查看试题解析
18. 近年来，随着人们健康睡眠的意识不断提高，社会各界对于初中生的睡眠时间是否充足越发关注．近日我市某学校从全校1200人中随机抽取了部分同学，调查他们平均每日睡眠时间，将得到的数据整理后绘制了如图所示的扇形统计图和频数分布直方图：

(1)、本次接受调查人数为；图中a=；b=；c=.

(2)、教育部《关于进一步加强中小学生睡眠管理工作的通知》文件指出，初中生睡眠时间应达到9小时，试估算该校学生睡眠时间达标人数．

查看试题解析
19. 如图，在△ABC中，∠A=30°，∠B=45°，AC= $2 \sqrt{2}$ .

(1)、求AB的长；

(2)、用尺规作三角形ABC的外接圆（不写作法，保留作图痕迹），并求此外接圆的半径.

查看试题解析
20. 已知y与x+m（m为常数）成正比例，且当x=3时y=5，当x=1时y=1.

(1)、求y关于x的函数表达式；

(2)、若点P（a，b）在（1）中函数的图象上，求4a²-b²-2b-3的值.

查看试题解析
21. 如图，正方形ABCD，E，F分别在边BC，AB上，BE=BF，AE，CF交于点P.

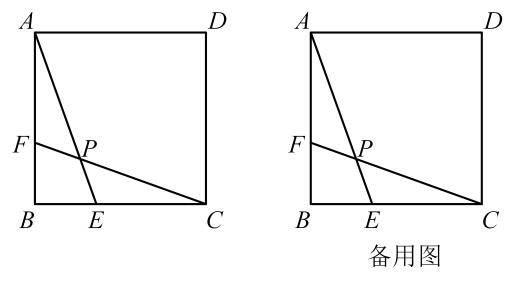(1)、求证：△ABE≌△CBF；

(2)、若AB=6，BE=2，求PC的长.

查看试题解析
22. 已知二次函数y=mx²-4mx-4（m≠0且m为常数）与y轴交于点A，其对称轴与x轴交于点B．

(1)、求点A，B的坐标；

(2)、若m＜-2，判断二次函数图象的顶点位于哪个象限，并说明理由；

(3)、若方程mx²-4mx-4=0（m≠0）有两个不相等的实数根，且两根都在1，3之间（包括1，3），结合函数的图象，求m的取值范围．

查看试题解析
23. 如图，点A，B，C分别是⊙O上的三等分点，连接AB，BC，CA.点D，E分别是AC，BC上的点，且BE=CD.过点D作EO的垂线，垂足为H，与⊙O分别交于N、M，与边AB交于F点.

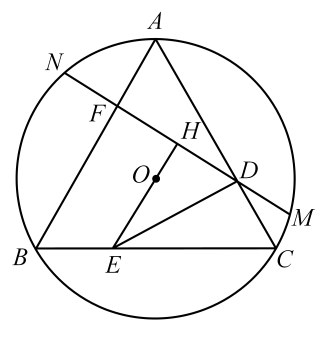(1)、求证：△ABC是等边三角形；

(2)、探索FN与MD的数量关系，并加以证明；

(3)、点E从点B沿BC方向运动到点C，点H也随之运动，若ʘO的半径为2，则点H运动的路径长是多少？

查看试题解析