浙江省温州市瓯海区2022-2023学年八年级下学期期中数学试题

试卷更新日期：2023-04-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下面的图形是用数学家的名字命名的，其中既是中心对称图形又是轴对称图形的是（）

A、科克曲线 B、费马螺线 C、笛卡尔心形线 D、斐波那契螺旋线

查看试题解析
2. 要使 $\sqrt{8 + 2 x}$ 有意义，则（）

A、 $x < - 4$ B、 $x \leq - 4$ C、 $x \geq - 4$ D、 $x > - 4$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$

查看试题解析
4. 已知数据 x₁ ， x₂ ， …xn的平均数是2，则3x₁－2，3x₂－2，…，3xn－2的平均数为（）

A、2 B、0 C、6 D、4

查看试题解析
5. 用配方法解一元二次方程 x²-10x＋11＝0，此方程可化为（）

A、（x－5）²＝14 B、（x＋5）²＝14 C、（x－5）² ＝36 D、（x＋5）² ＝36

查看试题解析
6. 正多边形的一个内角为135°，则该多边形的边数为（）

A、9 B、8 C、7 D、4

查看试题解析
7. 如图，平行四边形ABCD中，P是形内任意一点，△ABP，△BCP，△CDP，△ADP的面积分别为S₁ ， S₂ ， S₃ ， S₄ ，则一定成立的是（）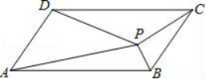

A、S₁+S₂＞S₃+S₄ B、S₁+S₂=S₃+S₄ C、S₁+S₂＜S₃+S₄ D、S₁+S₃=S₂+S₄

查看试题解析
8. 已知关于x的一元二次方程 $k x^{2} - 4 \sqrt{2} x + 2 = 0$ 有两个不相等的实数根，则k的取值范围是（）

A、 $k < 4$ B、 $k < 4$ 且 $k \neq 0$ C、 $k \geq - 4$ 且 $k \neq 0$ D、 $k \leq - 4$ 且 $k \neq 0$

查看试题解析
9. 某制药厂生产的某种针剂，每支成本3元，由于连续两次降低成本，现在的成本是2.43元，则平均每次降低成本的百分率是（）

A、 $10 ％$ B、 $20 ％$ C、 $7 ％$ D、 $8 ％$

查看试题解析
10. 如图，在 $▱ A B C D$ 中，连接 $B D$ ，且 $B D = C D$ ，过点A作 $A M ⊥ B D$ 于点M，过点D作 $D N ⊥ A B$ 于点N，且 $D N = 6$ ，在 $D B$ 的延长线上取一点P，满足 $∠ A B D = ∠ M A P + ∠ P A B$ ，则 $A P =$ （）

A、8 B、10 C、 $6 \sqrt{2}$ D、 $6 \sqrt{3}$

查看试题解析

二、填空题

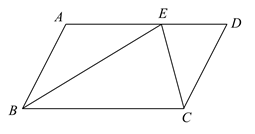
11. 一个长方形的长 $a = \sqrt{2} c m$ ，宽 $b = \sqrt{6} c m$ ，则这个长方形的面积是 $c m^{2}$ .

查看试题解析
12. 当 $x = - 1$ 时，代数式 $\sqrt{9 - 7 x}$ 的值为.

查看试题解析
13. 某班级共有50名学生，其中30名男生的平均身高是 $1.70 m$ ， 20名女生的平均身高是 $1.58 m$ ，那么这个班级学生的平均身高是m.

查看试题解析
14. 若一组数据2，3，x，5，7的众数为7，则这组数据的中位数为。

查看试题解析
15. 关于x的方程ax²+bx+2＝0的两根为x₁＝-2，x₂＝3.则方程a（x-2）²+b（x-2）+2＝0的两根分别为.

查看试题解析
16. 设m是方程 $x^{2} - x - 2023 = 0$ 的一个根，则 $m^{2} - m + 1$ 的值为.

查看试题解析
17. 如图，在 $▱ A B C D$ 中，点E在 $A D$ 上，且 $E C$ 平分 $∠ B E D$ ，若 $∠ E B C = 30 °$ ， $B E = 10$ ，则 $▱ A B C D$ 的面积为.

查看试题解析
18. 已知 $\sqrt{4 - 2 x}$ ＋ $\sqrt{2 x - 4}$ ＝y－2，则代数式 $\sqrt{\frac{x}{y} + \frac{y}{x} + 2}$ － $\sqrt{\frac{x}{y} + \frac{y}{x} - 2}$ ＝．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{18} - \sqrt{8} + (\sqrt{3} + 1) (\sqrt{3} - 1)$

(2)、 $\frac{\sqrt{2}}{\sqrt{6} - \sqrt{2}}$

查看试题解析
20. 解方程：

(1)、 $x^{2} - 4 x - 5 = 0$

(2)、 $x (2 x - 3) = 4 x - 6$

查看试题解析

21. 我校举行“文学经典我来诵”为主题的红色经典朗诵比赛，七，八年根据初赛成绩，各选出5个班级组成七年级代表队和八年级代表队参加学校决赛，两个队各选出的5个班级的决赛成绩如图所示.

	平均数（分）	中位数（分）	众数（分）
七年级队	____	85	____
八年级队	85	____	100

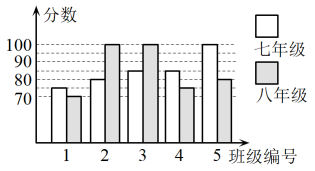(1)、根据图示填写表；

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定.

查看试题解析

22. 如图所示， $△ A B C$ ≌ $△ E A D$ ，点E在 $B C$ 上.

(1)、求证：四边形 $A B C D$ 是平行四边形；

(2)、若 $∠ B ： ∠ C A D = 5 ： 4$ ， $A E ⊥ E D$ ，求 $∠ E D C$ 的度数.

查看试题解析
23. 方方同学在寒假社会调查实践活动中，对某罐头加工厂进行采访，获得了该厂去年的部分生产信息如下：
①该厂一月份罐头加工量为a吨；

②该厂三月份的加工量比一月份增长了44％；

③该厂第一季度共加工罐头182吨；

④该厂二月、三月加工量每月按相同的百分率增长；

⑤该厂从四月份开始设备整修更新，加工量每月按相同的百分率开始下降；

⑥六月份设备整修更新完毕，此月加工量为一月份的2.1倍，与五月份相比增长了46.68吨．

利用以上信息求：

(1)、该厂第一季度加工量的月平均增长率；

(2)、该厂一月份的加工量a的值；

(3)、该厂第二季度的总加工量．

查看试题解析
24. 点P是平行四边形 $A B C D$ 的对角线 $A C$ 所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线 $B P$ 作垂线，垂足分别为点E、F．点O为 $A C$ 的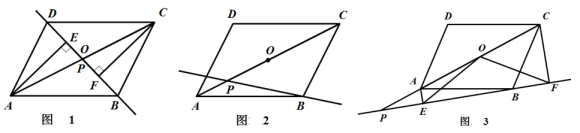中点．

(1)、如图1，当点P与点O重合时，线段OE和OF的关系是；

(2)、当点P运动到如图2所示的位置时，请在图中补全图形并通过证明判断（1）中的结论是否仍然成立？

(3)、如图3，点P在线段 $O A$ 的延长线上运动，当 $∠ O E F = 30 °$ 时，试探究线段 $C F$ 、 $A E$ 、 $O E$ 之间的关系．

查看试题解析