江苏省泰州市靖江市2022-2023学年九年级下学期期中数学试题

试卷更新日期：2023-04-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个实数中，相反数最小的数是（）

A、 $- 1$ B、 $0$ C、 $\sqrt{5}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下列说法正确的是（）

A、“清明时节雨纷纷”是必然事件 B、为了解某灯管的使用寿命，可以采用普查的方式进行 C、一组数据 $3 ， 5 ， 4 ， 5 ， 6 ， 7$ 的众数、中位数和平均数都是 $5$ D、两组身高数据的方差分别是 ${S_{甲}}^{2} = 0.01 ， {S_{乙}}^{2} = 0.02$ ，那么乙组的身高比较整齐

查看试题解析
3. 如图， $A B$ 是⊙O的直径，点C、D在⊙O上， $∠ B D C = 20 °$ ，则 $∠ A O C$ 的大小为（）

A、 $40 °$ B、 $140 °$ C、 $160 °$ D、 $170 °$

查看试题解析
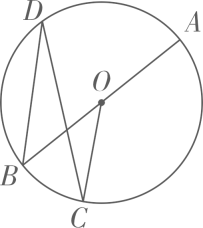4. 关于x的一元二次方程 $x^{2} + k x + 1 = 3 x + k$ 根的情况，下列说法正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
5. 如图，点 $A ， B ， C$ 在正方形网格的格点上，则 $s i n ∠ B A C =$ （）

A、 $\frac{\sqrt{13}}{13}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{\sqrt{26}}{13}$ D、 $\frac{\sqrt{26}}{26}$

查看试题解析
6. 已知点 $A (2 a - 1 ， y_{1})$ ， $B (a^{2} + 1 ， y_{2})$ 在一次函数 $y = (m^{2} + 1) x + 2 n$ （m，n为常数）的图像上，则 $y_{1}$ ， $y_{2}$ 的大小关系为（）.

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、无法判断

查看试题解析

二、填空题

7. 计算： $a^{2} \cdot a^{3} =$ .

查看试题解析
8. 已知 $R t △ A B C$ 中， $∠ C = 90 °$ ， $t a n A = \sqrt{3}$ ，则 $∠ A$ 的度数为.

查看试题解析
9. 某种芯片每个探针单元的面积为0.00000164cm² ， 0.00000164用科学记数法表示为.

查看试题解析
10. 在平面直角坐标系 $x O y$ 中，直线 $y = - 2 x$ 与双曲线 $y = \frac{m}{x}$ 交于 $A ， B$ 两点，若点 $A ， B$ 的纵坐标分别为 $y_{1} ， y_{2}$ ，则 $- 3 y_{1} - 3 y_{2}$ 的值为.

查看试题解析
11. 设a、b是方程 $x^{2} + 2 x - 2022 = 0$ 的两个不等的根，则 $a^{2} + 4 a + 2 b$ 的值.

查看试题解析
12. 如图，在 $Δ A B C$ 中， $D C$ 平分 $∠ A C B$ ， $B D ⊥ C D$ 于点D， $∠ A B D = ∠ A$ ，若 $B D = 1$ ， $A C = 7$ ，则 $c o s ∠ C B D$ 的值为.

查看试题解析
13. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ ，垂足为点M，连接 $O C ， D B$ ，如果 $O C ∥ D B$ ， $O C = 2$ ，那么图中阴影部分的面积是.

查看试题解析
14. 若点 $P (m ， n)$ 在二次函数 $y = x^{2} + 2 x + 2$ 的图像上，以P为圆心， $2$ 为半径的圆与y轴相交，则n的取值范围是.

查看试题解析
15. 等腰三角形的底边长为 $12$ ，腰长为 $10$ ，该等腰三角形内心和外心的距离为.

查看试题解析
16. 平面直角坐标系中，O为坐标原点，直线 $y = - x + 4$ 与x轴、y轴分别交于 $A ， B$ 两点，点C，点D坐标分别为 $(0 ， m) ， (4 - m ， 0) (0 < m < 4)$ ，则 $A C + B D$ 的最小值为.

查看试题解析

三、解答题

17.

(1)、计算： $| - 1 | + {(\frac{\sqrt{2}}{2})}^{- 2} - {(3 + \sqrt{5})}^{0} - \sqrt{8}$ .

(2)、解方程组 ${\begin{array}{l} 2 x - y = 4 ， \\ x + y = 2 . \end{array}$

查看试题解析
18. 化简求值： $(\frac{3}{x - 1} - x - 1) \div \frac{x - 2}{x - 1}$ ，其中x是不等式组 ${\begin{array}{l} x - 3 (x - 2) \geq 2 \\ 4 x - 2 < 5 x - 1 \end{array}$ 的一个整数解.

查看试题解析
19. 如图所示，甲、乙两个带指针的转盘分别被分成三个面积相等的扇形（两个转盘除表面数字不同外，其它完全相同），转盘甲上的数字分别是 $- 6 ， - 1 ， 8$ ，转盘乙上的数字分别是 $- 4 ， 5 ， 7$ （规定：指针恰好停留在分界线上，则重新转一次）.

(1)、单独转动转盘甲，转盘甲指针指向正数的概率是.

(2)、若同时转动两个转盘，转盘甲指针所指的数字记为a，转盘乙指针所指的数字记为b，请用列表法或树状图法求满足 $a b < 0$ 的概率.

查看试题解析

20. 某农业科技部门为了解甲、乙两种新品西瓜的品质（大小、甜度等），进行了抽样调查.在相同条件下，随机抽取了两种西瓜各7份样品，对西瓜的品质进行评分（百分制），并对数据进行收集、整理，下面给出两种西瓜得分的统计图表.

甲、乙两种西瓜得分表

序号	1	2	3	4	5	6	7
甲种西瓜（分）	75	85	86	88	90	96	96
乙种西瓜（分）	80	83	87	90	90	92	94

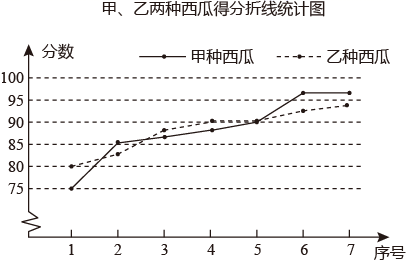
甲、乙两种西瓜得分统计表

	平均数	中位数	众数
甲种西瓜	88	a	96
乙种西瓜	88	90	b

(1)、

a =

，

b =

；

(2)、从方差的角度看，种西瓜的得分较稳定（填“甲”或“乙”）；

(3)、小明认为甲种西瓜的品质较好些，小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.

查看试题解析

21. 某市为了构建城市立体道路网络，决定修建一条快速道路，为了使工程提前半年完成，需将工作效率提高 $40 ％$ ，原计划完成这项工程需要几个月？

查看试题解析
22. 某兴趣小组研制的智能操作机器人，如图1，水平操作台为l，高 $A B$ 为 $50 c m$ ，连杆 $B C$ 长度为 $70 c m$ ，手臂 $C D$ 的长度为 $60 c m$ ， $B ， C$ 是转动点，且 $A B 、 B C$ 与 $C D$ 始终在同一平面内.

(1)、转动连杆 $B C$ ，手臂 $C D$ ，使 $∠ A B C = 143 °$ ， $C D ∥ l$ ，如图2，求手臂端点D离操作台l的高度 $D E$ 的长（精确到 $1 c m$ ，参考数据： $s i n 53 ° \approx 0.8 ， c o s 53 ° \approx 0.6$ ）.

(2)、物品在操作台l上，距离底座A端 $122 c m$ 的点M处，转动连杆 $B C$ ，手臂端点D能否碰到点M？请说明理由.

查看试题解析
23. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点O为 $A C$ 上一点，以点O为圆心， $O C$ 为半径的 $⊙ O$ 与 $A B$ 相切于点D， $A E ⊥ B O$ 交 $B O$ 延长线于点E.

(1)、求证： $∠ E O A = ∠ E A B$ .

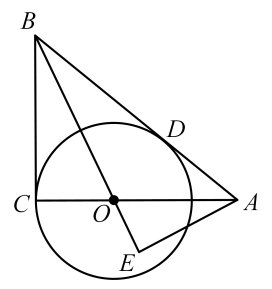(2)、若 $O E = \sqrt{5} ， A E = 2 \sqrt{5}$ ，求 $O C$ 的长.

查看试题解析
24. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b$ 的图象经过点 $A (0 ， - 4)$ ， $B (2 ， 0)$ ，交反比例函数 $y_{2} = \frac{m}{x} (x > 0)$ 的图象于点 $C (3 ， a)$ ，点P在反比例函数的图象上，横坐标为 $n (0 < n < 3)$ ， $P Q ∥ y$ 轴交直线 $A B$ 于点Q，D是y轴上任意一点，连接 $P D$ 、 $Q D$ .

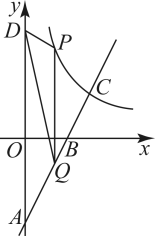(1)、求一次函数和反比例函数的表达式.

(2)、求当 $△ P D Q$ 面积等于2时n的值.

查看试题解析
25. 如图，在矩形 $A B C D$ 中， $A B = 3 ， A D = 3 \sqrt{3}$ .点 $E 、 F$ 分别在 $A D 、 B C$ 上，四边形 $B E D F$ 为菱形.

(1)、利用尺规作图在图 $1$ 中作出菱形 $B E D F$ （不写作法，保留作图痕迹）.

(2)、如图 $2$ ，动点M从点E出发沿射线 $E D$ 方向运动，同时，动点N从点F出发沿射线 $D F$ 方向运动，且 $M 、 N$ 两点运动速度相同， $B M 、 E N$ 相交于点P.
①求 $∠ E P M$ 的度数.

②连接 $C P$ ，线段 $C P$ 长度的最小值为 ▲ .

查看试题解析
26. 定义：两个二次项系数之和为 $1$ ，对称轴相同，且图像与y轴交点也相同的二次函数互为友好同轴二次函数.例如： $y = 2 x^{2} + 4 x - 5$ 的友好同轴二次函数为 $y = - x^{2} - 2 x - 5$ .

(1)、函数 $y = \frac{1}{4} x^{2} - 2 x + 3$ 的友好同轴二次函数为.

(2)、当 $- 1 \leq x \leq 4$ 时，函数 $y = (1 - a) x^{2} - 2 (1 - a) x + 3$ $(a \neq 0 且 a \neq 1)$ 的友好同轴二次函数有最大值为 $5$ ，求 $a$ 的值.

(3)、已知点 $(m ， p) ， (m ， q)$ 分别在二次函数 $y_{1} = a x^{2} + 4 a x + c (a > \frac{1}{2} 且 a \neq 1 ）$ 及其友好同轴二次函数 $y_{2}$ 的图像上，比较 $p ， q$ 的大小，并说明理由.

查看试题解析