湖南省张家界市永定区2022-2023学年八年级下学期期中质量监测数学试题
试卷更新日期:2023-04-23 类型:期中考试
一、单选题
-
1. 在中, , 若 , 则等于( )A、 B、 C、 D、2. 如图,在中, , 平分 , , , 那么点到直线的距离是( )
 A、 B、 C、 D、3. 一个多边形每个内角都是150°,这个多边形是( )A、九边形 B、十边形 C、十二边形 D、十八形4. 如图,在中,过点B作交延长线于点E,若 , 则的度数为( )
A、 B、 C、 D、3. 一个多边形每个内角都是150°,这个多边形是( )A、九边形 B、十边形 C、十二边形 D、十八形4. 如图,在中,过点B作交延长线于点E,若 , 则的度数为( ) A、 B、 C、 D、5. 下列命题中,假命题是( )A、平行四边形的对角线相等 B、正方形的对角线互相垂直平分 C、对角线互相垂直的平行四边形是菱形 D、有一个角为的平行四边形是矩形6. 下列各组数中,是勾股数的是( )A、0.3,0.4,0.5 B、1,2,3 C、5,12,13 D、3,4,7. 如图所示的一段楼梯,高BC是3米,斜边AB长是5米,现打算在楼梯上铺地毯,至少需要地毯的长度为( )
A、 B、 C、 D、5. 下列命题中,假命题是( )A、平行四边形的对角线相等 B、正方形的对角线互相垂直平分 C、对角线互相垂直的平行四边形是菱形 D、有一个角为的平行四边形是矩形6. 下列各组数中,是勾股数的是( )A、0.3,0.4,0.5 B、1,2,3 C、5,12,13 D、3,4,7. 如图所示的一段楼梯,高BC是3米,斜边AB长是5米,现打算在楼梯上铺地毯,至少需要地毯的长度为( ) A、5米 B、6米 C、7米 D、8米8. 如图,正方形ABCD的边长为4,点M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为( )
A、5米 B、6米 C、7米 D、8米8. 如图,正方形ABCD的边长为4,点M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为( ) A、4 B、 C、 D、5
A、4 B、 C、 D、5二、填空题
-
9. 如图, , 请你再添加一个条件,使 , 你添加的条件是.
 10. 如图,菱形ABCD的对角线AC=3cm,BD=4cm,则菱形ABCD的面积是.
10. 如图,菱形ABCD的对角线AC=3cm,BD=4cm,则菱形ABCD的面积是. 11. 如图,矩形ABCD中,AC、BD相交于点O且AC=12,如果∠AOD=60°,则DC=.
11. 如图,矩形ABCD中,AC、BD相交于点O且AC=12,如果∠AOD=60°,则DC=. 12. 如图,在△ABC中,AB=AC , 以点B为圆心,小于AB长为半径作弧,分别交AB、BC于点E、F , 再分别以点E、F为圆心,以大于 长为半径作弧,两弧相交于点G , 连结BG并延长交AC于点D , 若∠A=80°,则∠ADB=度.
12. 如图,在△ABC中,AB=AC , 以点B为圆心,小于AB长为半径作弧,分别交AB、BC于点E、F , 再分别以点E、F为圆心,以大于 长为半径作弧,两弧相交于点G , 连结BG并延长交AC于点D , 若∠A=80°,则∠ADB=度.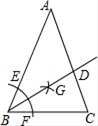 13. 已知等腰的底边 , D是腰上一点,且 , , 则的长为.
13. 已知等腰的底边 , D是腰上一点,且 , , 则的长为. 14. 如图,和都是等边三角形,A、B、D三点共线.下列结论:①;②;③平分;④ , ⑤是等边三角形.其中正确的有(只填序号).
14. 如图,和都是等边三角形,A、B、D三点共线.下列结论:①;②;③平分;④ , ⑤是等边三角形.其中正确的有(只填序号).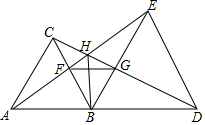
三、解答题
-
15. 已知一个正多边形的内角和比外角和多 , 求这个正多边形的边数和每个外角的度数.16. 如图,D为边上的一点, , , , , 求的长.
 17. 如图,在中, , , 于E,点F在边上.
17. 如图,在中, , , 于E,点F在边上. (1)、求证:;(2)、若 , , 求出的面积以及的长.18. 已知:四边形是正方形,E、F分别是和的延长线上的点,且 , 连接、、.
(1)、求证:;(2)、若 , , 求出的面积以及的长.18. 已知:四边形是正方形,E、F分别是和的延长线上的点,且 , 连接、、. (1)、求证:;(2)、证明:.19. 如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF.
(1)、求证:;(2)、证明:.19. 如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF. (1)、求证:△ABE≌△CDF;(2)、当AC⊥EF时,四边形AECF是菱形吗?请说明理由.20. 如图,有两只猴子在一棵树CD高6m的点B处,他们都要到A处的池塘去喝水,其中一只猴子沿树爬下去到离树12m处的池塘A处,另一只猴子爬到树顶D后直线越向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米?
(1)、求证:△ABE≌△CDF;(2)、当AC⊥EF时,四边形AECF是菱形吗?请说明理由.20. 如图,有两只猴子在一棵树CD高6m的点B处,他们都要到A处的池塘去喝水,其中一只猴子沿树爬下去到离树12m处的池塘A处,另一只猴子爬到树顶D后直线越向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米? 21. 已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且 , 联结CM、DN.
21. 已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且 , 联结CM、DN.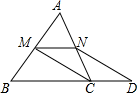 (1)、求证:四边形MCDN是平行四边形;(2)、若三角形AMN的面积等于5,求梯形MBDN的面积.22. 如图,海中有一小岛P,它的周围12海里内有暗礁,渔船跟踪鱼群由西向东航行,在M处测得小岛P在北偏东60°方向上,航行16海里到N处,这时测得小岛P在北偏东30°方向上.
(1)、求证:四边形MCDN是平行四边形;(2)、若三角形AMN的面积等于5,求梯形MBDN的面积.22. 如图,海中有一小岛P,它的周围12海里内有暗礁,渔船跟踪鱼群由西向东航行,在M处测得小岛P在北偏东60°方向上,航行16海里到N处,这时测得小岛P在北偏东30°方向上.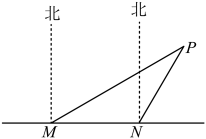 (1)、求M点与小岛P的距离;(2)、如果渔船不改变航线继续向东航行,是否有触礁危险,并说明理由.23. 如图,在梯形中, , , , , , 动点P从A点开始沿边向D以秒的速度运动,动点Q从C点开始沿边向B以秒的速度运动,P、Q分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t秒.问:
(1)、求M点与小岛P的距离;(2)、如果渔船不改变航线继续向东航行,是否有触礁危险,并说明理由.23. 如图,在梯形中, , , , , , 动点P从A点开始沿边向D以秒的速度运动,动点Q从C点开始沿边向B以秒的速度运动,P、Q分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t秒.问: (1)、求t为何值时,四边形是平行四边形?(2)、四边形可能是矩形吗?如果可能,求出t的值;如果不可能,说明理由;(3)、四边形可能是菱形吗?如果可能,求出t的值;如果不可能,说明理由.
(1)、求t为何值时,四边形是平行四边形?(2)、四边形可能是矩形吗?如果可能,求出t的值;如果不可能,说明理由;(3)、四边形可能是菱形吗?如果可能,求出t的值;如果不可能,说明理由.