福建省三明市大田县2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-04-23 类型:期中考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 国产手机芯片麒麟是全球首个纳米制程芯片,已知纳米米,将纳米用科学记数法表示为( )A、米 B、米 C、米 D、米3. 将一副三角板按不同位置摆放,下图中与互余的是( )A、
 B、
B、 C、
C、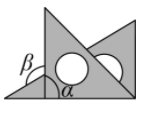 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,小华同学的家在点处,他想尽快到达公路边去接从外地回来的外婆,他选择路线时所用到的数学知识是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,小华同学的家在点处,他想尽快到达公路边去接从外地回来的外婆,他选择路线时所用到的数学知识是( ) A、两点确定一条直线 B、两点之间直线最短 C、两点之间线段最短 D、垂线段最短6. 父亲告诉小明,温度与海拔高度有关系,并给小明出示了下面的表格:
A、两点确定一条直线 B、两点之间直线最短 C、两点之间线段最短 D、垂线段最短6. 父亲告诉小明,温度与海拔高度有关系,并给小明出示了下面的表格:海拔高度/km
0
1
2
3
4
5
…
温度/℃
20
14
8
2
-4
-10
…
下列有关表格的分析中,不正确的是( )
A、表格中的两个变量是海拔高度和温度 B、自变量是海拔高度 C、海拔高度越高,温度就越低 D、海拔高度每增加1km,温度升高6℃7. 如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为 , 宽为的大长方形,则需要C类卡片( ) A、5张 B、6张 C、7张 D、8张8. 已知a∥b , 将等腰直角三角形ABC按如图所示的方式放置,其中锐角顶点B , 直角顶点C分别落在直线a , b上,若∠1 15°,则∠2的度数是( )
A、5张 B、6张 C、7张 D、8张8. 已知a∥b , 将等腰直角三角形ABC按如图所示的方式放置,其中锐角顶点B , 直角顶点C分别落在直线a , b上,若∠1 15°,则∠2的度数是( )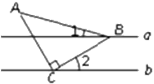 A、15° B、22.5° C、30° D、45°9. 如图在边长为a的正方形中挖掉一个边长为b的小正方形().把余下的部分前拼成一个矩形,通过计算阴影部分的面积,验证了一个等式,则这个等式是( )
A、15° B、22.5° C、30° D、45°9. 如图在边长为a的正方形中挖掉一个边长为b的小正方形().把余下的部分前拼成一个矩形,通过计算阴影部分的面积,验证了一个等式,则这个等式是( ) A、 B、 C、 D、10. 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段的长为y.表示y与x之间关系的图象大致如图所示,则该封闭图形可能是( )
A、 B、 C、 D、10. 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段的长为y.表示y与x之间关系的图象大致如图所示,则该封闭图形可能是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 计算:3x(x-2)=.12. 如图是对顶角量角器,它所测量的角是度.
 13. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y= x+32,如果某一温度的摄氏度数是25℃,那么它的华氏度数是℉.14. 如果多项式()是一个完全平方式,则的值是.15. 如图, , ,则 的度数是 .
13. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y= x+32,如果某一温度的摄氏度数是25℃,那么它的华氏度数是℉.14. 如果多项式()是一个完全平方式,则的值是.15. 如图, , ,则 的度数是 . 16. 已知 , , , 现给出a,b,c之间的四个关系式:①;②;③;④.其中正确的关系式是.(填序号).
16. 已知 , , , 现给出a,b,c之间的四个关系式:①;②;③;④.其中正确的关系式是.(填序号).三、解答题
-
17.(1)、计算:;(2)、化简:.18.(1)、;(2)、19. 如图 , D为的延长线上一点.
 (1)、用尺规作图的方法在上方作 , 使;(2)、在(1)的条件下,若 , 恰好平分 , 求的度数.20. 先化简,再求值: , 其中 , .21. 为了加强公民的节水意识.某市规定用水收费标准如下.每户每月用水量不超过12时.按照每立方米3.5元收费:超过时,超出部分每立方米按4.5元收费.设每月用水量为 , 应缴水费为y元.(1)、当月用水量不超过时,y(元)与之间的关系式为;当月用水量超过时,y(元)与之间的关系式为.(2)、若某户某月缴纳水费55.5元,则该户这个月的用水量为多少?22. 如图, , .
(1)、用尺规作图的方法在上方作 , 使;(2)、在(1)的条件下,若 , 恰好平分 , 求的度数.20. 先化简,再求值: , 其中 , .21. 为了加强公民的节水意识.某市规定用水收费标准如下.每户每月用水量不超过12时.按照每立方米3.5元收费:超过时,超出部分每立方米按4.5元收费.设每月用水量为 , 应缴水费为y元.(1)、当月用水量不超过时,y(元)与之间的关系式为;当月用水量超过时,y(元)与之间的关系式为.(2)、若某户某月缴纳水费55.5元,则该户这个月的用水量为多少?22. 如图, , . (1)、求证:;(2)、若 , , 求的度数.23. 如图1,平行四边形的一边向左右匀速平行移动,图2反映它的底边的长度随时间变化而变化的情况,图3反映了变化过程中平行四边形的面积随时间变化的情况.
(1)、求证:;(2)、若 , , 求的度数.23. 如图1,平行四边形的一边向左右匀速平行移动,图2反映它的底边的长度随时间变化而变化的情况,图3反映了变化过程中平行四边形的面积随时间变化的情况. (1)、平行四边形中,边上的高为;(2)、当时,写出面积与时间之间的关系式;(3)、当时,求面积S的值.24. 完全平方公式:适当的变形,可以解决很多的数学问题.
(1)、平行四边形中,边上的高为;(2)、当时,写出面积与时间之间的关系式;(3)、当时,求面积S的值.24. 完全平方公式:适当的变形,可以解决很多的数学问题.例如:若 , , 求的值,
解:因为 , ,
所以 , ,
所以 , 得.
根据上面的解题思路与方法,解决下列问题:
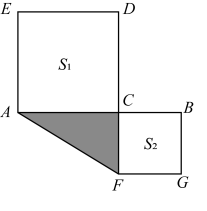 (1)、若 , , 求的值;(2)、若;(3)、如图,点C是线段上的一点,以、为边向两边作正方形,设 , 两正方形的面积和 , 求图中阴影部分面积.25. 如图1,直线与直线交于点O,().小明将一个含 , 的直角三角板如图1所示放置,使顶点P落在直线上,过点Q作直线交直线于点H(点H在Q左侧).
(1)、若 , , 求的值;(2)、若;(3)、如图,点C是线段上的一点,以、为边向两边作正方形,设 , 两正方形的面积和 , 求图中阴影部分面积.25. 如图1,直线与直线交于点O,().小明将一个含 , 的直角三角板如图1所示放置,使顶点P落在直线上,过点Q作直线交直线于点H(点H在Q左侧). (1)、若 , , 求的度数.(2)、如图2,若的角平分线交直线于点E.
(1)、若 , , 求的度数.(2)、如图2,若的角平分线交直线于点E.①当 , 时,求证:.
②小明将三角板保持并向左平移,运动过程中,探究与之间的数量关系,并说明理由.