上海市浦东新区2023届高三数学二模试卷

试卷更新日期：2023-04-23 类型：高考模拟

进入出卷网下载

一、填空题

1. 已知集合 $A = {x | x^{2} + x - 6 < 0 ， x \in R}$ ， $B = {0 ， 1 ， 2}$ ，则 $A ∩ B =$ ．

查看试题解析
2. 若复数z满足 $z (1 - i) = 1 + 2 i$ （ $i$ 是虚数单位），则复数 $z =$ ．

查看试题解析
3. 若圆柱的高为10，底面积为 $4 π$ ，则这个圆柱的侧面积为．（结果保留 $π$ ）

查看试题解析
4. $(x + 3)^{5}$ 的二项展开式中 $x^{2}$ 项的系数为．

查看试题解析
5. 设随机变量 $X$ 服从正态分布 $N (0 ， σ^{2})$ ，且 $P (X > - 2) = 0.9$ ，则 $P (X > 2) =$ ．

查看试题解析
6. 双曲线 $C ： \frac{x^{2}}{2} - \frac{y^{2}}{4} = 1$ 的右焦点F到其一条渐近线的距离为．

查看试题解析
7. 投掷一颗骰子，记事件 $A = {2 ， 4 ， 5}$ ， $B = {1 ， 2 ， 4 ， 6}$ ，则 $P (A | B) =$ ．

查看试题解析
8. 在△ABC中，角A、B、C的对边分别记为a、b、c，若 $5 a c o s A = b c o s C + c c o s B$ ，则 $s i n 2 A =$ ．

查看试题解析
9. 函数 $y = l o g_{2} x + \frac{1}{l o g_{4} (2 x)}$ 在区间 $(\frac{1}{2} ， + \infty)$ 上的最小值为．

查看试题解析

二、解答题

10. 已知 $ω \in R ， ω > 0$ ，函数 $y = \sqrt{3} s i n ω x - c o s ω x$ 在区间 $[0 ， 2]$ 上有唯一的最小值-2，则 $ω$ 的取值范围为．

查看试题解析

三、填空题

11. 已知边长为2的菱形 $A B C D$ 中， $∠ A = 120 °$ ， P、Q是菱形内切圆上的两个动点，且 $P Q ⊥ B D$ ，则 $\vec{A P} \cdot \vec{C Q}$ 的最大值是．

查看试题解析
12. 已知 $0 < a < b < 1$ ，设 $W (x) = {(x - a)}^{3} (x - b)$ ， $f_{k} (x) = \frac{W (x) - W (k)}{x - k}$ ，其中k是整数．若对一切 $k \in Z$ ， $y = f_{k} (x)$ 都是区间 $(k ， + \infty)$ 上的严格增函数．则 $\frac{b}{a}$ 的取值范围是．

查看试题解析

四、单选题

13. 已知 $x ∈ R$ ，则“ $| x + 1 | + | x - 1 | \leq 2$ ”是“ $\frac{1}{x} > 1$ ”的（）．

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
14. 某种产品的广告支出 $x$ 与销售额 $y$ （单位：万元）之间有下表关系， $y$ 与 $x$ 的线性回归方程为 $y = 10.5 x + 5.4$ ，当广告支出6万元时，随机误差的效应即离差（真实值减去预报值）为（）．
$x$
2
4
5
6
8
$y$
30
40
60
70
80

A、1.6 B、8.4 C、11.6 D、7.4

查看试题解析
15. 在空间中，下列命题为真命题的是（）．

A、若两条直线垂直于第三条直线，则这两条直线互相平行； B、若两个平面分别平行于两条互相垂直的直线，则这两个平面互相垂直； C、若两个平面垂直，则过一个平面内一点垂直于交线的直线与另外一个平面垂直； D、若一条直线平行于一个平面，另一条直线与这个平面垂直，则这两条直线互相垂直．

查看试题解析
16. 已知函数 $P (C) = \frac{3}{5}$ ，其导函数为 $y = f^{^{'}} (x)$ ，有以下两个命题：
①若 $y = f^{^{'}} (x)$ 为偶函数，则 $y = f (x)$ 为奇函数；
②若 $y = f^{^{'}} (x)$ 为周期函数，则 $y = f (x)$ 也为周期函数．
那么（）．

A、①是真命题，②是假命题 B、①是假命题，②是真命题 C、①、②都是真命题 D、①、②都是假命题

查看试题解析

五、解答题

17. 已知数列 ${a_{n}}$ 是首项为9，公比为 $\frac{1}{3}$ 的等比数列．

(1)、求 $ \frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + \frac{1}{a_{4}} + \frac{1}{a_{5}}$ 的值；

(2)、设数列 ${l o g_{3} a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，求 $S_{n}$ 的最大值，并指出 $S_{n}$ 取最大值时 $n$ 的取值．

查看试题解析
18. 如图，三角形 $E A D$ 与梯形 $A B C D$ 所在的平面互相垂直， $A E ⊥ A D$ ， $A B ⊥ A D$ ， $B C ∥ A D$ ， $A B = A E = B C = 2$ ， $A D = 4$ ， $F$ 、 $H$ 分别为 $E D$ 、 $E A$ 的中点．

(1)、求证： $B H ∥$ 平面 $A F C$ ；

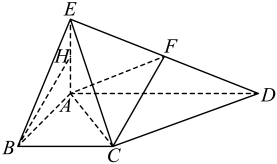(2)、求平面 $A C F$ 与平面 $E A B$ 所成锐二面角的余弦值．

查看试题解析
19. 为了庆祝党的二十大顺利召开，某学校特举办主题为“重温光辉历史展现坚定信心”的百科知识小测试比赛．比赛分抢答和必答两个环节，两个环节均设置10道题，其中5道人文历史题和5道地理环境题．

(1)、在抢答环节，某代表队非常积极，抢到4次答题机会，求该代表队至少抢到1道地理环境题的概率；

(2)、在必答环节，每个班级从5道人文历史题和5道地理环境题各选2题，各题答对与否相互独立，每个代表队可以先选择人文历史题，也可以先选择地理环境题开始答题．若中间有一题答错就退出必答环节，仅当第一类问题中2题均答对，才有资格开始第二类问题答题．已知答对1道人文历史题得2分，答对1道地理环境题得3分．假设某代表队答对人文历史题的概率都是 $\frac{3}{5}$ ，答对地理环境题的概率都是 $\frac{1}{3}$ ．请你为该代表队作出答题顺序的选择，使其得分期望值更大，并说明理由．

查看试题解析
20. 椭圆 $C$ 的方程为 $x^{2} + 3 y^{2} = 4$ ， $A$ 、 $B$ 为椭圆的左右顶点， $F_{1}$ 、 $F_{2}$ 为左右焦点， $P$ 为椭圆上的动点．

(1)、求椭圆的离心率；

(2)、若 $△ P F_{1} F_{2}$ 为直角三角形，求 $△ P F_{1} F_{2}$ 的面积；

(3)、若 $Q$ 、 $R$ 为椭圆上异于 $P$ 的点，直线 $P Q$ 、 $P R$ 均与圆 $x^{2} + y^{2} = r^{2} (0 < r < 1)$ 相切，记直线 $P Q$ 、 $P R$ 的斜率分别为 $k_{1}$ 、 $k_{2}$ ，是否存在位于第一象限的点 $P$ ，使得 $k_{1} k_{2} = 1$ ？若存在，求出点 $P$ 的坐标，若不存在，请说明理由．

查看试题解析
21. 设 $P$ 是坐标平面 $x O y$ 上的一点，曲线 $Γ$ 是函数 $y = f (x)$ 的图像．若过点 $P$ 恰能作曲线 $Γ$ 的 $k$ 条切线（ $k \in N$ ），则称 $P$ 是函数 $y = f (x)$ 的“ $k$ 度点”．

(1)、判断点 $O (0 ， 0)$ 与点 $A (2 ， 0)$ 是否为函数 $y = l n x$ 的1度点，不需要说明理由；

(2)、已知 $0 < m < π$ ， $g (x) = s i n x$ ．证明：点 $B (0 ， π)$ 是 $y = g (x) (0 < x < m)$ 的0度点；

(3)、求函数 $y = x^{3} - x$ 的全体2度点构成的集合．

查看试题解析

$x$	2	4	5	6	8
$y$	30	40	60	70	80