上海市黄浦区2023届高三数学二模试卷

试卷更新日期：2023-04-23 类型：高考模拟

进入出卷网下载

一、填空题

1. 设集合 $A = {1 ， 3 ， 5 ， 7 ， 9} ， B = {x ∣ 2 \leq x \leq 5}$ ，则 $A ∩ B =$ ．

查看试题解析
2. 函数 $y = 4 c o s 2 x + 3$ 的最小正周期为．

查看试题解析
3. 若函数 $y = x^{a}$ 的图像经过点 $(2 ， 16)$ 与 $(3 ， m)$ ，则m的值为．

查看试题解析
4. 设复数 $z_{1}$ 、 $z_{2}$ 在复平面内的对应点关于虚轴对称， $z_{1} = 2 + i$ （ $i$ 为虚数单位），则 $z_{1} \cdot z_{2} =$ .

查看试题解析
5. 以抛物线 $y^{2} = 4 x$ 的焦点为圆心，且与抛物线的准线相切的圆的方程为.

查看试题解析
6. 已知m是 $m - 2$ 与4的等差中项，且 $(m + x)^{5} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}$ ，则 $a_{3}$ 的值为．

查看试题解析
7. 已知函数 $y = f (x)$ 是定义在 $R$ 上的奇函数，且当 $x < 0$ 时， $f (x) = e^{a x}$ ．若 $f (l n 2) = - 4$ ，则实数a的值为．

查看试题解析
8. 如图，某学具可看成将一个底面半径与高都为 $10 c m$ 的圆柱挖去一个圆雉（此圆锥的顶点是圆柱的下底面圆心、底面是圆柱的上底面）所得到的几何体，则该学具的表面积为 $c m^{2}$ ．

查看试题解析
9. 若函数 $y = f (x)$ 的图像可由函数 $y = 3 s i n 2 x - \sqrt{3} c o s 2 x$ 的图像向右平移 $φ (0 < φ < π)$ 个单位所得到，且函数 $y = f (x)$ 在区间 $[0 ， \frac{π}{2}]$ 上是严格减函数，则 $φ =$ ．

查看试题解析
10. 若每经过一天某种物品的价格变为原来的1.02倍的概率为0.5，变为原来的0.98倍的概率也为0.5，则经过6天该物品的价格较原来价格增加的概率为．

查看试题解析
11. 如图．在直角梯形 $A B C D$ 中． $A D ∥ B C ， ∠ A B C = 90 ° ， A D = 2 ， B C = 1$ ，点P是腰 $A B$ 上的动点，则 $| 2 \vec{P C} + \vec{P D} |$ 的最小值为．

查看试题解析
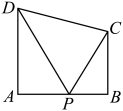12. 已知实数a，b，c满足： $a + b + c = 0$ 与 $a^{2} - b c = 3$ ，则abc的取值范围为．

查看试题解析

二、单选题

13. 若直线 $(a - 1) x + y - 1 = 0$ 与直线 $3 x - a y + 2 = 0$ 垂直，则实数a的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{2}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
14. 从装有两个红球和两个白球的口袋内任取两个球，那么互斥而不对立的事件是（）

A、恰好有一个白球与都是红球 B、至多有一个白球与都是红球 C、至多有一个白球与都是白球 D、至多有一个白球与至多一个红球

查看试题解析
15. 如图． $△ A B D$ 与 $△ B C D$ 都是等腰直角三角形．其底边分别为BD与BC，点E、F分别为线段BD、AC的中点．设二面角 $A - B D - C$ 的大小为 $α$ ，当 $α$ 在区间 $(0 ， π)$ 内变化时、下列结论正确的是（）

A、存在某一 $α$ 值．使得 $A C ⊥ B D$ B、存在某一 $α$ 值．使得 $E F ⊥ B D$ C、存在某一 $α$ 值．使得 $E F ⊥ C D$ D、存在某一 $α$ 值，使得 $A B ⊥ C D$

查看试题解析
16. 设数列 ${a_{n}}$ 的前n项的和为 $S_{n}$ ，若对任意的 $n \in N^{*}$ ，都有 $S_{n} < a_{n + 1}$ ，则称数列 ${a_{n}}$ 为“K数列”．关于命题：①存在等差数列 ${a_{n}}$ ，使得它是“K数列”；②若 ${a_{n}}$ 是首项为正数、公比为q的等比数列，则 $q \in [2 ， + \infty)$ 是 ${a_{n}}$ 为“K数列”的充要条件．下列判断正确的是（）

A、①和②都为真命题 B、①为真命题，②为假命题 C、①为假命题，②为真命题 D、①和②都为假命题

查看试题解析

三、解答题

17. 在 $△ A B C$ 中， $c o s A = - \frac{5}{13} ， c o s B = \frac{3}{5}$ ．

(1)、求 $s i n C$ 的值；

(2)、若 $A B = 4$ ，求 $△ A B C$ 的周长和面积．

查看试题解析
18. 如图，多面体 $A_{1} C_{1} D_{1} A B C D$ 是由棱长为3的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 沿平面 $A_{1} B C_{1}$ 截去一角所得到，在棱 $A_{1} C_{1}$ 上取一点E，过点 $D_{1}$ ， C，E的平面交棱 $B C_{1}$ 于点F．

(1)、求证： $E F ∥ A_{1} B$ ；

(2)、若 $C_{1} E = 2 E A_{1}$ ，求点E到平面 $A_{1} D_{1} C B$ 的距离以及 $E D_{1}$ 与平面 $A_{1} D_{1} C B$ 所成角的大小．

查看试题解析
19. 将某工厂的工人按年龄分成两组：“35周岁及以上”、“35周岁以下”，从每组中随机抽取80人，将他们的绩效分数分成5组： $[50 ， 60) ， [60 ， 70) ， [70 ， 80) ， [80 ， 90) ， [90 ， 100]$ ，分别加以统计，得到下列频率分布直方图．该工厂规定绩效分数不少于80者为生产标兵．
附： $χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ．
$P (x^{2} \geq k)$
0.100
0.050
0.010
0.001
k
2.706
3.841
6.635
10.828

(1)、请列出 $2 \times 2$ 列联表，并判断能否有 $95 %$ 的把握认为是否为生产标兵与工人所在的年龄组有关：

(2)、若已知该工厂工人中生产标兵的占比为 $30 %$ ，试估计该厂35周岁以下的工人所占的百分比以及生产标兵中35周岁以下的工人所占的百分比．

查看试题解析
20. 已知双曲线 $C$ 的中心在坐标原点，左焦点 $F_{1}$ 与右焦点 $F_{2}$ 都在 $x$ 轴上，离心率为 $3$ ，过点 $F_{2}$ 的动直线 $l$ 与双曲线 $C$ 交于点 $A$ 、 $B$ ．设 $\frac{| A F_{2} | \cdot | B F_{2} |}{{| A B |}^{2}} = λ$ ．

(1)、求双曲线 $C$ 的渐近线方程；

(2)、若点 $A$ 、 $B$ 都在双曲线 $C$ 的右支上，求 $λ$ 的最大值以及 $λ$ 取最大值时 $∠ A F_{1} B$ 的正切值；（关于求 $λ$ 的最值．某学习小组提出了如下的思路可供参考：①利用基本不等式求最值；②设 $\frac{| A F_{2} |}{| A B |}$ 为 $μ$ ，建立相应数量关系并利用它求最值；③设直线l的斜率为k，建立相应数量关系并利用它求最值）.

(3)、若点 $A$ 在双曲线 $C$ 的左支上（点 $A$ 不是该双曲线的顶点，且 $λ = 1$ ，求证： $△ A F_{1} B$ 是等腰三角形．且 $A B$ 边的长等于双曲线 $C$ 的实轴长的2倍．

查看试题解析
21. 三个互不相同的函数 $y = f (x) ， y = g (x)$ 与 $y = h (x)$ 在区间D上恒有 $f (x) \geq h (x) \geq g (x)$ 或恒有 $f (x) \leq h (x) \leq g (x)$ ，则称 $y = h (x)$ 为 $y = f (x)$ 与 $y = g (x)$ 在区间D上的“分割函数”．

(1)、设 $h_{1} (x) = 4 x ， h_{2} (x) = x + 1$ ，试分别判断 $y = h_{1} (x) 、 y = h_{2} (x)$ 是否是 $y = 2 x^{2} + 2$ 与 $y = - x^{2} + 4 x$ 在区间上的“分割函数”，请说明理由；

(2)、求所有的二次函数，使得该函数是 $y = 2 x^{2} + 2$ 与 $y = 4 x$ 在区间 $(- \infty ， + \infty)$ 上的“分割函数”；

(3)、若 $[m ， n] \subseteq [- 2 ， 2]$ ，且存在实数k，b，使得 $y = k x + b$ 为 $y = x^{4} - 4 x^{2}$ 与 $y = 4 x^{2} - 16$ 在区间 $[m ， n]$ 上的“分割函数”，求 $n - m$ 的最大值．

查看试题解析

$P (x^{2} \geq k)$	0.100	0.050	0.010	0.001
k	2.706	3.841	6.635	10.828