上海市奉贤区2023届高三数学二模试卷
试卷更新日期:2023-04-23 类型:高考模拟
一、填空题
-
1. 已知集合 , , 若 , 则 .2. 已知 , , 且 , 是虚数单位,则 .3. 在的展开式中,的系数为.(用数字作答)4. 已知圆柱的上、下底面的中心分别为、 , 过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的侧面积为 .5. 2017年5月某校高三年级1600名学生参加了教育局组织的期末统考,已知数学考试成绩 .(试卷满分为150分)统计结果显示数学考试成绩在80分到120分之间的人数约为总人数的 , 则此次统考中成绩不低于120分的学生人数约为.6. 已知两个正数 , 的几何平均值为1,则的最小值为 .7. 某种动物从出生起活到20岁的概率为0.8,从出生起活到25岁的概率为0.4,现有一个20岁的这种动物,它能活到25岁的概率为.8. 已知随机变量的分布为 , 且 , 若 , 则实数 .9. 设圆与双曲线的一条渐近线相切,则该双曲线的渐近线方程为 .10. 内角 的对边分别为 ,若 的面积为 ,则11. 在集合中任取一个偶数和一个奇数构成一个以原点为起点的向量 , 从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,面积不超过4的平行四边形的个数是 .12. 已知为上的奇函数,且当时, , 则的驻点为 .
二、单选题
-
13. “”是“直线与垂直”的A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件14. 下列函数中,以为周期且在区间 单调递增的是( )A、 B、 C、 D、15. 某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据 得到下面的散点图:

由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A、 B、 C、 D、16. 设是一个无穷数列的前项和,若一个数列满足对任意的正整数 , 不等式恒成立,则称数列为和谐数列,有下列3个命题:①若对任意的正整数均有 , 则为和谐数列;
②若等差数列是和谐数列,则一定存在最小值;
③若的首项小于零,则一定存在公比为负数的一个等比数列是和谐数列.
以上3个命题中真命题的个数有( )个
A、0 B、1 C、2 D、3三、解答题
-
17. 已知等差数列的公差不为零, , 且 , , 成等比数列.(1)、求的通项公式;(2)、计算 .18. 如图,在四棱锥中, , 且 .
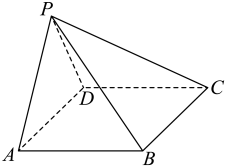 (1)、证明:平面平面;(2)、若 , , 且四棱锥的体积为 , 求与平面所成的线面角的大小.19. 设函数的定义域是R,它的导数是 . 若存在常数 , 使得对一切恒成立,那么称函数具有性质 .(1)、求证:函数不具有性质;(2)、判别函数是否具有性质 . 若具有求出的取值集合;若不具有请说明理由.20. 某小区有块绿地,绿地的平面图大致如下图所示,并铺设了部分人行通道.
(1)、证明:平面平面;(2)、若 , , 且四棱锥的体积为 , 求与平面所成的线面角的大小.19. 设函数的定义域是R,它的导数是 . 若存在常数 , 使得对一切恒成立,那么称函数具有性质 .(1)、求证:函数不具有性质;(2)、判别函数是否具有性质 . 若具有求出的取值集合;若不具有请说明理由.20. 某小区有块绿地,绿地的平面图大致如下图所示,并铺设了部分人行通道.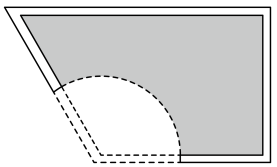
为了简单起见,现作如下假设:
假设1:绿地是由线段 , , , 和弧围成的,其中是以点为圆心,圆心角为的扇形的弧,见图1;
假设2:线段 , , , 所在的路行人是可通行的,圆弧暂时未修路;
假设3:路的宽度在这里暂时不考虑;
假设4:路用线段或圆弧表示,休息亭用点表示.
图1-图3中的相关边、角满足以下条件:
直线与的交点是 , , . 米.
小区物业根据居民需求,决定在绿地修建一个休息亭.根据不同的设计方案解决相应问题,结果精确到米.
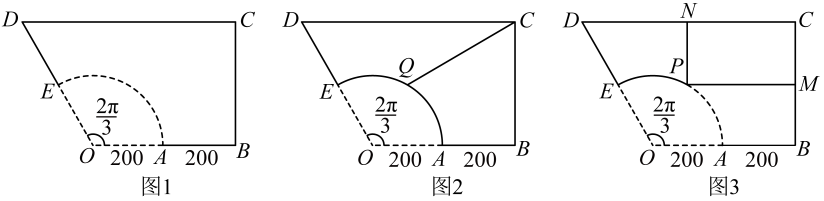 (1)、假设休息亭建在弧的中点,记为 , 沿和线段修路,如图2所示.求的长;(2)、假设休息亭建在弧上的某个位置,记为 , 作交于 , 作交于 . 沿、线段和线段修路,如图3所示.求修建的总路长的最小值;(3)、请你对(1)和(2)涉及到的两种设计方案做个简明扼要的评价.21. 已知椭圆: , , . 椭圆内部的一点 , 过点作直线交椭圆于 , 作直线交椭圆于 . 、是不同的两点.(1)、若椭圆的离心率是 , 求的值;(2)、设的面积是 , 的面积是 , 若 , 时,求的值;(3)、若点 , 满足且 , 则称点在点的左上方.求证:当时,点在点的左上方.
(1)、假设休息亭建在弧的中点,记为 , 沿和线段修路,如图2所示.求的长;(2)、假设休息亭建在弧上的某个位置,记为 , 作交于 , 作交于 . 沿、线段和线段修路,如图3所示.求修建的总路长的最小值;(3)、请你对(1)和(2)涉及到的两种设计方案做个简明扼要的评价.21. 已知椭圆: , , . 椭圆内部的一点 , 过点作直线交椭圆于 , 作直线交椭圆于 . 、是不同的两点.(1)、若椭圆的离心率是 , 求的值;(2)、设的面积是 , 的面积是 , 若 , 时,求的值;(3)、若点 , 满足且 , 则称点在点的左上方.求证:当时,点在点的左上方.