陕西省西安市临潼区、阎良区2023届高三理数一模试卷
试卷更新日期:2023-04-23 类型:高考模拟
一、单选题
-
1. 集合 , , 则( )A、 B、 C、 D、2. 已知是虚数单位,复数 , 则复数z的共轭复数为( )A、2 B、-2 C、2 D、23. 为了提高学生综合能力,某高校每年安排大三学生在暑假期间进行社会实践活动,现将8名学生平均分配给甲,乙两家单位,其中两名外语系学生不能分给同一家单位;另三名艺术系学生也不能同时分给同一家单位,其余学生随机分配,则不同的分配方案有( )A、114种 B、38种 C、108种 D、36种4. 已知 , 则θ等于( )A、 B、 C、 D、5. 已知 , 向量与向量垂直, , , 2成等比数列,则与的等差中项为( )A、 B、 C、 D、16. 函数是定义在上的奇函数,且在上单调递增, , 则不等式的解集为( )A、 B、 C、 D、7. 已知分别是双曲线的左、右焦点,为双曲线右支上的任意一点且 , 则双曲线离心率的取值范围是( )A、(1,2] B、[2 +) C、(1,3] D、[3,+)8. 在R上定义运算 , 若关于x的不等式的解集是集合的子集,则实数a的取值范围为( )A、 B、 C、 D、9. 函数的图象大致为( )A、
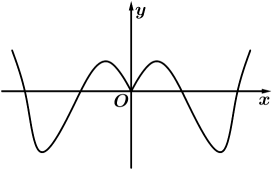 B、
B、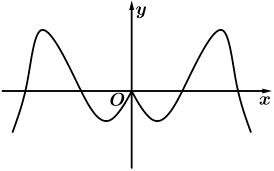 C、
C、 D、
D、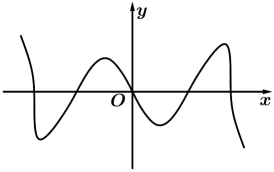 10. 数列的前项和为 , , 若该数列满足 , 则下列命题中错误的是( )A、是等差数列 B、 C、 D、是等比数列11. 定义在上的单调函数 , 若对任意实数 , 都有 , 若是方程的一个解,则可能存在的区间是( )A、 B、 C、 D、12. 已知 , 分别为双曲线的左、右焦点,且 , 点P为双曲线右支上一点,M为的内心,若成立,则λ的值为( )
10. 数列的前项和为 , , 若该数列满足 , 则下列命题中错误的是( )A、是等差数列 B、 C、 D、是等比数列11. 定义在上的单调函数 , 若对任意实数 , 都有 , 若是方程的一个解,则可能存在的区间是( )A、 B、 C、 D、12. 已知 , 分别为双曲线的左、右焦点,且 , 点P为双曲线右支上一点,M为的内心,若成立,则λ的值为( )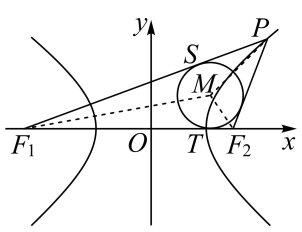 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
13. 二项式的展开式中,项的系数为 .14. 在中,点D是边BC上一点,且 , . , , 则DC=.
 15. 空间四边形ABCD中,AC与BD是四边形的两条对角线,M,N分别为线段AB,CD上的两点,且满足 , , 若点G在线段MN上,且满足 , 若向量满足 , 则 .16. 表面积为100π的球面上有四点S、A、B、C,△ABC是等边三角形,球心O到平面ABC的距离为3,若面SAB⊥面ABC,则棱锥体积的最大值为.
15. 空间四边形ABCD中,AC与BD是四边形的两条对角线,M,N分别为线段AB,CD上的两点,且满足 , , 若点G在线段MN上,且满足 , 若向量满足 , 则 .16. 表面积为100π的球面上有四点S、A、B、C,△ABC是等边三角形,球心O到平面ABC的距离为3,若面SAB⊥面ABC,则棱锥体积的最大值为.
三、解答题
-
17. 已知函数 .(1)、求函数的单调递减区间及对称轴方程;(2)、若在中,角A,B、C所对的边分别为a,b,c,且 , , 求面积的最大值.18. 在四棱锥中, , , , , .
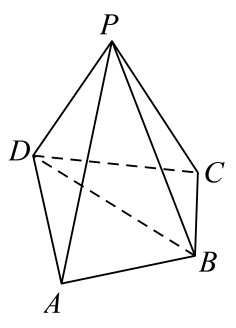 (1)、求证:平面平面;(2)、求平面与平面所成角的余弦值.19. 甲乙二人均为射击队S中的射击选手,某次训练中,二人进行了100次“对抗赛”,每次“对抗赛”中,二人各自射击一次,并记录二人射击的环数,更接近10环者获胜,环数相同则记为“平局”.已知100次对抗的成绩的频率分布如下:
(1)、求证:平面平面;(2)、求平面与平面所成角的余弦值.19. 甲乙二人均为射击队S中的射击选手,某次训练中,二人进行了100次“对抗赛”,每次“对抗赛”中,二人各自射击一次,并记录二人射击的环数,更接近10环者获胜,环数相同则记为“平局”.已知100次对抗的成绩的频率分布如下:“对抗赛”成绩(甲:乙)
总计
频数
21
13
6
25
15
10
4
2
4
100
这100次“对抗赛”中甲乙二人各自击中各环数的频率可以视为相应的概率.
附:参考公式:
参考数据:
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
(1)、设甲,乙两位选手各自射击一次,得到的环数分别为随机变量X,Y,求 , , , .(2)、若某位选手在一次射击中命中9环或10环,则称这次射击成绩优秀,以这100次对抗赛的成绩为观测数据,能否在犯错误的概率不超过0.01的前提下认为甲的射击成绩优秀与乙的射击成绩优秀有关联?(3)、在某次团队赛中,射击队S只要在最后两次射击中获得至少19环即可夺得此次比赛的冠军,现有以下三种方案:方案一:由选手甲射击2次﹔
方案二:由选手甲、乙各射击1次;
方案三:由选手乙射击2次.
则哪种方案最有利于射击队S夺冠?请说明理由.
20. 在椭圆C: , , 过点与的直线的斜率为 .(1)、求椭圆C的标准方程;(2)、设F为椭圆C的右焦点,P为直线上任意一点,过F作PF的垂线交椭圆C于M,N两点,当取最大值时,求直线MN的方程.