陕西省2023届高三下学期理数教学质量检测试卷（二）

试卷更新日期：2023-04-23 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} + 2 x - 3 > 0}$ ， $B = {- 1 ， 0 ， 1 ， 2}$ ，则（）

A、 $A \cap B = {2}$ B、 $A ∪ B = R$ C、 $B ∩ (∁_{R} A) = {- 1 ， 0}$ D、 $B \cup (∁_{R} A) = {x | - 3 < x < 1}$

查看试题解析
2. 定义：若复数 $z$ 与 $z^{'}$ 满足 $z \cdot z^{'} = 1$ ，则称复数 $z$ 与 $z^{'}$ 互为倒数.已知复数 $z = \frac{1}{2} + \frac{\sqrt{3}}{2} i$ ，则复数 $z$ 的倒数 $z^{^{'}} =$ （）

A、 $\frac{1}{2} - \frac{\sqrt{3}}{2} i$ B、 $\frac{1}{2} + \frac{\sqrt{3}}{2} i$ C、 $- \frac{1}{2} - \frac{\sqrt{3}}{2} i$ D、 $- \frac{1}{2} + \frac{\sqrt{3}}{2} i$

查看试题解析
3. 设 $\vec{a} = (3 ， m)$ ， $\vec{b} = (4 ， 2)$ ，则“ $m = - 1$ ”是“ $\vec{a} ⊥ (\vec{a} - \vec{b})$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. $A$ ， $B$ ， $C$ ， $D$ 四人之间进行投票，各人投自己以外的人 $1$ 票的概率都是 $\frac{1}{3}$ （个人不投自己的票），则仅 $A$ 一人是最高得票者的概率为（）

A、 $\frac{1}{27}$ B、 $\frac{4}{81}$ C、 $\frac{5}{27}$ D、 $\frac{8}{81}$

查看试题解析
5. 短道速滑队6名队员(含赛前系列赛积分最靠前的甲乙丙三名队员在内)进行冬奥会选拔，记“甲得第一名”为p，“乙得第二名”为q，“丙得第三名”为r，若 $p \lor q$ 是真命题， $p \land q$ 是假命题， $(\neg q) \land r$ 是真命题，则选拔赛的结果为（）

A、甲得第一名，乙得第二名，丙得第三名 B、甲得第二名，乙得第一名，丙得第三名 C、甲得第一名，乙得第三名，丙得第二名 D、甲得第一名，乙没得第二名，丙得第三名

查看试题解析
6. 我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”如图所示的程序框图反映了对此题的一个求解算法，则输出的 $n =$ （）

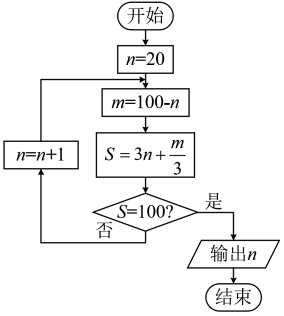A、25 B、45 C、55 D、75

查看试题解析
7. 已知等比数列 ${a_{n}}$ 的前n项和与前n项积分别为 $S_{n}$ ， $T_{n}$ ，公比为正数，且 $a_{3} = 16$ ， $S_{3} = 112$ ，则使 $T_{n} > 1$ 成立的n的最大值为（）

A、8 B、9 C、12 D、13

查看试题解析
8. 已知函数 $f (x) = 2 c o s (ω x + φ) (ω > 0 ， 0 < φ < \frac{π}{2})$ 的图象的相邻两条对称轴间的距离为 $2 π$ ， $f (0) = 1$ ．则下列选项正确的是（）

A、 $ω = \frac{π}{2}$ B、 $f (x)$ 的图象的对称轴方程为 $x = k π - \frac{2 π}{3}$ （ $k \in Z$ ） C、 $f (x)$ 的单调递减区间为 $[k π - \frac{π}{6} ， k π + \frac{π}{3}]$ （ $k \in Z$ ） D、 $f (x) \geq 1$ 的解集为 $[4 k π - \frac{4 π}{3} ， 4 k π]$ （ $k \in Z$ ）

查看试题解析
9. 在 ${(3 x + \frac{1}{x})}^{n}$ 的展开式中，各项系数和与二项式系数和之比为 $64 ： 1$ ，则展开式中常数项为（）

A、540 B、480 C、320 D、160

查看试题解析
10. 已知三棱锥 $P - A B C$ 中， $A C = B C = 1$ ， $A C ⊥ B C$ ， D是 $A B$ 的中点， $P D ⊥$ 平面ABC，点P，A，B，C在球心为O的球面上，若三棱锥 $P - A B C$ 的体积是 $\frac{1}{6}$ ，则球O的半径为（）

A、 $\frac{3}{2}$ B、1 C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
11. 如图， $F_{1}$ ， $F_{2}$ 分别为椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点，点 $P$ 在椭圆上， $△ P O F_{2}$ 是面积为 $4 \sqrt{3}$ 的正三角形，则 $e$ 的值是（）

A、 $\sqrt{2} - 1$ B、 $\sqrt{3} - 1$ C、 $\sqrt{3}$ D、 $4 - 2 \sqrt{3}$

查看试题解析
12. 已知集合 $M = {α | f (α) = 0}$ ， $N = {β | g (β) = 0}$ .若存在 $α \in M$ ， $β \in N$ ，使 $| α - β | < n$ ，则称函数 $f (x)$ 与 $g (x)$ 互为“n度零点函数”若函数 $f (x) = e^{2 - x} - 1$ 与函数 $g (x) = x^{2} - a e^{x}$ 互为“1度零点函数”，则实数a的取值范围为（）

A、 $(\frac{1}{e} ， \frac{4}{e^{2}}]$ B、 $(\frac{1}{e^{2}} ， \frac{4}{e^{2}}]$ C、 $[\frac{4}{e^{2}} ， \frac{2}{e})$ D、 $[\frac{1}{e^{3}} ， \frac{2}{e^{2}})$

查看试题解析

二、填空题

13. 某产品的广告费用x与销售额y的统计数据如下表：
广告费x（万元）
2
3
4
5
利润y（万元）
26
m
49
54
根据上表可得回归方程为 $\hat{y} = 9.4 x + 9.1$ ，表中有一数据模糊不清，请推算该数据的值为．

查看试题解析
14. 在 $△ A B C$ 中，角A，B，C的对边分别为a，b，c，且 $a c o s C + \sqrt{3} a s i n C - b - c = 0$ ．若 $△ A B C$ 的面积为 $3 \sqrt{3}$ ，则 $b + c$ 的最小值为．

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} 2 e^{x - 1} ， x < 1 \\ x^{3} + x ， x \geq 1 \end{array}$ ，则 $f (f (x)) < 2$ 的解集为．

查看试题解析
16. 如图，两个椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ 、 $\frac{y^{2}}{25} + \frac{x^{2}}{9} = 1$ 内部重叠区域的边界记为曲线 $C ， P$ 是曲线 $C$ 上的任意一点，给出下列四个判断：
① $P$ 到 $F_{1} (- 4 ， 0)$ 、 $F_{2} (4 ， 0)$ 、 $E_{1} (0 ， - 4)$ 、 $E_{2} (0 ， 4)$ 四点的距离之和为定值；
②曲线 $C$ 关于直线 $y = x ， y = - x$ 均对称；
③曲线 $C$ 所围区域面积必小于36．
④曲线 $C$ 总长度不大于6π．上述判断中正确命题的序号为．

查看试题解析

三、解答题

17. 已知在各项均为正数的等差数列 ${a_{n}}$ 中， $a_{2} + a_{3} + a_{4} = 21$ ，且 $a_{2} - 1$ ， $a_{3} + 1$ ， $a_{4} + a_{3}$ 构成等比数列 ${b_{n}}$ 的前三项.

(1)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、设数列 $c_{n} =$ ___________，求数列 ${c_{n}}$ 的前 $n$ 项和 $S_{n}$ .请在① $a_{n} b_{n}$ ；② $\frac{b_{n}}{(b_{n} - 1) (b_{n + 1} - 1)}$ ；③ $(- 1)^{n} a_{n} + n$ 这三个条件中选择一个，补充在上面的横线上，并完成解答.

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中， $A B / / C D$ ， $∠ A B C = 90 °$ ， $A B = B C = 1$ ， △ $P D C$ 是边长为2的等边三角形，平面 $P D C ⊥$ 平面 $A B C D$ ， $E$ 为线段 $P C$ 上一点.

(1)、设平面 $P A B \cap$ 平面 $P D C = l$ ，证明： $l / /$ 平面 $A B C D$ ；

(2)、是否存在这样点 $E$ ，使平面 $A D E F$ 与平面 $A B C D$ 所成角为 $60 °$ ，如果存在，求 $\frac{| C E |}{| C P |}$ 的值；如果不存在，请说明理由.

查看试题解析
19. 如图，椭圆 $E$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 内切于矩形 $A B C D$ ，其中 $A B$ ， $C D$ 与 $x$ 轴平行，直线 $A C$ ， $B D$ 的斜率之积为 $- \frac{1}{2}$ ，椭圆的焦距为2.

(1)、求椭圆 $E$ 的标准方程；

(2)、椭圆上的点 $P$ ， $Q$ 满足直线 $O P$ ， $O Q$ 的斜率之积为 $- \frac{1}{2}$ ，其中 $O$ 为坐标原点.若 $M$ 为线段 $P Q$ 的中点，则 ${| M O |}^{2} + {| M Q |}^{2}$ 是否为定值？如果是，求出该定值；如果不是，说明理由.

查看试题解析
20. 为降低工厂废气排放量，某厂生产甲、乙两种不同型号的减排器，现分别从甲、乙两种减排器中各自抽取100件进行性能质量评估检测，综合得分情况的频率分布直方图如图所示．
减排器等级分布如表．
综合得分k的范围
减排器等级
$k \geq 85$
一级品
$75 \leq k < 85$
二级品
$70 \leq k < 75$
三级品

(1)、若从这100件甲型号减排器中按等级用分层抽样的方法抽取10件，再从这10件产品中随机抽取4件，求至少有2件一级品的概率；

(2)、将频率分布直方图中的频率近似地看作概率，用样本估计总体，若从乙型号减排器中随机抽取3件，求二级品数 $ξ$ 的分布列及数学期望 $E (ξ)$ ．

查看试题解析
21. 已知函数 $f (x) = \frac{1}{2} (x + a)^{2} + b l n x + 2$ ， $a 、 b \in R$ ．

(1)、当 $a = 0$ 时，设函数 $f (x)$ 在区间 $[1 ， 2]$ 上的最小值为 $g (b)$ ，求 $m a x {g (b)}$ ；

(2)、设 $b = 1$ ，若函数 $f (x)$ 有两个极值点 $x_{1} ， x_{2}$ ，且 $x_{1} < x_{2}$ ，求证： $5 x_{1} - 2 f (x_{2}) < 0$ ．

查看试题解析
22. 在直角坐标系xOy中，直线 $l$ 的参数方程为 ${\begin{array}{l} x = \frac{\sqrt{2}}{2} t ， \\ y = 1 - \frac{\sqrt{2}}{2} t ， \end{array}$ （t为参数）．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为 $ρ^{2} (1 + 3 s i n^{2} θ) = 4$ ．

(1)、写出直线 $l$ 的普通方程和曲线C的直角坐标方程；

(2)、若直线 $l$ 与曲线C交于P，Q两点，PQ中点为M，A（1，0），求 $\frac{| A P | + | A Q |}{| A M |}$ 的值．

查看试题解析
23. 已知a，b，c为正实数且 $a + 2 b + 3 c = 5$ ．

(1)、求 $a^{2} + b^{2} + c^{2}$ 的最小值；

(2)、当 $\sqrt{2 a b} + \sqrt{3 a c} + \sqrt{6 b c} \geq 5$ 时，求a+b+c的值．

查看试题解析

综合得分k的范围	减排器等级
$k \geq 85$	一级品
$75 \leq k < 85$	二级品
$70 \leq k < 75$	三级品

广告费x（万元）	2	3	4	5
利润y（万元）	26	m	49	54