广东省茂名市2023届高三数学二模试卷

试卷更新日期：2023-04-23 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | | x | \leq 1}$ ， $B = {x | 2 x - a < 0}$ ，若 $A ⊆ B$ ，则实数 $a$ 的取值范围是（）

A、 $(2 ， + ∞)$ B、 $[2 ， + \infty)$ C、 $(- \infty ， 2)$ D、 $(- \infty ， 2]$

查看试题解析
2. 若复数 $z$ 满足 $i \cdot z = 4 + 3 i$ ，则 $| z | =$ （）

A、2 B、 $\sqrt{5}$ C、3 D、5

查看试题解析
3. 已知平面α ，直线m ， n满足m $⊄$ α ， n $\subset$ α ，则“m∥n”是“m∥α”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 从1、2、3、4、5中任选3个不同数字组成一个三位数，则该三位数能被3整除的概率为（）

A、 $\frac{1}{10}$ B、 $\frac{1}{5}$ C、 $\frac{3}{10}$ D、 $\frac{2}{5}$

查看试题解析
5. 已知平面 $x O y$ 内的动点 $P$ ，直线 $l$ ： $x s i n θ + y c o s θ = 1$ ，当 $θ$ 变化时点 $P$ 始终不在直线 $l$ 上，点 $Q$ 为 $⊙ C$ ： $x^{2} + y^{2} - 8 x - 2 y + 16 = 0$ 上的动点，则 $| P Q |$ 的取值范围为（）

A、 $(\sqrt{17} - 2 ， \sqrt{17})$ B、 $(\sqrt{17} - 2 ， \sqrt{17} + 2]$ C、 $[\sqrt{17} - 2 ， \sqrt{17} + 2)$ D、 $(\sqrt{17} - 2 ， \sqrt{17} + 2)$

查看试题解析
6. 如图所示，正三棱锥 $P - A B C$ ，底面边长为2，点Р到平面ABC距离为2，点M在平面PAC内，且点M到平面ABC的距离是点P到平面ABC距离的 $\frac{2}{3}$ ，过点M作一个平面，使其平行于直线PB和AC，则这个平面与三棱锥表面交线的总长为（）

A、 $\frac{24 + 16 \sqrt{3}}{9}$ B、 $\frac{12 + 16 \sqrt{3}}{9}$ C、 $\frac{12 + 8 \sqrt{3}}{9}$ D、 $\frac{24 + 8 \sqrt{3}}{9}$

查看试题解析
7. 黎曼函数 $R (x)$ 是由德国数学家黎曼发现并提出的，它是一个无法用图象表示的特殊函数，此函数在高等数学中有着广泛的应用， $R (x)$ 在 $[0 ， 1]$ 上的定义为：当 $x = \frac{q}{p}$ （ $p > q$ ，且p，q为互质的正整数）时， $R (x) = \frac{1}{p}$ ；当 $x = 0$ 或 $x = 1$ 或 $x$ 为 $(0 ， 1)$ 内的无理数时， $R (x) = 0$ ，则下列说法错误的是（）

A、 $R (x)$ 在 $[0 ， 1]$ 上的最大值为 $\frac{1}{2}$ B、若 $a ， b \in [0 ， 1]$ ，则 $R (a \cdot b) \geq R (a) \cdot R (b)$ C、存在大于1的实数 $m$ ，使方程 $R (x) = \frac{m}{m + 1} (x \in [0 ， 1])$ 有实数根 D、 $\forall x \in [0 ， 1]$ ， $R (1 - x) = R (x)$

查看试题解析
8. 已知函数 $f (x) = 2 s i n x c o s x + 4 c o s^{2} x - 1$ ，若实数a、b、c使得 $a f (x) - b f (x + c) = 3$ 对任意的实数 $x$ 恒成立，则 $2 a + b - c o s c$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析

二、多选题

9. 小爱同学在一周内自测体温（单位：℃）依次为36.1，36.2，36.1，36.5，36.3，36.6，36.3，则该组数据的（）

A、平均数为36.3 B、方差为0.04 C、中位数为36.3 D、第80百分位数为36.55

查看试题解析
10. 已知 $O$ 为坐标原点，椭圆 $C$ ： $\frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，椭圆的上顶点和右顶点分别为A、B，点P、Q都在 $C$ 上，且 $\vec{P O} = \vec{O Q}$ ，则下列说法正确的是（）

A、 $△ P Q F_{2}$ 周长的最小值为14 B、四边形 $P F_{1} Q F_{2}$ 可能是矩形 C、直线 $P B$ ， $Q B$ 的斜率之积为定值 $- \frac{9}{16}$ D、 $△ P Q F_{2}$ 的面积最大值为 $3 \sqrt{7}$

查看试题解析
11. 已知 $f (x) = {\begin{array}{l} - x^{2} + 2 x + 1 ， x < 0 \\ \frac{x}{e^{x}} ， x \geq 0 \end{array}$ ，若关于 $x$ 的方程 $4 e f^{2} (x) - a f (x) + \frac{1}{e} = 0$ 恰好有6个不同的实数解，则 $a$ 的取值可以是（）

A、 $\frac{17}{4}$ B、 $\frac{19}{4}$ C、 $\frac{21}{4}$ D、 $\frac{23}{4}$

查看试题解析
12. 如图所示，有一个棱长为4的正四面体 $P - A B C$ 容器，D是PB的中点，E是CD上的动点，则下列说法正确的是（）

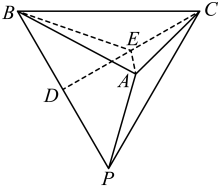A、若E是CD的中点，则直线AE与PB所成角为 $\frac{π}{2}$ B、 $△ A B E$ 的周长最小值为 $4 + \sqrt{34}$ C、如果在这个容器中放入1个小球（全部进入），则小球半径的最大值为 $\frac{\sqrt{6}}{3}$ D、如果在这个容器中放入10个完全相同的小球（全部进入），则小球半径的最大值为 $\sqrt{6} - 2$

查看试题解析

三、填空题

13. 已知实数a，b满足 $l g a + l g b = l g (a + 2 b)$ ，则 $a + b$ 的最小值是.

查看试题解析
14. 已知函数 $f (x)$ 的图像关于直线 $x = 1$ 对称，且 $x \leq 1$ 时， $f (x) = e^{x} + x - 1$ ，则曲线 $y = f (x)$ 在点 $P (2 ， f (2))$ 处的切线方程为.

查看试题解析
15. 已知抛物线 $y^{2} = 6 x$ 的焦点为 $F$ ，准线为 $l$ ，过 $F$ 的直线与抛物线交于点A、B，与直线 $l$ 交于点D，若 $\vec{A F} = λ \vec{F B} (λ > 1)$ 且 $| \vec{B D} | = 4$ ，则 $λ =$ .

查看试题解析
16. 修建栈道是提升旅游观光效果的一种常见手段.如图，某水库有一个半径为1百米的半圆形小岛，其圆心为C且直径MN平行坝面.坝面上点A满足 $A C ⊥ M N$ ，且AC长度为3百米，为便于游客到小岛观光，打算从点A到小岛建三段栈道AB、BD与BE，水面上的点B在线段AC上，且BD、BE均与圆C相切，切点分别为D、E，其中栈道AB、BD、BE和小岛在同一个平面上.此外在半圆小岛上再修建栈道 $\overset{⌢}{M E}$ 、 $\overset{⌢}{D N}$ 以及MN，则需要修建的栈道总长度的最小值为百米.

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 的前 $n (n \in N^{*})$ 项和 $S_{n}$ 满足 $S_{n + 1} + S_{n} = 2 {(n + 1)}^{2}$ ，且 $a_{1} = 1$ .

(1)、求 $a_{2}$ ， $a_{3}$ ， $a_{4}$ ；

(2)、若 $S_{n}$ 不超过240，求 $n$ 的最大值.

查看试题解析
18. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c，且满足 $t a n B = \frac{s i n (C + \frac{π}{3})}{s i n (C - \frac{π}{6})}$ .

(1)、求A；

(2)、若D为边BC上一点，且 $2 C D = A D = B D$ ，试判断 $△ A B C$ 的形状.

查看试题解析
19. 在四棱锥 $P - A B C D$ 中，平面 $P A D ⊥$ 平面 $A B C D$ ， $P A = P D$ ， $O$ 为 $A D$ 的中点.

(1)、求证： $P O ⊥ B C$ ；

(2)、若 $A B / / C D$ ， $A B = 8$ ， $A D = D C = C B = 4$ ， $P O = 2 \sqrt{7}$ ，点 $E$ 在棱 $P B$ 上，直线 $A E$ 与平面 $A B C D$ 所成角为 $\frac{π}{6}$ ，求点 $E$ 到平面 $P C D$ 的距离.

查看试题解析
20. 已知 $F_{1}$ ， $F_{2}$ 分别为双曲线 $E$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点，Р为渐近线上一点，且 $\sqrt{3} | P F_{1} | = \sqrt{7} | P F_{2} |$ ， $c o s ∠ F_{1} P F_{2} = \frac{\sqrt{21}}{7}$ .

(1)、求双曲线的离心率；

(2)、若双曲线E实轴长为2，过点 $F_{2}$ 且斜率为 $k$ 的直线 $l$ 交双曲线C的右支不同的A，B两点， $Q$ 为 $x$ 轴上一点且满足 $| Q A | = | Q B |$ ，试探究 $\frac{2 | Q F_{2} |}{| A F_{1} | + | B F_{1} | - 4}$ 是否为定值，若是，则求出该定值；若不是，请说明理由.

查看试题解析
21. 已知函数 $f (x) = \frac{x^{2}}{2} + l n x - 2 a x$ ， $a$ 为常数，且 $a > 0$ .

(1)、判断 $f (x)$ 的单调性；

(2)、当 $0 < a < 1$ 时，如果存在两个不同的正实数 $m$ ， $n$ 且 $f (m) + f (n) = 1 - 4 a$ ，证明： $m + n > 2$ .

查看试题解析
22. 马尔可夫链是因俄国数学家安德烈·马尔可夫得名，其过程具备“无记忆”的性质，即第 $n + 1$ 次状态的概率分布只跟第 $n$ 次的状态有关，与第 $n - 1 ， n - 2 ， n - 3 ， \cdot \cdot \cdot$ 次状态是“没有任何关系的”.现有甲、乙两个盒子，盒子中都有大小、形状、质地相同的2个红球和1个黑球.从两个盒子中各任取一个球交换，重复进行 $n (n \in N^{*})$ 次操作后，记甲盒子中黑球个数为 $X_{n}$ ，甲盒中恰有1个黑球的概率为 $a_{n}$ ，恰有2个黑球的概率为 $b_{n}$ .

(1)、求 $X_{1}$ 的分布列；

(2)、求数列 ${a_{n}}$ 的通项公式；

(3)、求 $X_{n}$ 的期望.

查看试题解析