安徽省(九师联盟)2023届数学二模试卷
试卷更新日期:2023-04-21 类型:高考模拟
一、单选题
-
1. 已知全集 , 集合 , 则集合等于( )A、 B、 C、 D、2. 已知平面向量 , , 若与垂直,则实数( )A、2 B、1 C、-1 D、-23. 在一些比赛中,对评委打分的处理方法一般是去掉一个最高分,去掉一个最低分,然后计算余下评分的均值作为参赛者的得分.在一次有9位评委参加的赛事中,评委对一名参赛者所打的9个分数,去掉一个最高分,去掉一个最低分后,一定不变的数字特征为( )A、平均值 B、中位数 C、众数 D、方差4. 已知数列的前项和为 , 若 , 则( )A、-2023 B、 C、 D、20235. 昆虫信息素是昆虫用来表示聚集、觅食、交配、警戒等信息的化学物质,是昆虫之间起化学通讯作用的化合物,是昆虫交流的化学分子语言,包括利它素、利己素、协同素、集合信息素、追踪信息素、告警信息素、疏散信息素、性信息素等.人工合成的昆虫信息素在生产中有较多的应用,尤其在农业生产中的病虫害的预报和防治中较多使用.研究发现,某昆虫释放信息素t秒后,在距释放处x米的地方测得的信息素浓度y满足 , 其中k,a为非零常数.已知释放信息素1秒后,在距释放处2米的地方测得信息素浓度为m;若释放信息素4秒后,距释放处b米的位置,信息素浓度为 , 则b=( )A、3 B、4 C、5 D、66. 巴普士(约公元3~4世纪),古希腊亚历山大学派著名几何学家.生前有大量的著作,但大部分遗失在历史长河中,仅有《数学汇编》保存下来.《数学汇编》一共8卷,在《数学汇编》第3卷中记载着这样一个定理:“如果在同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于该闭合图形的面积与该闭合图形的重心旋转所得周长的积”,(表示平面闭合图形绕旋转轴旋转所得几何体的体积,S表示闭合图形的面积,l表示重心绕旋转轴旋转一周的周长).已知在梯形ABCD中, , , , 利用上述定理可求得梯形ABCD的重心G到点B的距离为( )
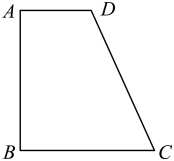 A、 B、 C、 D、7. 已知双曲线的左、右焦点分别为 , , P是圆()与的一个交点,若的内切圆的半径为a,则的离心率为( )A、 B、 C、2 D、8. 已知 , , , 则( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知双曲线的左、右焦点分别为 , , P是圆()与的一个交点,若的内切圆的半径为a,则的离心率为( )A、 B、 C、2 D、8. 已知 , , , 则( )A、 B、 C、 D、二、多选题
-
9. 设为复数,则下列命题中一定成立的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么10. 已知函数 , 则( )A、的图象关于点对称 B、为的一个周期 C、的值域为 D、在上单调递减11. 已知抛物线的焦点为 , 直线与抛物线交于两点,是线段的中点,过作轴的垂线交抛物线于点 , 则下列判断正确的是( )A、若过点 , 则的准线方程为 B、若过点 , 则 C、若 , 则 D、若 , 则点的坐标为12. 定义区间 , , , 的长度为.如果一个函数的所有单调递增区间的长度之和为常数(其中 , 为自然对数的底数),那么称这个函数为“函数”,则( )A、是“函数” B、是“函数” C、是“函数”,且 D、是“函数”,且
三、填空题
-
13. 已知函数(且),曲线在处的切线与直线垂直,则 .14. 的展开式中的常数项为 . (用数字作答)15. 在正三棱柱中,D为棱AB的中点,与交于点E,若 , 则CD与所成角的余弦值为 .
 16. 已知 , 则关于x的方程有6个互不相等的实数解的充要条件为 .
16. 已知 , 则关于x的方程有6个互不相等的实数解的充要条件为 .四、解答题
-
17. 在中,角的对边分别为 , 且.(1)、求的大小;(2)、若 , , 求的面积.18. 在数列中, , 当时,(1)、求证:为等比数列;(2)、若 , 求{}的前n项和 .19. 如图,在四棱锥中,底面ABCD是边长为4的正方形,E为PA的中点,过E与底面ABCD平行的平面与棱PC,PD分别交于点G,F,M在线段AE上,且 .
 (1)、求证:BG//平面;(2)、若PA⊥平面ABCD,且 , 求平面CFM与平面PCD所成锐二面角的余弦值.20. 现在世界正处于百年未见之大变局,我国面临着新的考验,为增强学生的爱国意识和凝聚力,某学校高二年级组织举办了“中国国情和当今世界局势”的知识对抗竞赛,主要是加深对新中国成立以来我国在经济建设、科技创新、精神文明建设等方面取得的成就和最新世界经济、政治时事的了解.组织者按班级将参赛人员随机分为若干组,每组均为两名选手,每组对抗赛开始时,组织者随机从准备好的题目中抽取2道试题供两位选手抢答,每位选手抢到每道试题的机会相等.比赛得分规则为:选手抢到试题且回答正确得10分,对方选手得0分;选手抢到试题但回答错误或没有回答得0分,对方选手得5分;2道题目抢答完毕后得分多者获胜.已知甲、乙两名选手被分在同一组进行对抗赛,每道试题甲回答正确的概率为 , 乙回答正确的概率为 , 两名选手回答每道试题是否正确相互独立.2道试题抢答后的各自得分作为两位选手的个人总得分.(1)、求乙总得分为10分的概率;(2)、记X为甲的总得分,求X的分布列和数学期望.
(1)、求证:BG//平面;(2)、若PA⊥平面ABCD,且 , 求平面CFM与平面PCD所成锐二面角的余弦值.20. 现在世界正处于百年未见之大变局,我国面临着新的考验,为增强学生的爱国意识和凝聚力,某学校高二年级组织举办了“中国国情和当今世界局势”的知识对抗竞赛,主要是加深对新中国成立以来我国在经济建设、科技创新、精神文明建设等方面取得的成就和最新世界经济、政治时事的了解.组织者按班级将参赛人员随机分为若干组,每组均为两名选手,每组对抗赛开始时,组织者随机从准备好的题目中抽取2道试题供两位选手抢答,每位选手抢到每道试题的机会相等.比赛得分规则为:选手抢到试题且回答正确得10分,对方选手得0分;选手抢到试题但回答错误或没有回答得0分,对方选手得5分;2道题目抢答完毕后得分多者获胜.已知甲、乙两名选手被分在同一组进行对抗赛,每道试题甲回答正确的概率为 , 乙回答正确的概率为 , 两名选手回答每道试题是否正确相互独立.2道试题抢答后的各自得分作为两位选手的个人总得分.(1)、求乙总得分为10分的概率;(2)、记X为甲的总得分,求X的分布列和数学期望.