广东省深圳市2023年南外、南二外初三数学一模试卷
试卷更新日期：2023-04-20 类型：中考模拟
一、单选题(每小题3分，共30分)
-
1. 在1，－2，0，这四个数中，最大的数是（ ）A、1 B、－2 C、0 D、2. 下列运算正确的是（ ）A、a3+a2=a5 B、=5 C、(a+b)2=a2+b2 D、a6÷a3=a23. 地球上的陆地面积约为149000000km2 ， 数字14000000用科学记数法表示为（ ）A、1.49×107 B、1.49×108 C、1.49×109 D、1.49×10104. “成语”是中华文化的瑰宝，是中华文化的微缩景观.下列成语：①“水中捞月”，②“守株待兔”，③“百步穿杨”，④“瓮中捉鳖”描述的事件是不可能事件的是（ ）A、① B、② C、③ D、④5. 图2是图1中长方体的三视图，用S表示面积，S主=x2+3x，S左=x2+x，则S俯=（ ）
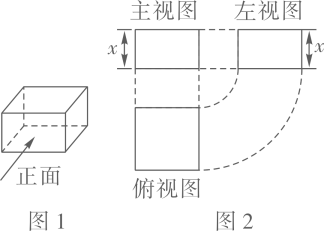A、x2+3x +2 B、x2+2x+1 C、x2+4x+3 D、2x2+4x6. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术，其中方程术是其最高的代数成就．《九章算术》中有这样一个问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”译文：“相同时间内，走路快的人走100步，走路慢的人只走60步．若走路慢的人先走100步，走路快的人要走多少步才能追上？(注：步为长度单位)”设走路快的人要走x步才能追上，根据题意可列出的方程（ ）60
A、x=100-x B、x=100+x C、x=100+x D、x=100-x7. 五名同学捐款数分别是5，3，6，5，10（单位：元），捐10元的同学后来又追加了10元．追加后的5个数据与之前的5个数据相比，集中趋势相同的是（）A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数8. 小王同学从家出发，步行到离家a米的公园晨练，4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练，爸爸到达公园后立即以原速折返回到家中，两人离家的距离y（单位：米）与出发时间x（单位：分钟）的函数关系如图所示，则两人先后两次相遇的时间间隔为（ ）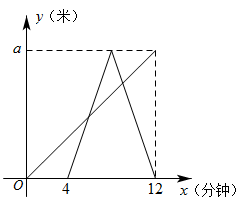
A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟9. 如图，AB是⊙O的直径，将弦AC绕点A顺时针旋转30°得到AD，此时点C的对应点D落在AB上，延长CD，交⊙O于点E，若CE=4，则图中阴影部分的面积为（ ）
A、2π B、 C、2π-4 D、2π-10. 如图，四边形ABCD是边长为4的菱形，对角线AC，BD的长度分别是一元二次方程x2-mx-x+2m=0的两实数根，DH是AB边上的高，则DH值为（ ）
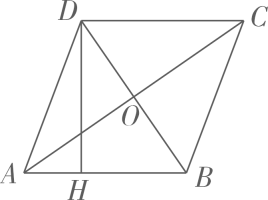A、 B、 C、 D、3二、填空题(每小题3分，共15分)
-
11. 因式分解： 2x3-4x2+2x=12. 幻方，最早源于我国，古人称之为纵横图．如图所示的幻方中，各行、各列及各条对角线上的三个数字之和均相等，则图中a的值为
-1 -6 1 0 a -4 -5 2 -3 13. 如图，在建高铁的某段路基横断面为梯形ABCD，DC∥AB．BC长6米，坡角β为45°，AD的坡角α为30°，则AD长为米 (结果保留根号)．
14. 如图，一次函数y=2x与反比例函数y=(k>0)的图象交于A，B两点，点M在以C(4，0)为圆心，半径为2的 ⊙ C上，N是BM的中点，已知ON长的最大值为3，则k的值是
15. 如图，在Rt△ABC中，∠BAC= =90°，AB= ， AC=6，点E在线段AC上，且AE=1，D是线段BC上的一点，连接DE，将四边形ABDE沿直线DE翻折，得到四边形FGDE，当点G恰好落在线段AC上时，AF=
三、解答题(共55分)
-
16. 计算：(π-1)0+4sin45°-+|-3|．17. 解不等式组 ． 请按下列步骤完成解答．(1)、解不等式①，得；(2)、解不等式②，得；(3)、把不等式①和②的解集在数轴上表示出来：
(4)、原不等式组的解集是。18. 某校为落实“双减”工作，增强课后服务的吸引力，充分用好课后服务时间，为学有余力的学生拓展学习空间，成立了5个活动小组(每位学生只能参加一个活动小组)： A．音乐：B．体育：C．美术；D．阅读；E．人工智能．为了解学生对以上活动的参与情况，随机抽取部分学生进行了调查统计，并根据统计结果，绘制了如图所示的两幅不完整的统计图．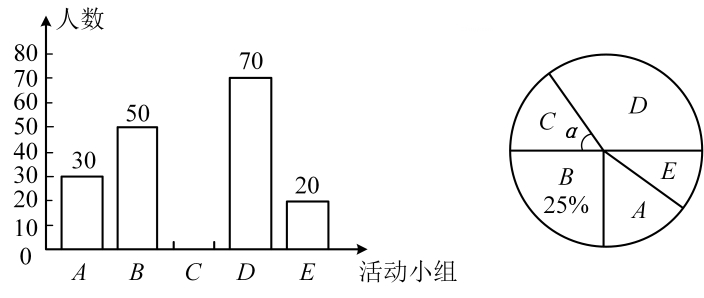
根据图中信息，解答下列问题：
(1)、①此次调查一共随机抽取了 ▲ 名学生；②补全条形统计图(要求在条形图上方注明人数)；
③扇形统计图中圆心角α= ▲ 度；
(2)、若该校有3200名学生，估计该校参加D组(阅读)的学生人数；(3)、刘老师计划从E组(人工智能)的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛，请用树状图法或列表法求出恰好抽中甲、乙两人的概率．解： (1)①200解析： 50÷25%= 200．
③360°×=54°．
19. 如图，BD是矩形ABCD的对角线.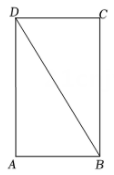
(1)、求作⊙A，使得⊙A与BD相切（要求：尺规作图，不写作法，保留作图痕迹）；(2)、在（1）的条件下，设BD与⊙A相切于点E，CF⊥BD，垂足为F.若直线CF与⊙A相切于点G，求的值.20. 某公司电商平台，举行了商品打折促销活动，经市场调查发现，某种商品的周销售量y(件)是关于售价x(元/件)的一次函数，下表仅给出了该商品售价x，周销售量y，周销售利润W(元)的三组对应值数据：x
40
70
90
y
180
90
30
W
3600
4500
2100
(注：周销售利润=周销售量×(售价-进价))
(1)、求y关于x的函数解析式(不要求写出自变量的取值范围)；(2)、若该商品进价为a(元/件)，售价x为多少时，周销售利润W最大？并求出此时的最大利润；(3)、因疫情原因，该商品进价提高了m(元/件) (m>0)，公司为回馈消费者，规定该商品售价x不得超过55(元/件)，且该商品在今后的销售中，周销售量与售价仍然满足(1)中的函数关系，若周销售最大利润是4050元，求m的值．21. 如图1，在等腰三角形ABC中，∠A=90°，AB=AC，点D、E分别在边AB，AC上，AD=AE，连接BE，点M，N，P分别为DE，BE，BC的中点．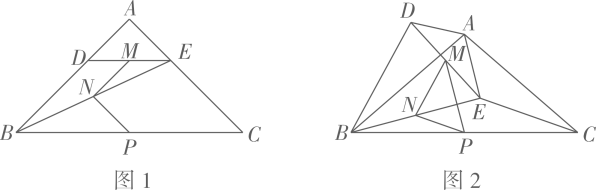
(1)、观察猜想：图1中，线段MN与NP的数量关系是 ， ∠MNP的大小是；
(2)、探究证明：把△ADE绕点A顺时针方向旋转到图2的位置，连接MP、BD、CE，判断△MNP的形状，试说明理由；
(3)、拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=1，AB=3，请直接写出△MNP面积的最大值．
22. 已知一次函数y=kx+b(k≠0)的图像与二次函数y=(x+2)2-2的图像相交于点A(1，m)，B(-2，n)．
(1)、求一次函数的表达式，并在图中画出这个一次函数的图象；(2)、根据函数图象，直接写出不等式kx+b<(x+2)2-2的解集；(3)、当-3≤x≤1时，直线y=(x+2)2-2与直线y=n只有一个交点，求n的取值范围．(4)、把二次函数y=(x+2)2-2的图像左右平移得到抛物线G：y=(x-m)2-2，直接写出当抛物线G与线段AB只有一个交点时m的取值范围。