山西省晋中市平遥县2022-2023学年七年级下学期3月月考数学试卷

试卷更新日期：2023-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 某种病毒近似于球体，它的半径约为0.000000005米，用科学记数法表示为（）

A、5×10⁸ B、5×10⁹ C、5×10^﹣8 D、5×10^﹣9

查看试题解析
2. 已知 $a^{m} = 3 ， a^{n} = 2$ ，那么 $a^{m + n + 2} =$ （）

A、8 B、7 C、 $6 a^{2}$ D、 $6 + a^{2}$

查看试题解析
3. 计算 ${(a + b)}^{2}$ 的正确结果是（）.

A、 $a^{2} + b^{2}$ B、 $a^{2} - b^{2}$ C、 $a^{2} + b^{2} + 2 a b$ D、 $a^{2} - 2 a b + b^{2}$

查看试题解析
4. 下列运算正确的是（　）

A、b⁵÷b³＝b² B、（b⁵）³＝b⁸ C、b³b⁴＝b¹² D、a（a-2b）＝a²+2ab

查看试题解析
5. 下列代数式中能用平方差公式计算的是（）

A、 $(x + y) (x + y)$ B、 $(2 x - y) (y + 2 x)$ C、 $(x + \frac{1}{2} y) (y - \frac{1}{2} x)$ D、 $(- x + y) (y - x)$

查看试题解析
6. 已知 $x = 3 y + 5$ ，且 $y (3 y + 5) = 1$ ，则 $x y (x - 3 y)$ 的值为（）

A、0 B、1 C、5 D、12

查看试题解析
7. 某商场四月份售出某品牌衬衣b件，每件c元，营业额a元．五月份采取促销活动，售出该品牌衬衣3b件，每件打八折，则五月份该品牌衬衣的营业额比四月份增加（　　）

A、1.4a元 B、2.4a元 C、3.4a元 D、4.4a元

查看试题解析
8. 若长方形的面积是4a²+8ab+2a，它的一边长为2a，则它的周长为（）

A、2a+4b+1 B、2a+4b C、4a+4b+1 D、8a+8b+2

查看试题解析
9. “数形结合”思想是一种常用的数学思想，其中“以形助数”是借助图形来理解和记忆数学公式．如图所示，将四张全等的长方形硬纸片围成一个正方形，根据图形面积的关系，可以直观地得到一个关于a、b的恒等式为（）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = (a + b)^{2} - 4 a b$ D、 $a^{2} + a b = a (a + b)$

查看试题解析
10. 观察下列各式及其展开式
${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$
${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$
${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$
${(a + b)}^{5} = a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}$ ……
请你猜想 ${(2 x - 1)}^{10}$ 的展开式中含 $x^{2}$ 项的系数是（）

A、144 B、180 C、220 D、45

查看试题解析

二、填空题

11. 计算： $10 x^{3} y^{2} \div 5 x^{3} y =$ ．

查看试题解析
12. 若多项式 $4 a^{2} + k a + 16$ 是一个完全平方式，则k= ．

查看试题解析
13. 已知 $2 a + 4 b - 4 = 0$ ，则 $9^{a} \times 8 1^{b} =$ ．

查看试题解析
14. 如图，从边长为 $(a + 4) c m$ 的正方形纸片中剪去一个边长为 $(a + 1) cm$ 的正方形 $(a > 0)$ ，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的周长为 $cm$ ．

查看试题解析
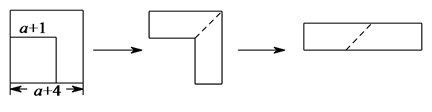15. 如图是一段T形钢材示意图，根据图中给出的尺寸，可计算其体积为．（用含a的代数式表示）

查看试题解析

三、解答题

16. 计算

(1)、 $4^{3} \times 6 \times 2 5^{3}$ ；

(2)、 ${(- \frac{1}{3})}^{- 2} + (- 1)^{2019} - | - 2^{3} | + (π - 5)^{0}$ ．

查看试题解析
17.

(1)、化简： $(3 x^{2} y^{2} + 4 x^{3} y - 4 x^{2} y) \div x y - (2 x - 1)^{2}$ ．

(2)、先化简，再求值： $(2 x + y)^{2} - 4 x (x + 2 y) - 3 y^{2}$ ，其中 $x = - 4$ ， $y = \frac{1}{2}$ ．

查看试题解析
18. 一堂习题课上，数学老师在黑板上出了这样一道题：当 $a = 2014 ， b = 2$ 时，求 $[3 a^{2} b (b - a) + a (3 a^{2} b - a b^{2})] \div a^{2} b$ 的值．一会儿，雯雯说“老师，您给的‘ $a = 2014$ ’这个条件是多余的．”一旁的小明反驳道：“题目中有两个字母，不给这个条件，肯定求不出结果！”他们谁说得有道理？请说明理由．

查看试题解析
19. 世界上最小、最轻的昆虫是膜翅目缨小蜂科的一种卵蜂，体长仅0.021厘米，其质量也只有0.000005克．

(1)、用科学记数法表示上述两个数据．

(2)、一个鸡蛋的质量大约是50克，多少只卵蜂的质量和与这个鸡蛋的质量相等？

查看试题解析
20. 公元3世纪，古希腊数学家丢番图（Diophantus）在其《算术》一书中设置了以下问题：已知两正整数之和为20，乘积为96，求这两个数．因为两数之和为20，所以这两个数不可能同时大于10，也不可能同时小于10，必定是一个大于10，一个小于10．根据如图所示的设法，可设一个数为 $10 + x$ ，则另一个数为 $10 - x$ ，根据两数之积为96，可得 $(10 + x) (10 - x) = 96$ ．请根据以上思路解决下列问题：

(1)、若两个正整数之和为100，大数比小数大 $2 a$ ，根据丢番图的设法，这两个正整数可表示为和；

(2)、请你根据丢番图的运算方法，计算 $502 \times 498$ 的值．

查看试题解析
21. 眉山市三苏雕像广场是为了纪念三苏父子而修建的．原是一块长为(4a+2b)米，宽为(3a-b)米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为（a+b）米的正方形三苏父子雕像，则绿化的面积是多少平方米？并求出当a=20，b=10时的绿化面积．

查看试题解析
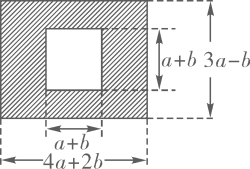22. 学习了《整式的乘除》这一章之后，小明联想到小学除法运算时，会碰到余数的问题，那么类比多项式除法也会出现余式的问题．例如，如果一个多项式（设该多项式为A）除以 $2 x^{2}$ 的商为 $3 x + 4$ ，余式为 $x - 1$ ，那么这个多项式是多少？他通过类比小学除法的运算法则：被除数=除数×商+余数，推理出多项式除法法则：被除式=除式×商+余式．
请根据以上材料，解决下列问题：

(1)、请你帮小明求出多项式；

(2)、小明继续探索，如果一个多项式除以 $2 x - 6$ 商为 $3 x - 1$ ，余式为 $x + 3$ ，请你根据以上法则求出该多项式；

(3)、上述过程中，小明把小学的除法运算法则运用在多项式除法运算上，这里运用的数学思想是____．

A、类比思想 B、公理化思想 C、函数思想 D、数形结合思想

查看试题解析
23. 综合与实践

图1是一个长为a，宽为b的长方形．现有相同的长方形若干，进行如下操作：

(1)、用四块图1的小长方形不重叠地拼成一个如图2所示的正方形．请利用图2中阴影部分面积的不同表示方法，直接写出代数式 $(a + b)^{2}$ ， $(a - b)^{2}$ ， $a b$ 之间的等量关系；

(2)、将六块图1的小长方形不重叠地拼成一个如图3所示的长方形，通过不同方法计算阴影部分的面积，你能得到什么等式？请写出你的结论并用乘法法则证明这个等式成立；

(3)、现有图1的小长方形若干个，图4边长为a的正方形两个，边长为b的正方形两个请你用这些图形拼成一个长方形（不重叠），使其面积为 $2 a^{2} + 5 a b + 2 b^{2}$ ．画出你所拼成的长方形，并写出长方形的长和宽分别为多少．

查看试题解析