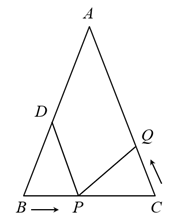山东省枣庄市薛城区五校联考2022-2023学年七年级下学期3月月考数学试题
试卷更新日期：2023-04-20 类型：月考试卷
一、单选题
-
1. 下列世界博览会会徽图案中是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列长度的三条线段能组成三角形的是（ ）A、5cm 2cm 3cm B、5cm 2cm 2cm C、5cm 2cm 4cm D、5cm 12cm 6cm3. 某同学把三角形的玻璃打碎成了3块，现要到玻璃店配一块完全一样的玻璃，那么最省事方法是（ ）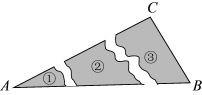
A、带①去 B、带②去 C、带③去 D、①②③都带去4. 不能判定两个三角形全等的条件是（ ）A、三条边对应相等 B、两角及一边对应相等 C、两边及夹角对应相等 D、两边及一边的对角相等5. 如图，∠1＝∠2，要说明△ABD≌△ACD，需从下列条件中选一个，错误的选法是（ ）
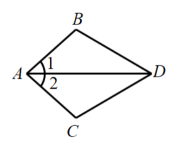A、∠ADB＝∠ADC B、∠B＝∠C C、DB＝DC D、AB＝AC6. 直角三角形的一个锐角∠A是另一个锐角∠B的3倍，那么∠B的度数是（ ）A、22.5° B、45° C、67.5° D、135°7. 某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计)，其中凳腿AB和CD的长相等，O是它们的中点.为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为30 cm，则由以上信息可推得CB的长度也为30 cm，依据是（ ）
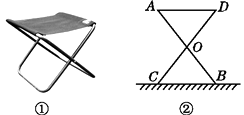A、SAS B、ASA C、SSS D、AAS8. 如图，在△ABC中，AB＝AC，AD⊥BC，∠B＝30°，则∠CAD的度数为（ ）
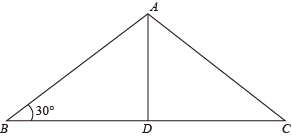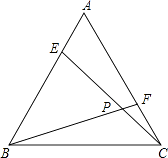
A、30° B、60° C、90° D、120°9. 如图，DE是线段AB垂直平分线．AC＝5cm，△ADC的周长为17cm，则BC的长为（ ）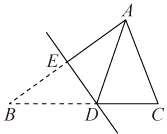
A、7cm B、10cm C、12cm D、22cm10. 如果等腰三角形两边长是6和3，那么它的周长是( ）A、15或12 B、9 C、12 D、1511. 如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E=35°，则∠BAC的度数为（ ）
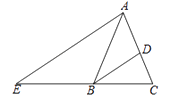A、40° B、45° C、50° D、55°12. 如图，点D为△ABC边AB的中点，将△ABC沿经过点D的直线折叠，使点A刚好落在BC边上的点F处，若∠B=46°，则∠BDF的度数为（ ）
A、88° B、86° C、84° D、82°二、填空题
-
13. 超重机的底座、输电线路的支架、自行车的斜支架等，都是采用三角形结构，这样做的数学道理是利用了 ．14. △ABC中，当时，这个三角形是三角形．（填“锐角”“直角”或“钝角”）15. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F．若 ， DE＝4，AB＝8，则AC长是 ．
16. 在△ABC中，∠A=80°，∠ABC与∠ACB的平分线交于点O，则∠BOC=度．
17. 将一副直角三角尺按如图所示摆放，则图中 的度数是.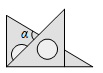
18. 如图，和都是等边三角形，A、B、D三点共线．下列结论：①；②；③平分；④ ， ⑤是等边三角形．其中正确的有（只填序号）．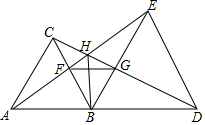
三、解答题
-
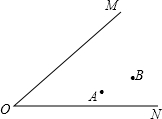
19. 一犯罪分子正在两交叉公路间沿到两公路距离相等的一条小路上逃跑，埋伏在A、B两处的两名公安人员想在距A、B相等的距离处同时抓住这一罪犯.请你帮助公安人员在图中设计出抓捕点.
20. 如图，在△ABC中，AD是高，BE是角平分线，AD、BE交于点F，∠C=30°，∠BFD=70°，求∠BAC的度数．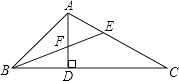
21. 如图，在所给正方形每个小网格的边长是1的图中完成下列各题．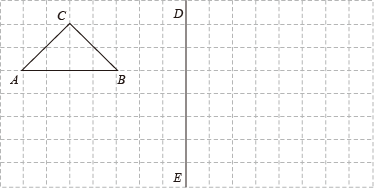
( 1 )△ABC的面积是 ；
( 2 )画出格点△ABC关于直线DE对称的；
( 3 )在DE上画出点Q，使QA＋QC最小．
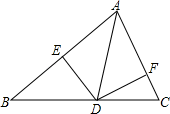
22. 如图，D、E、F、B在一条直线上，AB=CD，∠B=∠D，BF=DE，求证：AECF．
