山东省济宁市金乡县2022-2023学年七年级下学期3月月考数学试题
试卷更新日期:2023-04-20 类型:月考试卷
一、单选题
-
1. 如图,下列说法错误的是( )
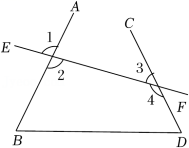 A、∠1与∠2是对顶角 B、∠1与∠3是同位角 C、∠1与∠4是内错角 D、∠B与∠D是同旁内角2. 若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )A、50° B、130° C、50°或130° D、无法确定3. 如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )A、相等 B、互余或互补 C、互补 D、相等或互补4. 直线a,b,c,在同一平面内,下列种说法中,正确的个数为( )
A、∠1与∠2是对顶角 B、∠1与∠3是同位角 C、∠1与∠4是内错角 D、∠B与∠D是同旁内角2. 若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )A、50° B、130° C、50°或130° D、无法确定3. 如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )A、相等 B、互余或互补 C、互补 D、相等或互补4. 直线a,b,c,在同一平面内,下列种说法中,正确的个数为( )①如果 , , 那么;
②如果 , , 那么;
③如果 , , 那么;
④如果a与b相交,b与c相交,那么a与c相交.
A、1 B、2 C、3 D、45. 下列命中,真命题是( )A、相等的两个角是对顶角 B、如果两条直线被第三条直线所截,那么同位角相等 C、从直线外一点到这条直线的垂线段叫做该点到直线的距离 D、在同一平面内,过一点有且只有一条直线与已知直线垂直6. 如图,在中,点D,E,F分别在边 , , 上,下列不能判定的条件是( )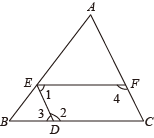 A、 B、 C、 D、7. 下列现象是平移的是( )A、电梯从底楼升到顶楼 B、卫星绕地球运动 C、纸张沿着它的中线对折 D、树叶从树上落下8. 如图所示, , , 下列说法错误的是( )
A、 B、 C、 D、7. 下列现象是平移的是( )A、电梯从底楼升到顶楼 B、卫星绕地球运动 C、纸张沿着它的中线对折 D、树叶从树上落下8. 如图所示, , , 下列说法错误的是( ) A、点B到AC的垂线段是线段AB B、点C到AB的垂线段是线段AC C、线段AD是点D到BC的垂线段 D、线段BD是点B到AD的垂线段9. 如图, , , 探索图中角α,β,γ之间的关系式正确的是( )
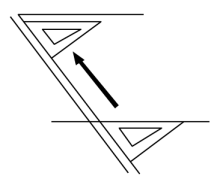
A、点B到AC的垂线段是线段AB B、点C到AB的垂线段是线段AC C、线段AD是点D到BC的垂线段 D、线段BD是点B到AD的垂线段9. 如图, , , 探索图中角α,β,γ之间的关系式正确的是( ) A、 B、 C、 D、10. 一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( )
A、 B、 C、 D、10. 一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( ) A、纸带①的边线平行,纸带②的边线不平行 B、纸带①、②的边线都平行 C、纸带①的边线不平行,纸带②的边线平行 D、纸带①、②的边线都不平行
A、纸带①的边线平行,纸带②的边线不平行 B、纸带①、②的边线都平行 C、纸带①的边线不平行,纸带②的边线平行 D、纸带①、②的边线都不平行二、填空题
-
11. 如图,给出了直线外一点作已知直线平行线的一种方法,它的依据是。
 12. 把“同角的余角相等”改成“如果…,那么…”:.13. 如图: , , 垂足分别为A、D,则图中线段的长度能表示点到直线的距离的共有条.
12. 把“同角的余角相等”改成“如果…,那么…”:.13. 如图: , , 垂足分别为A、D,则图中线段的长度能表示点到直线的距离的共有条.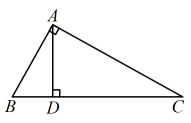 14. 一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;n条直线两两相交,最多有个交点.15. 金乡县某中学七年级共有四个班,每班各选5名同学组成一个代表队,这四支代表队(分别用A,B,C,D表示)进行数学知识应用竞赛,前三名将参加金乡县数学知识竞赛,甲,乙,丙三位同学预测的结果分别为:甲:C得亚军;D得季军;乙:D得冠军;A得亚军;丙:C得冠军;B得亚军.已知每人的预测都是半句正确,半句错误,则冠,亚,季,殿军分别为 .
14. 一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;n条直线两两相交,最多有个交点.15. 金乡县某中学七年级共有四个班,每班各选5名同学组成一个代表队,这四支代表队(分别用A,B,C,D表示)进行数学知识应用竞赛,前三名将参加金乡县数学知识竞赛,甲,乙,丙三位同学预测的结果分别为:甲:C得亚军;D得季军;乙:D得冠军;A得亚军;丙:C得冠军;B得亚军.已知每人的预测都是半句正确,半句错误,则冠,亚,季,殿军分别为 .三、解答题
-
16. 如图,现有以下3个论断:①ABCD;②∠B=∠C;③∠E=∠F.请以其中2个论断为条件,另一个论断为结论构造命题.
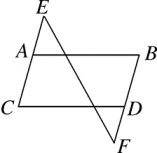 (1)、你构造的是哪几个命题?(2)、请选择其中一个真命题加以证明.17. 完成下面的证明.
(1)、你构造的是哪几个命题?(2)、请选择其中一个真命题加以证明.17. 完成下面的证明.如图、与互补, , 求证:.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
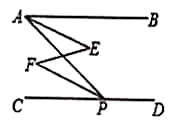
证明:与互补,(已知)
.( )
.( )
, (已知)
, (等量代换)
即_▲_=_▲_.
.( )
.( )
18. 已知:如图,直线相交于点O,平分 , . (1)、的对顶角是;的邻补角是 .(2)、求的度数.19. 如图,在的正方形网格中有 , 点均在格点上.
(1)、的对顶角是;的邻补角是 .(2)、求的度数.19. 如图,在的正方形网格中有 , 点均在格点上.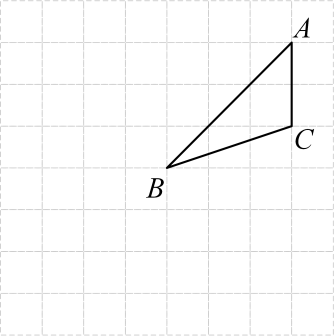 (1)、画出点B到直线的最短路径;(2)、过C点画出的平行线,交于点E;(3)、将向左平移格,再向下平移格后得到 , 画出 .(4)、判断和的数量关系 .20. 如图, , 与交于点O,平分 , .
(1)、画出点B到直线的最短路径;(2)、过C点画出的平行线,交于点E;(3)、将向左平移格,再向下平移格后得到 , 画出 .(4)、判断和的数量关系 .20. 如图, , 与交于点O,平分 , .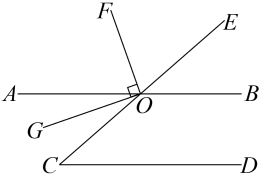 (1)、若 , 求的度数;(2)、求证:平分 .21. 已知直线 , 直线分别交、于点A、C,是的平分线,交于点H,过点A作交于点G.
(1)、若 , 求的度数;(2)、求证:平分 .21. 已知直线 , 直线分别交、于点A、C,是的平分线,交于点H,过点A作交于点G.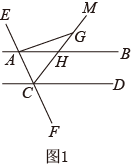
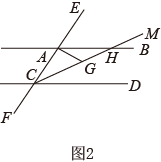 (1)、如图1,点G在的延长线上时,若 , 求的度数;(2)、如图2,点G在上时,试说明: .22. 已知AB∥CD,线段EF分别与AB、CD相交于点E、F.
(1)、如图1,点G在的延长线上时,若 , 求的度数;(2)、如图2,点G在上时,试说明: .22. 已知AB∥CD,线段EF分别与AB、CD相交于点E、F.

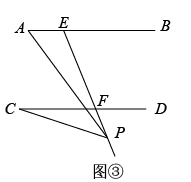 (1)、如图①,当∠A=20°,∠APC=70°时,求∠C的度数;(2)、如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量关系?试证明你的结论;(3)、如图③,当点P在线段EF的延长线上运动时,(2)中的结论还成立吗?如果成立,请说明理由;如果不成立,试探究它们之间新的数量关系并证明.
(1)、如图①,当∠A=20°,∠APC=70°时,求∠C的度数;(2)、如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量关系?试证明你的结论;(3)、如图③,当点P在线段EF的延长线上运动时,(2)中的结论还成立吗?如果成立,请说明理由;如果不成立,试探究它们之间新的数量关系并证明.