广东省惠州市惠阳区十校联考2021-2022学年七年级下学期数学试卷
试卷更新日期:2023-04-20 类型:月考试卷
一、单选题
-
1. 等于( )A、-2022 B、 C、 D、20222. 环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为( )
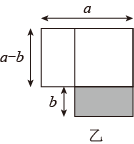
A、2.5×105 B、2.5×106 C、2.5×10﹣5 D、2.5×10﹣63. 将2个红球、3个白球、2个黑球放入一个不透明袋子里,从中摸出6个球,恰好红球、白球、黑球都摸到,这个事件是( )A、不太可能件 B、不可能事件 C、随机事件 D、必然事件4. 一副直角三角板如下图放置( , , ),如果点C在的延长线上,点B在上,且 , 则的度数为( )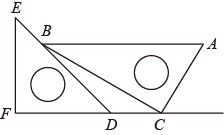 A、10° B、15° C、18° D、30°5. 将图甲中明影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于a、b的恒等式为( )
A、10° B、15° C、18° D、30°5. 将图甲中明影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于a、b的恒等式为( )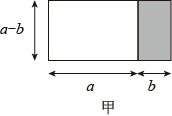
 A、 B、 C、 D、6. 观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是( )
A、 B、 C、 D、6. 观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是( ) A、10 B、14 C、21 D、157. 下列说法中正确的是( )A、两条直线被第三条直线所截,内错角相等; B、在同一平面内,垂直于同一条直线的两条直线平行; C、直线外一点到这条直线的垂线段叫做点到直线的距离; D、在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系.8. 小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离s与时间t的关系示意图是( )A、
A、10 B、14 C、21 D、157. 下列说法中正确的是( )A、两条直线被第三条直线所截,内错角相等; B、在同一平面内,垂直于同一条直线的两条直线平行; C、直线外一点到这条直线的垂线段叫做点到直线的距离; D、在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系.8. 小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离s与时间t的关系示意图是( )A、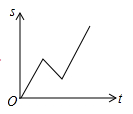 B、
B、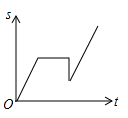 C、
C、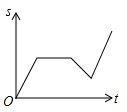 D、
D、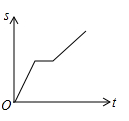 9. 某车间的甲、乙两名工人分别同时开始生产同种零件,他们一天生产零件y(个)与生产时间的关系如图所示,下列说法正确的有( )
9. 某车间的甲、乙两名工人分别同时开始生产同种零件,他们一天生产零件y(个)与生产时间的关系如图所示,下列说法正确的有( )①乙一天的生产任务比甲一天的生产任务多
②甲先完成任务
③工人甲因机器故障停止生产了 , 修好机器后生产速度是每小时15个
④在工作 , 时甲、乙两名工人生产零件个数相等
 A、1个 B、2个 C、3个 D、4个10. 如图,两个正方形边长分别为a、b,如果 , , 则阴影部分的面积为( )
A、1个 B、2个 C、3个 D、4个10. 如图,两个正方形边长分别为a、b,如果 , , 则阴影部分的面积为( )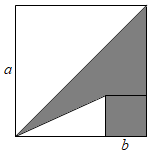 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:a(a-3)= .12. 如果关于 的多项式 是一个完全平方式,那么13. 比较大小: (填“>”、“<”或“=”).14. 小明将飞镖随意投中如图所示的正方体木框中,那么投中阴影部分的概率为 .
 15. 观察等式: , , ,……,已知按一定规律排列的一组数: , , ,……, ,若 ,用含 的代数式表示这组数的和是.
15. 观察等式: , , ,……,已知按一定规律排列的一组数: , , ,……, ,若 ,用含 的代数式表示这组数的和是.三、解答题
-
16. 计算:(1)、;(2)、 . (要求简便计算)17. 化简求值: , 其中 , .18. 某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图的统计图.请根据相关信息,解答下列问题:
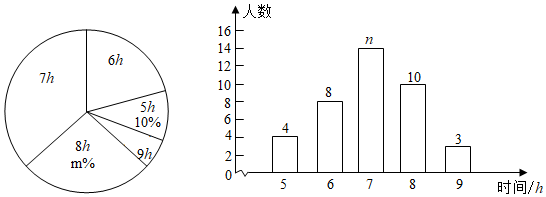 (1)、扇形统计图中的m= , 条形统计图中的n=;(2)、从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是;(3)、若该校共有1600名学生,则根据样本数据,估计该校初中学生每天睡眠时间少于8小时的人数.19. 如图,点D、E、F、G均在的边上,连接BD、DE、FG,∠3=∠CBA,FG//BD.
(1)、扇形统计图中的m= , 条形统计图中的n=;(2)、从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是;(3)、若该校共有1600名学生,则根据样本数据,估计该校初中学生每天睡眠时间少于8小时的人数.19. 如图,点D、E、F、G均在的边上,连接BD、DE、FG,∠3=∠CBA,FG//BD. (1)、求证:∠1+∠2=180°;(2)、若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.20. 如图,点C,D在直线上, , .
(1)、求证:∠1+∠2=180°;(2)、若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.20. 如图,点C,D在直线上, , .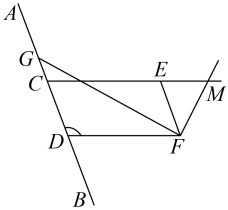 (1)、求证:
(1)、求证:∵(已知)
又∵_▲_
∴_▲_( )
∴( )
(2)、的角平分线交于点O,过点F作交的延长线于点M.若 , 再求的度数.21. 阅读:若x满足 , 求的值.解:设 , 则 ,
所以 .
请仿照上例解决下面的问题:
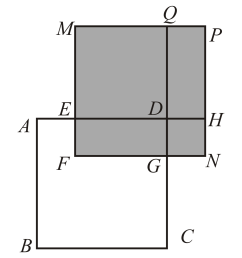 (1)、若x满足 , 求的值;(2)、若x满足 , 求的值;(3)、如图,正方形的边长为 , 长方形的面积是500,四边形和都是正方形,四边形是长方形,求图中阴影部分的面积(结果必须是一个具体数值).22. 如图是甲骑自行车与乙骑摩托车分别从A,B两地向C地(A,B,C地在同一直线上)行驶过程中离B地的距离与行驶时间的关系图,请你根据图象回答下列问题:
(1)、若x满足 , 求的值;(2)、若x满足 , 求的值;(3)、如图,正方形的边长为 , 长方形的面积是500,四边形和都是正方形,四边形是长方形,求图中阴影部分的面积(结果必须是一个具体数值).22. 如图是甲骑自行车与乙骑摩托车分别从A,B两地向C地(A,B,C地在同一直线上)行驶过程中离B地的距离与行驶时间的关系图,请你根据图象回答下列问题: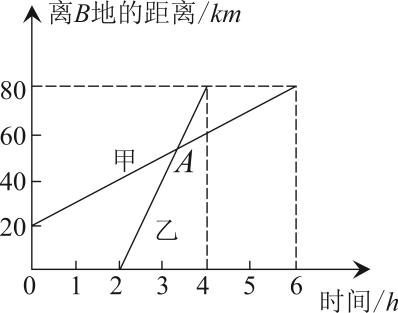 (1)、A点表示的意义是什么?(2)、甲、乙两人在途中行驶的平均速度分别为多少?(3)、直接写出甲乙两人相距时t的值.
(1)、A点表示的意义是什么?(2)、甲、乙两人在途中行驶的平均速度分别为多少?(3)、直接写出甲乙两人相距时t的值.