山西省忻州市代县2022-2023学年八年级下学期段考数学试卷（一）

试卷更新日期：2023-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知实数a在数轴上的位置如图所示，则化简： $| a - 2 | + \sqrt{{(a - 4)}^{2}}$ 的结果为（）

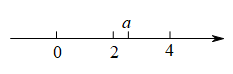A、2 B、-2 C、2a-6 D、-2a+6

查看试题解析
2. 化简 $\sqrt{\frac{1}{2}}$ 的结果是（）

A、1 B、 $\sqrt{2}$ C、2 D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 下列计算中，正确的是（）

A、 $\sqrt[3]{{(- 2)}^{2}} = - 2$ B、 $5 \sqrt{2} - \sqrt{2} = 5$ C、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
4. 已知一个直角三角形的两条边的长分别为3和4，则它的第三条边是（）

A、5或 $\sqrt{7}$ B、 $\sqrt{7}$ C、5 D、2或5

查看试题解析
5. 若 $△ A B C$ 的三边a、b、c，满足 $(a - b) (a^{2} + b^{2} - c^{2}) = 0$ ，则 $△ A B C$ 是（）

A、等腰三角形 B、直角三角形 C、等腰三角形或直角三角形 D、等腰直角三角形

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，垂足为D．若 $A C = 3$ ， $B C = 4$ ，则 $C D$ 的长为（）

A、2.4 B、2.5 C、4.8 D、5

查看试题解析
7. 在△ABC中， $A B = 15 ， A C = 13$ ， $B C$ 边上的高 $A D = 12$ ，则边 $B C$ 的长为（）

A、4 B、14 C、4 或14 D、8或14

查看试题解析
8. 设a= $\sqrt{2}$ ， b= $\sqrt{3}$ ，用含a，b的式子表示 $\sqrt{2.16}$ ，则下列表示正确的是（　　）

A、 $0.3 a b$ B、 $0.6 a b$ C、2ab D、 $2 a^{2} b$

查看试题解析
9. 如图所示， $C D = 1 ， ∠ B C D = 90 °$ ，若数轴上点A所表示的数为a，则a的值为（　　）

A、 $- \sqrt{5}$ B、 $1 - \sqrt{5}$ C、 $- 1 - \sqrt{5}$ D、 $- 1 + \sqrt{5}$

查看试题解析
10. 如图，△ABD和△CBD，∠ADB=90°，∠ABD=∠DBC，AD=DC=1，若AB=4，则BC的长为（）

A、 $\frac{5}{2}$ B、2 $\sqrt{2}$ C、3 D、 $\frac{7}{2}$

查看试题解析

二、填空题

11. 计算： ${(\sqrt{3} + \sqrt{2})}^{2023} \cdot {(\sqrt{3} - \sqrt{2})}^{2022} =$ ．

查看试题解析
12. 一个无盖的长方体盒子的长、宽、高分别 $4 c m ， 4 c m ， 6 c m$ ，一只蚂蚁想从盒底的点A爬到盒顶的点B，蚂蚁要爬行的最短路程为 $c m$ ．

查看试题解析
13. 若 $\sqrt{20 n}$ 是整数，则正整数n的最小值为．

查看试题解析
14. 到目前为止，勾股定理的证明已超过 $400$ 种，其中一种简洁易懂方法叫做“常春证法”，两个直角三角形如图摆放，已知 $R t Δ A B C ≌ R t Δ D E F$ ，点F落在 $A C$ 上，点C与点E重合，斜边 $A B$ 与斜边 $C D$ 交于点M，连接 $A D$ ， $B D$ ，若 $A C ＝ 9$ ， $B C ＝ 5$ ，则四边形 $A B C D$ 的面积为．

查看试题解析
15. 将一列数 $\sqrt{2}$ ， 2， $\sqrt{6}$ ， 2 $\sqrt{2}$ ， $\sqrt{10}$ ， …，10 $\sqrt{2}$ 按如图的数表排列，按照该方法进行排列，3 $\sqrt{2}$ 的位置可记为（2，4），2 $\sqrt{6}$ 的位置可记为（3，2），那么这列数中的最大有理数按此排法的位置可记为（m，n），则m+n的值为．
$\sqrt{2}$     2        $\sqrt{6}$          $2 \sqrt{2}$           $\sqrt{10}$
$2 \sqrt{3}$    $\sqrt{14}$       4           $3 \sqrt{2}$           $2 \sqrt{5}$
$\sqrt{22}$     $2 \sqrt{6}$       ···           ···             ···
·                                                             ·
·                                                             ·
·                                                           ·
···    ···         ···           ···     $10 \sqrt{2}$

查看试题解析

三、解答题

16. 计算：

(1)、 $2 \sqrt{8} + \frac{1}{3} \sqrt{18} - \frac{3}{4} \sqrt{32}$ ；

(2)、 $2 (\sqrt{48} - 4 \sqrt{\frac{1}{8}}) - (3 \sqrt{\frac{1}{3}} - 2 \sqrt{0.5})$ ；

(3)、 $\sqrt{50} \times \sqrt{8} - \frac{\sqrt{6} \times \sqrt{3}}{\sqrt{2}}$ ；

(4)、 $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) - {(\sqrt{5} - 1)}^{2}$ ．

查看试题解析
17. 如图，有一块直角三角形纸片，两直角边 $A C = 6 c m$ ， $B C = 8 c m$ ，现将直角边 $A C$ 沿直线 $A D$ 折叠，使点C落在斜边 $A B$ 上的点E处，试求 $C D$ 的长．

查看试题解析
18. 如图，学校操场边上一块空地（阴影部分）需要绿化，连接 $A C$ ，测出 $C D ＝ 3$ m， $A D ＝ 4$ m， $B C ＝ 12$ m， $A B ＝ 13$ m， $A D ⊥ C D$ ，求需要绿化部分的面积．

查看试题解析
19. 如图，正方形网格中的每个小正方形边长都是 $1$ ，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形（不需要写画法）．

(1)、在图 $1$ 中，画一个正方形，使它的面积是 $10$ ；

(2)、在图 $2$ 中，画一个三角形 $A B C$ ，使它的三边长分别为： $A B = \sqrt{2}$ 、 $B C = 2 \sqrt{2}$ 、 $A C = \sqrt{10}$ ，并计算 $A C$ 边上的高为．（直接写出结果）

查看试题解析
20. 观察下列各式及其验证过程：
$2 \sqrt{\frac{2}{3}} = \sqrt{2 + \frac{2}{3}}$ ，验证： $2 \sqrt{\frac{2}{3}} = \sqrt{\frac{2^{3}}{3}} = \sqrt{\frac{2^{3} - 2 + 2}{2^{2} - 1}} = \sqrt{2 + \frac{2}{3}}$ ；
$3 \sqrt{\frac{3}{8}} = \sqrt{3 + \frac{3}{8}}$ ，验证： $3 \sqrt{\frac{3}{8}} = \sqrt{\frac{3^{3}}{8}} = \sqrt{\frac{3^{3} - 3 + 3}{3^{2} - 1}} = \sqrt{3 + \frac{3}{8}}$ ．

(1)、按照上述两个等式及其验证过程的基本思路，猜想 $4 \sqrt{\frac{4}{15}}$ 的变形结果，并进行验证．

(2)、写出用n（n为任意自然数，且 $n \geq 2$ ）表示的等式反映上述各式的规律，并给出证明．

查看试题解析
21. 某校的九（1）班教室A位于工地B处的正东方向，且 $A B = 320$ 米，一辆大型货车卸货后从B处出发，沿北偏东 $60 °$ 方向的公路上行驶，试问：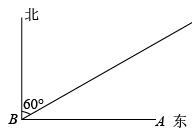

(1)、若大型货车的噪声污染半径为150米，教室A是否在大型货车的噪声污染范围内？试说明理由；

(2)、若大型货车的噪声污染半径为200米，为了不干扰九年级同学的学习，计划在货车行驶的公路一侧安装隔音板，则至少需隔音板多少米？

查看试题解析
22.

(1)、用“ $=$ ”、“ $>$ ”、“ $<$ ”填空： $4 + 3$ $2 \sqrt{4 \times 3}$ ， $1 + \frac{1}{6}$ $2 \sqrt{1 \times \frac{1}{6}}$ ， $5 + 5$ $2 \sqrt{5 \times 5}$ ．

(2)、由（1）中各式猜想 $m + n$ 与 $2 \sqrt{m n} (m \geq 0 ， n \geq 0)$ 的大小关系，并说明理由．

(3)、请利用上述结论解决下面问题：
某园林设计师要对园林的一个区域进行设计改造，将该区域用篱笆围成矩形的花圃．如图所示，花圃恰好可以借用一段墙体，为了围成面积为 $200 m^{2}$ 的花圃，所用的篱笆至少是多少米？

查看试题解析
23. 用四个全等的直角三角形拼成如图①所示的大正方形，中间也是一个正方形．它是美丽的弦图．其中四个直角三角形的直角边长分别为a，b（a＜b），斜边长为c．

(1)、结合图①，说明：a²+b²＝c²；

(2)、如图②，将这四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形ABCDEFGH．若该图形的周长为24，OH＝3，求该图形的面积；

(3)、如图③，将八个全等的直角三角形紧密地拼接成正方形PQMN，记正方形PQMN、正方形ABCD、正方形EFGH的面积分别为S₁、S₂、S₃ ，若S₁+S₂+S₃＝18，则S₂＝　　．

查看试题解析