山西省晋中市平遥县2022-2023学年八年级下学期三月月考数学试卷

试卷更新日期：2023-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列式子① $x > 0$ ；② $\frac{1}{x} < - 1$ ；③ $2 x < - 2 + x$ ；④ $x + y > - 3$ ；⑤ $x = - 1$ ，其中是一元一次不等式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 为解决部分家长在放学时间不能按时接孩子的问题，我市许多学校都启动了“课后服务”工作．某学校为了开展好课后服务，计划用不超过10000元的资金购买足球、篮球和排球用于球类兴趣班，已知足球、篮球、排球的单价分别为100元、80元、60元，且根据参加球类兴趣班的学生数了解到以下信息：①篮球的数量必须比足球多10个，②排球的数量必须是足球的3倍．则学校最多能购买足球的个数是（）

A、10 B、25 C、26 D、30

查看试题解析
3. 如图，在 $△ A B C$ 中， $A B = A C$ ，给出的下列条件中，不能使 $B D = C E$ 的是（）

A、 $B D$ ， $C E$ 分别为 $A C$ ， $A B$ 边上的高 B、 $B D$ ， $C E$ 分别为 $A C$ ， $A B$ 边上的中线 C、 $∠ A B D = \frac{1}{3} ∠ A B C ， ∠ A C E = \frac{1}{3} ∠ A C B$ D、 $∠ A B D = ∠ B C E$

查看试题解析
4. 如图，直线 $l_{1} ∥ l_{2}$ ，AB＝AC，∠BAC＝40°，则∠1＋∠2的度数是（）

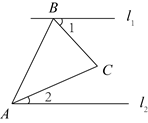A、60° B、70° C、80° D、90°

查看试题解析
5. 如图， $△ A B C$ 中， $A B = A C$ ， $D$ 是 $B C$ 中点，下列结论中错误的是（）．

A、 $∠ B = ∠ C$ B、 $A D ⊥ B C$ C、 $A D$ 平分 $∠ B A C$ D、 $A B = 2 B D$

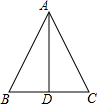查看试题解析
6. 在螳螂的示意图中，AB∥DE，△ABC是等腰三角形，∠ABC＝124°，∠CDE＝72°，则∠ACD＝（）

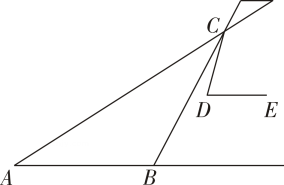A、16° B、28° C、44° D、45°

查看试题解析
7. 如图，在△ABC中，∠A＝36°，AB＝AC，BD是△ABC的角平分线.若在边AB上截取BE＝BC，连接DE，则图中等腰三角形共有（）

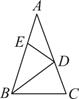A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 用反证法求证：三角形中最多有一个钝角．下列假设正确的是（）

A、假设三角形中至少有两个钝角 B、假设三角形中最多有两个钝角 C、假设三角形中最少有一个钝角 D、假设三角形中没有钝角

查看试题解析
9. 给出下列命题：①若 $a > b$ ，则 $a c^{2} > b c^{2}$ ；②若 $a b > c$ ，则 $b > \frac{c}{a}$ ；③若 $- 3 a > 2 a$ ，则 $a < 0$ ；④若 $a < b$ ，则 $a - c < b - c$ ．其中正确的是（）

A、③④ B、①③ C、①② D、②④

查看试题解析
10. 如图是“人字形”钢架，其中斜梁AB＝AC ，顶角∠BAC＝120°，跨度BC＝10m ， AD为支柱（即底边BC的中线），两根支撑架DE⊥AB ， DF⊥AC ，则DE+DF等于（　　）

A、10m B、5m C、2.5m D、9.5m

查看试题解析

二、填空题

11. 写出一个解集为x＜－1，且未知数的系数为2的一元一次不等式：.

查看试题解析
12. 已知△ABC是等腰三角形．若∠A=40°，则△ABC的顶角度数是．

查看试题解析
13. 如下图，将一个等边三角形剪去一个角后得到一个四边形，则图中 $∠ α + ∠ β$ 的度数是．

查看试题解析
14. 如下图，一把直尺压住射线 $O B$ ，另一把完全一样的直尺压住射线 $O A$ 并且与第一把直尺交于点P，小明说：“射线 $O P$ 就是 $∠ A O B$ 的平分线．”这样说的依据是．

查看试题解析
15. 如图，要使输出的y值大于100，则输入的最小正整数x是

查看试题解析

三、解答题

16. 解下列不等式，并把解集在数轴上表示出来．

(1)、 $\frac{x + 4}{3} - \frac{3 x - 1}{2} > 1$

(2)、 $2 (3 x - 2) > x + 1$ ；

查看试题解析
17. 下面是小明同学解不等式的过程，请认真阅读并完成填空。
解不等式： $\frac{2 x - 1}{3} < \frac{3 x - 2}{2} - 1$
解： $2 (2 x - 1) < 3 (3 x - 2) - 6$      第①步
$4 x - 2 < 9 x - 6 - 6$               第②步
$4 x - 9 x < - 6 - 6 + 2$              第③步
$- 5 x < - 10$                     第④步
$x < 2$                         第⑤步

(1)、以上解题过程中，第②步是依据（运算律）进行变形的；

(2)、第步开始出现错误，这一步错误的原因是；

(3)、该不等式的正确解集为．

查看试题解析
18.

(1)、①如果a－b＜0，那么ab；
②如果a－b＝0，那么ab；
③如果a－b＞0，那么ab.

(2)、由(1)你能归纳出比较a与b大小的方法吗？请用文字语言叙述出来．

(3)、用(1)的方法你能否比较3x²－3x＋7与4x²－3x＋7的大小？如果能，请写出比较过程．

查看试题解析
19. 如图，某学校（A点）与公路（直线1）的距离为300米，与车站（D点）的距离为500米，现要在公路上建一个小商店（C点），使之与学校A及车站D的距离相等．

(1)、在图中作出点C；

(2)、求商店C与车站D之间的距离．

查看试题解析
20. “端午节”是中华民族古老的传统节日．甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案．
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95% 收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90% 收费．
设某位顾客购买了x元的该种粽子．

(1)、补充表格，填写在“横线”上：
x（单位：元）
实际在甲超市的花费（单位：元）
实际在乙超市的花费（单位：元）
0＜x≤200
x
x
200＜x≤300

x
x ＞300



(2)、当x为何值时？到甲、乙两超市的花费一样．

(3)、如果顾客在“端午节”当天购买该种粽子超过300元，那么到哪家超市花费更少？说明理由．

查看试题解析
21. 图1所示的是某超市入口的双翼闸门，如图2，当它的双翼展开时，双翼边缘的端点A与B之间的距离为 $10 c m$ ，双翼的边缘 $A C = B D = 54 c m$ ，且与闸机侧立面夹角 $∠ P C A = ∠ B D Q = 30 °$ ，求当双翼收起时，可以通过闸机的物体的最大宽度．

查看试题解析
22. 综合与实践徐老师给爱好学习的小敏和小洁提出这样一个问题：如图1，在 $△ A B C$ 中， $∠ B = 2 ∠ C$ ， $A D$ 是 $∠ B A C$ 的平分线．
求证： $A B + B D = A C$ ．

(1)、解决问题：小敏的证明思路：在 $A C$ 上截取 $A E = A B$ ，连接 $D E$ ．（如图2）
小洁的证明思路：延长 $C B$ 至点E，使 $B E = A B$ ，连接 $A E$ ．（如图3）
请你任意选择一种思路完成证明．

(2)、问题升华：如图4，在 $△ A B C$ 中，若 $∠ A C B = 2 ∠ B$ ， $∠ A C B \neq 90 °$ ， $A D$ 是 $△ A B C$ 外角 $∠ C A F$ 的平分线，交 $B C$ 的延长线于点D，则线段 $A B$ ， $A C$ ， $C D$ 之间的数量关系又如何？请证明．

查看试题解析
23. 如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E.

(1)、当∠BDA=115°时，∠BAD=°；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；

(2)、当DC等于多少时，△ABD≌△DCE，请说明理由；

(3)、在点D的运动过程中，△ADE的形状也在改变，判断当∠BDA等于多少度时，△ADE是等腰三角形.

查看试题解析

x（单位：元）	实际在甲超市的花费（单位：元）	实际在乙超市的花费（单位：元）
0＜x≤200	x	x
200＜x≤300		x
x ＞300