山东省济宁市金乡县2022-2023学年八年级下学期3月月考数学试题
试卷更新日期:2023-04-20 类型:月考试卷
一、单选题
-
1. 下列二次根式中是最简二次根式的是( )A、 B、 C、 D、2. 等式 成立的x的取值范围在数轴上可表示为( )A、
 B、
B、 C、
C、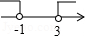 D、
D、 3. 实数a,b满足 , 则的值是( )A、2 B、 C、-6 D、4. 如图,矩形 中, , ,点 , 在数轴上,若以点 为圆心,对角线 的长为半径作弧交数轴的正半轴于点 ,则点 表示的数为( ).
3. 实数a,b满足 , 则的值是( )A、2 B、 C、-6 D、4. 如图,矩形 中, , ,点 , 在数轴上,若以点 为圆心,对角线 的长为半径作弧交数轴的正半轴于点 ,则点 表示的数为( ).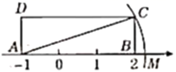 A、 B、 C、 D、5. 化简 的结果为( )A、 B、2 C、 D、6. 已知x= +2,则代数式x2﹣x﹣2的值为( )A、9+5 B、9+3 C、5+5 D、5+37. 若的整数部分为x,小数部分为y,则的值是( )A、 B、 C、1 D、38. 如图,长方体的高为 , 底面是边长为的正方形一只蚂蚁从顶点开始爬向顶点 , 那么它爬行的最短路程为( )
A、 B、 C、 D、5. 化简 的结果为( )A、 B、2 C、 D、6. 已知x= +2,则代数式x2﹣x﹣2的值为( )A、9+5 B、9+3 C、5+5 D、5+37. 若的整数部分为x,小数部分为y,则的值是( )A、 B、 C、1 D、38. 如图,长方体的高为 , 底面是边长为的正方形一只蚂蚁从顶点开始爬向顶点 , 那么它爬行的最短路程为( ) A、 B、 C、 D、9. 下列条件:①△ABC的一个外角与其相邻内角相等;②;③;④AC=n2-1,BC=2n,AB=n2+1(n>1).能判定△ABC是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个10. 先阅读下面例题的解答过程,然后作答( )
A、 B、 C、 D、9. 下列条件:①△ABC的一个外角与其相邻内角相等;②;③;④AC=n2-1,BC=2n,AB=n2+1(n>1).能判定△ABC是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个10. 先阅读下面例题的解答过程,然后作答( )例题:化简。
解:先观察 ,
由于 , 即 ,
且 , 即 ,
则有 , 试用上述例题的方法化简:
A、 B、 C、 D、二、填空题
-
11. 若最简二次根式与最简二次根式相等,则m+n= .12. 实数a、b在数轴上的位置如图所示,化简的结果是 .
 13. 若是整数,则正整数n的最小值是 .14. 如图所示的网格是正方形网格,则 .
13. 若是整数,则正整数n的最小值是 .14. 如图所示的网格是正方形网格,则 . 15. 如图,在中, , 以和为边向两边分别作正方形,面积分别为和 , 已知 , 且 , 则的长为 .
15. 如图,在中, , 以和为边向两边分别作正方形,面积分别为和 , 已知 , 且 , 则的长为 .
三、解答题
-
16. 计算.(1)、(2)、17. 如图,每个小正方形的边长都为1,的顶点均在格点上.
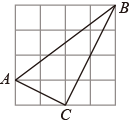 (1)、判断的形状,并说明理由;(2)、求AB边上的高h.18. 已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2 ,
(1)、判断的形状,并说明理由;(2)、求AB边上的高h.18. 已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2 ,
求:
(1)、AB的长;(2)、S△ABC .19. 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.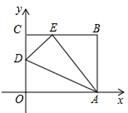 20. 如图,在等腰中, , , 以斜边为一条直角边,向外作另一直角边长为1的 , 依次作下去,记的面积为 , 的面积为 , 的面积为 , …,回答下列问题:
20. 如图,在等腰中, , , 以斜边为一条直角边,向外作另一直角边长为1的 , 依次作下去,记的面积为 , 的面积为 , 的面积为 , …,回答下列问题: (1)、 , ;(2)、求的值.21. 如图,在长方形中, , , E为边上的中点,点F从点B出发,以每秒1个单位长度的速度沿着边向终点C运动,连接 , , . 设点F运动的时间为t秒.
(1)、 , ;(2)、求的值.21. 如图,在长方形中, , , E为边上的中点,点F从点B出发,以每秒1个单位长度的速度沿着边向终点C运动,连接 , , . 设点F运动的时间为t秒. (1)、当t为何值时,?(2)、是否存在某一时刻,使得?如果存在,求出t的值;如果不存在,说明理由.22. 在学习完勾股定理这一章后,小梦和小璐进行了如下对话.
(1)、当t为何值时,?(2)、是否存在某一时刻,使得?如果存在,求出t的值;如果不存在,说明理由.22. 在学习完勾股定理这一章后,小梦和小璐进行了如下对话.小梦:如果一个三角形的三边长a,b,c满足 , 那我们称这个三角形为“类勾股三角形”,例如的三边长分别是 , 和2,因为 , 所以是“类勾股三角形”.
小璐:那等边三角形一定是“类勾股三角形”!
根据对话回答问题:
(1)、判断:小璐的说法(填“正确”或“错误”)(2)、已知的其中两边长分别为1, , 若为“类勾股三角形”,则另一边长为;(3)、如果是“类勾股三角形”,它的三边长分别为x,y,z(x,y为直角边长且 , z为斜边长),用只含有x的式子表示其周长和面积.