山东省菏泽市开发区多校联考2022-2023学年八年级下学期3月月考数学试题

试卷更新日期：2023-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列不等式中，是一元一次不等式的是（　　）

A、 $\frac{1}{x} + 1 > 2$ B、 $x^{2} > 9$ C、 $2 x + y \leq 5$ D、 $\frac{x - 5}{2} < 0$

查看试题解析
2. 下列判断错误的是（）

A、若 $a > b$ ，则 $a + 2 > b + 2$ B、若 $a > b$ ，则 $- a < - b$ C、若 $a > b$ ，则 $2 a > 2 b$ D、若 $a > b$ ，则 $a c^{2} > b c^{2}$

查看试题解析
3. 一个等腰三角形的两边长分别为3和7，这个三角形的周长是（）

A、10 B、13 C、13或17 D、17

查看试题解析
4. 用反证法证明命题“在 $△ A B C$ 中，若 $∠ B \neq ∠ C$ ，则 $A B \neq A C$ ”，首先应假设（）

A、 $A B = A C$ B、 $∠ B = ∠ C$ C、 $A B \geq A C$ D、 $∠ B \leq ∠ C$

查看试题解析
5.
如图，BE=CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还需要添加一个条件是（　　）

A、AE=DF B、∠A=∠D C、∠B=∠C D、AB=DC

查看试题解析
6. 有一个角是30°的直角三角形，斜边长度为1cm，那么斜边上的高为（）

A、 $\frac{1}{4} c m$ B、 $\frac{1}{2} c m$ C、 $\frac{\sqrt{3}}{4} c m$ D、 $\frac{\sqrt{3}}{2} c m$

查看试题解析
7. 如图，在△ABC中，AB＝AC ， ∠A＝36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（　　）

A、5个 B、4个 C、3个 D、2个

查看试题解析
8. 如图，∠AOE＝15°，OE平分∠AOB，DE∥OB交OA于点D，EC⊥OB，垂足为C．若EC＝2，则OD的长为（）

A、2 B、2 $\sqrt{3}$ C、4 D、4+2 $\sqrt{3}$

查看试题解析
9. 下面是教师出示的作图题．
已知：线段a，h，小明用如图所示的方法作 $△ A B C$ ，使 $A B = a$ ， $A B$ 上的高 $C P = h$ ．
作法：①作射线 $A M$ ，以点A为圆心、※为半径画弧，交射线 $A M$ 于点B；②分别以点A，B为圆心、△为半径画弧，两弧交于点D，E；③作直线 $D E$ ，交 $A B$ 于点P；④以点P为圆心、 $\oplus$ 为半径在 $A M$ 上方画弧，交直线 $D E$ 于点C，连接 $A C$ ， $B C$ ．
对于横线上符号代表的内容，下列说法错误的是（）

A、※代表“线段a的长” B、△代表“任意长” C、△代表“大于 $\frac{1}{2} a$ 的长” D、 $\oplus$ 代表“线段h的长”

查看试题解析
10. 已知点C在线段 $B E$ 上，分别以 $B C$ 、 $C E$ 为边作等边三角形 $A B C$ 和等边三角形 $D C E$ ， $A E$ 、 $B D$ 相交于点O，连接 $A E$ 与 $C D$ 相交于点N，连接 $B D$ 与 $A C$ 相交于点M，连接 $O C$ 、 $M N$ ，则① $A E = B D$ ；② $△ A C N ≌ △ B C M$ ；③ $∠ B O E = 120 °$ ；④ $△ M N C$ 是等边三角形；⑤ $O C$ 平分 $∠ B O E$ ；⑥ $B O = A O + C O$ ；以上结论正确的个数是（）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

11. 若(2a-1)x<2a-1的解集是x>1 ，则a 的取值范围是.

查看试题解析
12. 在实数范围内定义一种新运算“ $\oplus$ ”，其运算规则为： $a \oplus b = 2 a - 3 b$ ．如： $1 \oplus 5 = 2 \times 1 - 3 \times 5 = - 13$ ．则不等式 $x \oplus 4 < 0$ 的解集是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = A C = C D ， ∠ B A D = 60 °$ ，则 $∠ D$ 的度数为．

查看试题解析
14. 如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝4，△ABC的面积是．

查看试题解析
15. 如图，在Rt△ABC中，AC的垂直平分线DE交AC于点D，交BC于点E，∠BAE＝20°，则∠DCE的度数是为.

查看试题解析
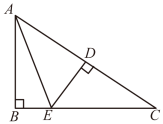16. 如图，等腰三角形ABC的底边BC长为6，面积是18，腰AC的垂直平分线EF分别交AC ， AB于E ， F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM的周长的最小值为．

查看试题解析

三、解答题

17. 解下列不等式，并把解集在数轴上表示出来．

(1)、 $\frac{x + 5}{8} - 1 < \frac{3 x + 2}{2}$ ．

(2)、 $5 x - 1 \leq 3 (x + 1)$ ．

(3)、 $3 x + 1 \geq - 5$ ．

(4)、 $1 - \frac{8 + x}{3} \geq \frac{x}{2}$ ．

查看试题解析
18. 一次数学竞赛中，共有20道题，规定答对一道题得6分，答错或不答一道题扣2分；80分以上（含80分）可以获奖，问若要获奖，至少要答对几道题？

查看试题解析
19. 在等边 $△ A B C$ 的三条边 $A B ， B C ， C A$ 上，分别取点D，E，F，使得 $A D = B E = C F$ ，连接 $D E ， E F ， F D$ ，求证： $△ D E F$ 是等边三角形．

查看试题解析
20. 如图，点C在线段AB上，AD∥EB，AC＝BE，AD＝BC，CF⊥DE于点F．

(1)、求证：△ACD≌△BEC；

(2)、求证：CF平分∠DCE．

查看试题解析
21. 已知：如图 $△ A B C$ 中 $A C = 6 c m$ ， $A B = 8 c m$ ， $B D$ 平分 $∠ A B C$ ， $C D$ 平分 $∠ A C B$ ，过D作直线平行于 $B C$ ，交 $A B$ ， $A C$ 于E，F．

(1)、求证： $△ D F C$ 是等腰三角形；

(2)、求 $△ A E F$ 的周长．

查看试题解析
22.

(1)、如图1，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：△ABD≌△CAE；

(2)、如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论△ABD≌△CAE是否成立？如成立，请给出证明；若不成立，请说明理由．

(3)、拓展应用：如图3，D，E是D，A，E三点所在直线m上的两动点（D，A，E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若∠BDA＝∠AEC＝∠BAC，求证：△DEF是等边三角形．

查看试题解析