广东省深圳市龙华区2021-2022学年八年级下学期第一次质量监测数学试卷

试卷更新日期：2023-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图案是我国几大银行的标志，其中是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 要使分式 $\frac{2}{x - 3}$ 有意义，x应满足的条件是（）

A、 $x > 3$ B、 $x < 3$ C、 $x \neq - 3$ D、 $x \neq 3$

查看试题解析
3. 一个多边形从一个顶点可引对角线3条，这个多边形内角和等于（）

A、360° B、540° C、720° D、900°

查看试题解析
4. 下列多项式中，分解因式错误的是(　　)

A、 $a^{2} + 2 a b = a (a + 2 b)$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 $a^{2} + b^{2} = (a + b)^{2}$ D、 $4 a^{2} + 4 a b + b^{2} = (2 a + b)^{2}$

查看试题解析
5. 化简 $\frac{m^{2} - 3 m}{9 - m^{2}}$ 的结果是（）

A、 $\frac{m}{m + 3}$ B、 $- \frac{m}{m + 3}$ C、 $\frac{m}{m - 3}$ D、 $\frac{m}{3 - m}$

查看试题解析
6. 如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，∠ABC=75°，则∠EAF的度数为（　　）

A、60° B、65° C、70° D、75°

查看试题解析
7. 一次环保知识竞赛共有25道题，每一题答对得4分，答错或不答都扣1分，在这次竞赛中，小明被评为优秀（85分或85分以上），小明至少要答对多少道题？如果设小明答对了x道题，根据题意列式得（　　）

A、4x-1×（25-x）＞85 B、4x+1×（25-x）≤85 C、4x-1×（25-x）≥85 D、4x+1×（25-x）＞85

查看试题解析
8. 如图，已知△ABC，按以下步骤作图：①分别以B、C为圆心，以大于 $\frac{1}{2}$ BC的长为半径作弧两弧相交于两点M、N；②作直线MN交AB于点D，连接CD．若∠B＝30°，∠A＝65°，则∠ACD的度数为（　　）

A、65° B、60° C、55° D、45°

查看试题解析
9. 如图，已知一次函数y=kx+b（k，b为常数，且k≠0）的图象与x轴交于点A（3，0），若正比例函数y=mx（m为常数，且m≠0）的图象与一次函数的图象相交于点P，且点P的横坐标为1，则关于x的不等式（k-m）x+b＜0的解集为（　　）

A、 $x < 1$ B、 $x > 1$ C、 $x < 3$ D、 $x > 3$

查看试题解析
10. 如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝ $\frac{1}{2}$ BC，连接OE，下列结论：①∠CAD＝30°；②SABCD＝AB•AC；③OB＝AB：④OE＝ $\frac{1}{4}$ BC．其中成立的有（　　）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

11. 分解因式： $3 y^{2} - 12 =$ ．

查看试题解析
12. 分式 $\frac{x - 5}{x + 5}$ 的值为 $0$ ，则 $x$ 的值为.

查看试题解析
13. 如图，∠AOP＝∠BOP，PC∥OA，PD⊥OA，若∠AOB＝45°，PC＝6，则PD的长为．

查看试题解析
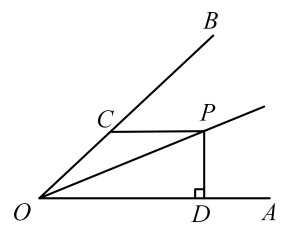14. 一个多边形的内角和是它的外角和的5倍，则这个多边形的边数为。

查看试题解析
15. 如图，已知 $a / / b / / c$ ， a与b之间的距离为3， b与c之间的距离为6， $a ， b ， c$ 分别等边三角形 $A B C$ 的三个顶点，则此三角形的边长为．

查看试题解析

三、解答题

16. 解不等式组： ${\begin{array}{l} 2 x + 9 \geq 3 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$

查看试题解析
17. 先化简，再求值 $(x - \frac{1}{x}) \div \frac{x + 1}{x}$ ，其中 $x = \sqrt{2} + 1$ .

查看试题解析
18. △ABC在平面直角坐标系xOy中的位置如图所示．
（ 1 ）作△ABC关于点C成中心对称的△A₁B₁C₁ ，
（ 2 ）将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂ ，
（ 3 ）在x轴上求作一点P，使PA₁＋PC₂的值最小，并写出点P的坐标（不写解答过程，直接写出结果）

查看试题解析
19. 如图，平行四边形ABCD的边OA在x轴上，将平行四边形沿对角线AC对折，AO的对应线段为AD，且点D，C，O在同一条直线上，AD与BC交于点E.

(1)、求证：△ABC≌△CDA.

(2)、若直线AB的函数表达式为 $y = x - 6$ ，求三角线ACE的面积.

查看试题解析
20. 某工厂准备购买A、B两种零件，已知A种零件的单价比B种零件的单价多20元，而用800元购买A种零件的数量和用600元购买B种零件的数量相等

(1)、求A、B两种零件的单价；

(2)、根据需要，工厂准备购买A、B两种零件共200件，工厂购买两种零件的总费用不超过14700元，求工厂最多购买A种零件多少件？

查看试题解析
21. 如图1，点C、D是线段AB同侧两点，且AC＝BD，∠CAB＝∠DBA，连接BC，AD交于点E.

(1)、求证：AE＝BE；

(2)、如图2，△ABF与△ABD关于直线AB对称，连接EF.
①判断四边形ACBF的形状，并说明理由；

②若∠DAB＝30°，AE＝5，DE＝3，求线段EF的长.

查看试题解析
22. 如图1，在平面直角坐标系中，直线y＝- $\frac{1}{2}$ x+b与x轴、y轴相交于A、B两点，动点C（m，0）在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．

(1)、求m和b的数量关系；

(2)、当m＝1时，如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点B′的坐标及△BCD平移的距离；

(3)、在（2）的条件下，直线AB上是否存在一点P，以P、C、D为顶点的三角形是等腰直角三角形？若存在，写出满足条件的P点坐标；若不存在，请说明理由．

查看试题解析