广东省深圳市2022-2023学年八年级下学期第一次数学检测试卷
试卷更新日期:2023-04-20 类型:月考试卷
一、单选题
-
1. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录,下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”,其中是中心对称图形的是( )A、
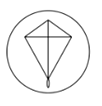 B、
B、 C、
C、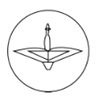 D、
D、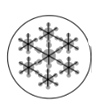 2. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、3. 已知等腰三角形的两条边长分别为4和8,则它的周长为( )A、16 B、20 C、16或20 D、144. 已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )A、
2. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、3. 已知等腰三角形的两条边长分别为4和8,则它的周长为( )A、16 B、20 C、16或20 D、144. 已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )A、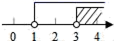 B、
B、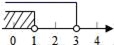 C、
C、 D、
D、 5. 等腰三角形一腰上的高与另一腰所成的角为40度,则顶角的度数为( )A、40°或65° B、50°或65° C、50°或130° D、40°或130°6. 已知不等式组 的解集为﹣1<x<1,则(a+1)(b﹣1)值为( )A、6 B、﹣6 C、3 D、﹣37. 命题:已知 , . 求证: . 运用反证法证明这个命题时,第一步应假设( )成立A、 B、 C、 D、且8. 如图,在中,为角平分线的交点,若的面积为 , 则的面积为( )
5. 等腰三角形一腰上的高与另一腰所成的角为40度,则顶角的度数为( )A、40°或65° B、50°或65° C、50°或130° D、40°或130°6. 已知不等式组 的解集为﹣1<x<1,则(a+1)(b﹣1)值为( )A、6 B、﹣6 C、3 D、﹣37. 命题:已知 , . 求证: . 运用反证法证明这个命题时,第一步应假设( )成立A、 B、 C、 D、且8. 如图,在中,为角平分线的交点,若的面积为 , 则的面积为( ) A、 B、 C、 D、9. 如图,三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF(点E在点C的左侧).下列判断正确的是( )
A、 B、 C、 D、9. 如图,三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF(点E在点C的左侧).下列判断正确的是( )结论Ⅰ:若BF=8,EC=4,则a的值为2;
结论Ⅱ:连接AD,若三角形ABC的周长为18,四边形ABFD的周长为22,则a的值为4.
 A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对10. 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对10. 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( ) A、(2,10) B、(﹣2,0) C、(2,10)或(﹣2,0) D、(10,2)或(﹣2,0)
A、(2,10) B、(﹣2,0) C、(2,10)或(﹣2,0) D、(10,2)或(﹣2,0)二、填空题
-
11. 已知点 ,将点 先向右平移4个单位长度,再向上平移6个单位长度,得到 ,则 的坐标为 .12. 如图, , 点P是的平分线上一点,交于点M,于点D,若 , 则 .
 13. 如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E,若△ADE的周长为19 cm,则BC=
13. 如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E,若△ADE的周长为19 cm,则BC= 14. 如图,已知一次函数的图象经过点和点 , 那么关于x的不等式的解集是 .
14. 如图,已知一次函数的图象经过点和点 , 那么关于x的不等式的解集是 . 15. 如图,在直角三角形中, , 且在直线l上,将绕点A顺时针旋转到位置①得到点 , 将位置①的三角形绕点P顺时针旋转到位置②得到点 , …,按此规律继续旋转,直到得到点为止(在直线l上).则:
15. 如图,在直角三角形中, , 且在直线l上,将绕点A顺时针旋转到位置①得到点 , 将位置①的三角形绕点P顺时针旋转到位置②得到点 , …,按此规律继续旋转,直到得到点为止(在直线l上).则:
三、解答题
-
16. 解不等式:(1)、;(2)、 .17. 解不等式组(1)、将不等式组的解集在数轴上表示出来;(2)、求出最小整数解与最大整数解的和.18. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).
( 1 )请按下列要求画图:

①平移△ABC,使点A的对应点A1的坐标为(-4,-3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2 .
( 2 )若将△A1B1C1绕点M旋转可得到△A2B2C2 , 请直接写出旋转中心M点的坐标 .
19. 如图,中, , , 点F为延长线上一点,点E在上,且 . (1)、求证:;(2)、若 , 求的度数.20. 已知:如图一次函数与的图象相交于点A.
(1)、求证:;(2)、若 , 求的度数.20. 已知:如图一次函数与的图象相交于点A. (1)、求点A的坐标;(2)、若一次函数与的图象与x轴分别相交于点B、C,求的面积.(3)、结合图象,直接写出时x的取值范围.21. 为了更好地治理水质.保护环境,而治污公司决定购买10台污水处理设备,现有A、B两种设备,A、B的单价分别为a万元/台和b万元/台,月处理污水分别为240吨/月和200吨/月,经调查,买一台A型设备比买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.(1)、求a、b的值;(2)、经预算,市治污公司购买污水处理器的资金不超过105万元,你认为该公司有哪几种购买方案?(3)、在(2)的条件下,若每月处理的污水不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的方案.22. 已知是边长为的等边三角形,点D是射线上的动点,将绕点A逆时针方向旋转得到 , 连接 .
(1)、求点A的坐标;(2)、若一次函数与的图象与x轴分别相交于点B、C,求的面积.(3)、结合图象,直接写出时x的取值范围.21. 为了更好地治理水质.保护环境,而治污公司决定购买10台污水处理设备,现有A、B两种设备,A、B的单价分别为a万元/台和b万元/台,月处理污水分别为240吨/月和200吨/月,经调查,买一台A型设备比买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.(1)、求a、b的值;(2)、经预算,市治污公司购买污水处理器的资金不超过105万元,你认为该公司有哪几种购买方案?(3)、在(2)的条件下,若每月处理的污水不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的方案.22. 已知是边长为的等边三角形,点D是射线上的动点,将绕点A逆时针方向旋转得到 , 连接 . (1)、如图1,猜想是什么三角形?;(直接写出结果)(2)、如图2,点D在射线上(点C的右边)移动时,证明 .(3)、点D在运动过程中,的周长是否存在最小值?若存在.请求出周长的最小值;若不存在,请说明理由.
(1)、如图1,猜想是什么三角形?;(直接写出结果)(2)、如图2,点D在射线上(点C的右边)移动时,证明 .(3)、点D在运动过程中,的周长是否存在最小值?若存在.请求出周长的最小值;若不存在,请说明理由.