安徽省蚌埠市五校联考2022-2023学年八年级下学期第一次调研数学试卷

试卷更新日期：2023-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{12}$ C、 $\sqrt{18}$ D、 $\sqrt{24}$

查看试题解析
2. 下列方程中，是一元二次方程的是（　　）

A、 $2 x^{2} - 9 = 0$ B、 $x = \frac{4}{x}$ C、 $x^{2} + 7 x - 3 y = 0$ D、 $x^{2} + 4 = (x - 1) (x - 2)$

查看试题解析
3. 下列各式计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ C、 $2 \sqrt{3} \times 3 \sqrt{3} = 6 \sqrt{3}$ D、 $\sqrt{27} \div \sqrt{3} = 3$

查看试题解析
4. 使代数式 $\frac{1}{\sqrt{x + 2}} - \sqrt{3 - 2 x}$ 有意义的整数x有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
5. 若关于x的一元二次方程 $(k - 1) x^{2} + 4 x + 1 = 0$ 有两个不相等的实数根，则k的取值范围是（）

A、 $k > 5$ B、 $k < 5$ 且 $k \neq 1$ C、 $k > - 5$ 且 $k \neq 1$ D、 $k \neq 1$

查看试题解析
6. 已知 $a = \sqrt{2023} - \sqrt{2022}$ ， $b = \sqrt{2022} - \sqrt{2021}$ ， $c = \sqrt{2021} - \sqrt{2020}$ ，那么a，b，c的大小关系是（　　）

A、 $a < b < c$ B、 $a < c < b$ C、 $c < b < a$ D、 $b < c < a$

查看试题解析
7. 如图，长方形内有两个相邻的正方形，其面积分别为6和24，则图中阴影部分面积为（）

A、5 B、 $5 \sqrt{5}$ C、6 D、 $6 \sqrt{6}$

查看试题解析
8. 若 $m = \sqrt{2 n - 5} + \sqrt{5 - 2 n} + 2$ ，则 $n^{- m} =$ （）

A、 $\frac{4}{25}$ B、 $\frac{25}{4}$ C、 $- \frac{25}{4}$ D、 $- \frac{4}{25}$

查看试题解析
9. 已知三角形的三条边为 $a ， b ， c$ ，且满足 $a^{2} - 10 a + b^{2} - 16 b + 89 = 0$ ，则这个三角形的最大边 $c$ 的取值范围是（）

A、c＞8 B、5＜c＜8 C、8＜c＜13 D、5＜c＜13

查看试题解析
10. 探讨关于x的一元二次方程 $a x^{2} + b x - 1 = 0$ 总有实数根的条件，下面三名同学给出建议：甲：a，b同号；乙： $a - b - 1 = 0$ ；丙： $a + b - 1 = 0$ ．其中符合条件的是（）

A、甲，乙，丙都正确 B、只有甲错误 C、甲，乙，丙都错误 D、只有乙正确

查看试题解析

二、填空题

11. 计算： $2 \sqrt{2} \times \frac{\sqrt{12}}{4} \div \sqrt{27} =$ ．

查看试题解析
12. 已知 $t^{2} - 3 t + 1 = 0$ ，则 $t + \frac{1}{t} =$ .

查看试题解析
13. 观察下列各式：① $2 \sqrt{\frac{2}{3}} = \sqrt{2 + \frac{2}{3}}$ ；② $3 \sqrt{\frac{3}{8}} = \sqrt{3 + \frac{3}{8}}$ ；③ $4 \sqrt{\frac{4}{15}} = \sqrt{4 + \frac{4}{15}}$ ；…；根据这些等式反映的规律，若 $x \sqrt{\frac{2023}{y}} = \sqrt{x + \frac{2023}{y}}$ ，则 $x^{2} - y =$ ．

查看试题解析
14. “通过等价变换，化陌生为熟悉，化未知为已知”是数学学习中解决问题的基本思维方，如：解方程 $x - \sqrt{x} = 0$ ，就可以利用该思维方式，设 $\sqrt{x} = y$ ，将原方程转化为： $y^{2} - y = 0$ 这个熟悉的关于y的一元二次方程，解出y，再求x，这种方法又叫“换元法”，请你用这种思维方式和换元法解方程： $x^{2} + 4 x + 4 \sqrt{x^{2} + 4 x} - 5 = 0$ ．方程的解为．

查看试题解析

三、解答题

15. 计算

(1)、 $\sqrt{12} + | \sqrt{3} - 2 | + 3 - {(π - 3.14)}^{0}$ ；

(2)、 $(4 \sqrt{8} - 2 \sqrt{\frac{1}{2}} + \sqrt{18}) \div 3 \sqrt{2}$ ．

查看试题解析
16. 解方程：

(1)、 $x^{2} - 4 x + 3 = 0$ ；

(2)、 ${(x - 3)}^{2} - 6 (x - 3) + 8 = 0$ ．

查看试题解析
17. 先化简，再求值： $(\frac{2 a}{a - 1} + \frac{a}{1 - a}) \div a$ ，其中 $a = \sqrt{10} + 1$ ．

查看试题解析
18. 阅读与思考
请仔细阅读并完成相应任务：在解决问题“已知 $a = \frac{1}{\sqrt{2} - 1}$ ，求 $3 a^{2} - 6 a - 1$ 的值”时，小明是这样分析与解答的：
∵ $a = \frac{1}{\sqrt{2} - 1} = \frac{\sqrt{2} + 1}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \sqrt{2} + 1$
∴ $. a - 1 = \sqrt{2}$ ，
∴ $a^{2} - 2 a = 1$ ，
∴ $3 a^{2} - 6 a = 3 ， 3 a^{2} - 6 a - 1 = 2$ .
任务：请你根据小明的分析过程，解决如下问题：若 $∵ a = \frac{2}{3 - \sqrt{7}}$ ，求 $2 a^{2} - 12 a + 1$ 的值.

查看试题解析
19. 已知关于x的一元二次方程 $(m - 1) x^{2} - 2 m x + m + 2 = 0$ ．

(1)、若方程有实数根，求m的取值范围；

(2)、在等腰 $△ A B C$ 中，一边长为3，其余两边长为方程的两个根，求m的值．

查看试题解析
20. 在实数范围内定义新运算“ $△$ ”，其规则为： $a △ b = a^{2} - a b$ ，根据这个规则，解决下列问题：

(1)、求 $(x + 2) △ 5 = 0$ 中x的值；

(2)、证明： $(x + m) △ 5 = 0$ 中，无论m为何值，x总有两个不同的值．

查看试题解析
21. 阅读下列解题过程：
$\frac{1}{\sqrt{5} + \sqrt{4}} = \frac{1 \times (\sqrt{5} - \sqrt{4})}{(\sqrt{5} + \sqrt{4}) (\sqrt{5} - \sqrt{4})} = \frac{\sqrt{5} - \sqrt{4}}{{(\sqrt{5})}^{2} - {(\sqrt{4})}^{2}} = \sqrt{5} - \sqrt{4} = \sqrt{5} - 2$ ，

$\frac{1}{\sqrt{6} + \sqrt{5}} = \frac{1 \times (\sqrt{6} - \sqrt{5})}{(\sqrt{6} + \sqrt{5}) (\sqrt{6} - \sqrt{5})} = \frac{\sqrt{6} - \sqrt{5}}{{(\sqrt{6})}^{2} - {(\sqrt{5})}^{2}} = \sqrt{6} - \sqrt{5}$ ．

(1)、观察上面的解题过程，请直接写出结果 $\frac{1}{\sqrt{10} - \sqrt{9}} =$ ， $\frac{1}{\sqrt{n} + \sqrt{n - 1}}$ ＝．

(2)、利用上面提供的信息请化简：
$(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2022} + \sqrt{2023}}) (\sqrt{2023} + 1)$ 的值．

查看试题解析
22. $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 5 cm$ ， $B C = 6 cm$ ，点P从点A开始沿边 $A B$ 向终点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边 $B C$ 向终点C以2cm/s的速度移动.如果点P、Q分别从点A、B同时出发，当点Q运动到点C时，两点停止运动.设运动时间为t秒.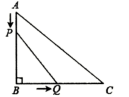

(1)、填空： $B Q =$ ， $P B =$ （用含t的代数式表示）；

(2)、是否存在t的值，使得 $△ P B Q$ 的面积等于 $4 {cm}^{2}$ ？若存在，请求出此时t的值；若不存在，请说明理由.

查看试题解析
23. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0$ $(a \neq 0)$ 有两个实数根，其中一个实数根是另一个实数根的2倍，那么称这样的方程是“倍根方程”．例如一元二次方程 $x^{2} - 6 x + 8 = 0$ 的两个根是 $x_{1} = 2 ， x_{2} = 4$ ，则方程 $x^{2} - 6 x + 8 = 0$ 是“倍根方程”．

(1)、通过计算，判断 $x^{2} - 3 x + 2 = 0$ 是否是“倍根方程”．

(2)、若关于x的方程 $（ x - 2 ） (x - m) = 0$ 是“倍根方程”，求代数式 $m^{2} + 2 m + 2$ 的值；

(3)、已知关于x的一元二次方程 $x^{2} - (m - 1) x + 32 = 0$ （m是常数）是“倍根方程”，请直接写出m的值．

查看试题解析