河北省石家庄市赵县2022-2023学年第一学期七年级数学期末试卷
试卷更新日期：2023-04-20 类型：期末考试
一、 选择题(本大题共16个小题．1- 10小题每题3分，11- 16小题每题2分，共42分．)
-
1. 圆圆想了解某地某天的天气情况，在某气象网站查询到该地这天的最低气温为-6℃，最高气温为2℃，则该地这天的温差（最高气温与最低气温的差）为（ ）
A、-8℃ B、-4℃ C、4℃ D、8℃2. 实数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（ ）
A、a<-2 B、b<1 C、a>b D、-a>b3. 厂家检测甲、乙、丙、丁四个足球的质量，超过标准质量的克数记为正数，不足标准质量的克数记为负数，结果如图所示，其中最接近标准质量的足球是（ ）
A、甲 B、乙 C、丙 D、丁4. 如图，用圆规比较两条线段AB和A'B的长短，其中正确的是（ ）
A、A'B'> AB B、A'B'=AB C、A'B'<AB D、没有刻度尺，无法确定5. 不一定相等的一组是（ ）A、a+b与b+a B、3a与a+a+a C、a3与a·a·a D、3(a+b)与3a+b6. 中国有悠久的金石文化，印信是金石文化的代表之一，南北朝时期的官员独孤信的印信是迄今发现的中国古代唯一一枚楷书印．它的表面均由正方形和等边三角形组成(如图1)，可以看成图2所示的几何体．从正面看该几何体得到的平面图形是（ ）
A、
B、
C、
D、
7. 在计算：M-(5x2-3x-6)时，嘉琪同学将括号前面的“-”号抄成了“+”号，得到的运算结果是-2x2+3x-4，你认为多项式M是（ ）A、-7x2+6x+2 B、-7x2-6x-2 C、-7x2+6x-2 D、-7x2-6x+28. 下列等式变形正确的是（ ）A、若4x=2，则x=2 B、若4x-2=2-3x，则4x+3x=2-2 C、若4(x+1)-3=2(x+1)，则4(x+1)+2(x+1)=3 D、若=1，则3(3x+1)-2(1-2x)=69. 按照如图所示的操作步骤进行计算，若输人的值为-3，则输出的值为（ ）
A、0 B、4 C、55 D、6010. 下列四个生活、生产现象：①用四个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路改直，就能缩短路程，
其中可用基本事实“两点之间，线段最短”来解释的现象有（ ）
A、①② B、①③ C、②④ D、③④11. 2022年6月，河北省教育厅提出全面建立初中学业水平考试制度，体育与健康科目纳入考试范围，为加强锻炼，小刚、小强两人练习赛跑，小刚每秒跑7米，小强每秒跑6.5米，小刚让小强先跑5米，设x秒钟后，小刚追上小强，下列四个方程中不正确的是（ ）A、7x=6.5x+5 B、7x-5=6.5 C、(7-6.5)x=5 D、6.5x=7x-512. 如图，将一个三角板60°角的顶点与另一个三角板的直角顶点重合，∠1=27°40'，∠2的大小是（ ）
A、27°40' B、57°40' C、58°20' D、62°20'13. 北京大兴国际机场采用“三纵一横"全向型跑道构型，可节省飞机飞行时间，遇极端天气侧向跑道可提升机场运行能力．跑道的布局为：三条南北向的跑道和一条偏东南走向的侧向跑道．如图，侧向跑道AB在点O南偏东70°的方向上，则这条跑道所在射线OB与正北方向所成角的度数为（ ）
A、20° B、70° C、110° D、160°14. 嘉琪在进行解方程的思维训练，其中有一个方程“2y-=y+■”中的■没印清晰，嘉琪问老师，老师只是说：“■是一个有理数，该方程的解与当×= 2时代数式5(x-1)-2(x- 2)-4的值相同．”嘉琪很快补上了这个有理数．你认为嘉琪补的这个有理数是（ ）A、1 B、-1 C、2 D、-215. 历史上数学家欧拉最先把关于x的多项式用记号f(x)来表示，把x等于某数a时的多项式的值用f(a)来表示．例如，对于多项式f(x)=mx3+nx+5，当x=2时，多项式的值为f(2) = 8m+2n+5，若f(2)=6，则f(-2)的值为（ ）A、2 B、-2 C、4 D、-416. “曹冲称象”是流传很广的故事，如图．按照他的方法：先将象牵到大船上，并在船侧面标记水位，再将象牵出．然后往船上抬入20块等重的条形石，并在船上留3个搬运工，这时水位恰好到达标记位置．如果再抬人1块同样的条形石，船上只留1个搬运工，水位也恰好到达标记位置．已知搬运工体重均为120斤，设每块条形石的重量是x斤，则正确的是（ ）
A、依题意3×120=x-120 B、依题意20x+3×120=(20+1)x+ 120 C、该象的重量是5040斤 D、每块条形石的重量是260斤二、填空题(本大题共3个小题，每小题3分，共9分．其中18小题第一空2分，第二空1分；19小题第一空1分，第二空2分．)
-
17. 已知线段AB=4，在直线AB上作线段BC，使得BC=2，若D是线段AC的中点，则线段AD的长为18. 某书店新进了一批图书，甲．乙两种书的进价分别为4元/本、10元/本．现购进m本甲种书和n本乙种书，共付款P元(1)、用含m，n的代数式表示P，则P=(2)、若共购进5×104本甲种书及3×103本乙种书，用科学记数法表示P的值，则P=19. 如图，棋盘旁有甲．乙两个围棋盒．
(1)、甲盒中都是黑子，共10个，乙盒中都是白子，共8个，嘉嘉从甲盒拿出a个黑子放入乙盒，使乙盒棋子总数是甲盒所剩棋子数的2倍，则a=(2)、设甲盒中都是黑子，共m(m>2)个，乙盒中都是白子，共2m个，嘉嘉从甲盒拿出a(1<a<m)个黑子放入乙盒中，此时乙盒棋子总数比甲盒所剩棋子数多三、解答题(本大题共7个小题，共69分.)
-
20. 四个有理数A、B、C、D，其中，与6相加得0的数是A，C是的倒数．(1)、如果A+C=2B，求B的值：(2)、如果A×B= D，求D的值：(3)、计算：(A-D)×C÷B．21. 如图是一个正方体的表面展开图，请回答下列问题：
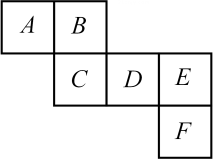(1)、与面B、C相对的面分别是(2)、若A=a3+a2b+3，B=a2b-3，C=a3-1，D=-(a2b-6)，且相对两个面所表示的代数式的和都相等，求E、F分别代表的代数式．22. 如图，已知平面上四个点A，B，C，D，请按要求完成下列问题：
⑴画直线AB，射线BD，连接AC；
⑵在线段AC上求作点P ，使得CP=AC-AB；(保留作图痕迹)
⑶请在直线AB上确定一点Q，使点Q 到点P与点D的距离之和最短．
23. 在数学课上，老师展示了下列问题，请同学们分组讨论解决的方法．中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有这样一个问题：“今有三人共车，二车空；二人共车，九人步，问人和车各几何？”这个题的意思是：今有若干人乘车．若每3人乘一辆车，则余2辆空车；若每2人乘一辆车．则余9人需步行，问共有多少辆车，多少人？
某小组选择用一元一次方程解决问题，请补全他们的分析和解答过程：
设共有x辆车；
(1)、由“若每3人乘一辆车，则余2辆空车”，可得人数为(用含x的式子表示)；(2)、由“若每2人乘一辆车，则余9人需步行”．可得人数为(用含x的式子表示)；(3)、根据两种乘车方式的人数相等，列出方程为(4)、写出解方程的过程．24. 嘉嘉和琪琪在玩一个圆珠游戏，如图，三个圆珠可以在槽内左右滚动．当圆珠发生碰撞时，就得到相撞圆珠上的代数式所表示数的和y．当三个圆珠同时相撞时，不论x的值为多大，y的值总不变．
(1)、求a的值；(2)、若x是一个整数，当某些圆珠相撞时，得到y的值都恰好为-1，求x的值．25. 定义：若a+b=2，则称a与b是关于2的平衡数．(1)、3与是关于2的平衡数，7-x与是关于2的平衡数． (填一个含x的代数式)(2)、若a=x2-4x-1，b=x2-2(x2-2x-1)+1，判断a与b是否是关于2的平衡数，并说明理由．(3)、若c=kx+1，d=x-3，且c与d是关于2的平衡数，若x为正整数，求非负整数k的值．26. 阅读下面材料：嘉琪遇到这样一个问题：如图1，2 AOB=α，请画一个∠AOC，使∠AOC与∠BOC互补．
嘉琪是这样思考的：首先通过分析明确射线OC在∠AOB的外部，画出示意图，如图2所示：然后通过构造平角找到∠AOC的补角∠COD，如图3所示：进而分析要使∠AOC与∠BOC互补，则需∠BOC=∠COD．
因此，嘉琪找到了解决问题的方法：反向延长射线OA得到射线OD，利用量角器画出∠BOD的平分线OC ．这样就得到了∠BOC与∠AOC互补．
(1)、嘉琪根据自己的画法写出了已知和求证，请你完成证明：已知：如图3，点O在直线AD上，射线OC平分∠BOD．
求证：∠AOC与∠BOC互补．
(2)、参考嘉琪的画法，请在图4中画出一个∠AOH，使∠AOH与∠BOH互余，(3)、已知∠EPQ和∠FPQ互余，射线PM平分∠EPQ，射线PN平分∠FPQ．若∠EPQ=β(0°<β<90°)，直接写出锐角∠MPN的度数是