苏科版数学八年级下学期复习微专题训练11 正方形的判定与性质
试卷更新日期：2023-04-19 类型：复习试卷
一、单选题（每题3分，共24分）
-
1. 正方形具有而矩形不一定具有的性质是（ ）A、四个角都为直角 B、对角线互相平分 C、对角线相等 D、对角线互相垂直2. 下列条件中，能使菱形 为正方形的是（ ）A、 B、 C、 D、 平分3. 正方形､菱形､矩形都具有的性质是（ ）A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分一组对角4. 如图，在正方形ABCD中， ， E为AB边上一点，点F在BC边上，且 ， 将点E绕着点F顺时针旋转90°得到点G，连接DG，则DG的长的最小值为（ ）
A、2 B、 C、3 D、5. 如图，以Rt△ABC的斜边BC为边，在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO.若AB＝2，AO＝ ，则AC的长等于（ ）
A、 B、8 C、 D、6. 如图，在直角坐标系中，正方形ABCD如图摆放，若顶点A，B的坐标分别为 ， ， 则顶点D的坐标为（ ）
A、 B、 C、 D、7. 如图.已知正方形ABCD的边长为12，BE＝EC，将正方形的边CD沿DE折叠到DF，延长EF交AB于G，连接DG.现有如下3个结论；①AG+EC＝GE；②∠GDE＝45°；③△BGE的周长是24.其中正确的个数为（ ）
A、0 B、1 C、2 D、38. 如图，两个正方形的边长都为6，其中正方形 绕着正方形 的对角线的交点 旋转，正方形 与边 、 分别交于点 、 （不与端点重合），设两个正方形重叠部分形成图形的面积为 ， 的周长为 ，则下列说法正确的是（ ）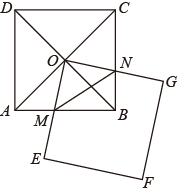
A、 发生变化， 存在最大值 B、 发生变化， 存在最小值 C、 不发生变化， 存在最大值 D、 不发生变化， 存在最小值二、填空题（每空3分，共27分）
-
9. 如图，四边形ABCD是正方形，按如下步骤操作：①分别以点A、D为圆心，以AD长为半径画弧，两弧交于点P，连接AP、DP；②连接BP、CP，则∠PBC＝ ．
10. 如图，正方形和正方形的边长分别为4和2，正方形绕点C旋转，则 ．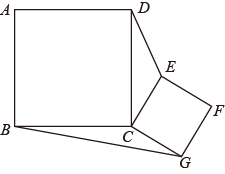
11. 如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF.连接CF交BD于G，连接BE交AG于点H.若正方形的边长为2，则线段DH长度的最小值是.
12. 如图，已知正方形的边长为1，点是边上一动点，连接 ， 将绕点顺时针旋转90°到EF，连接、 ， 则的最小值等于.
13. 欧几里得在《几何原本》中，记载了用图解法解方程x2+ax＝b2的方法，类似地我们可以用折纸的方法求方程x2+x﹣1＝0的一个正根.如图，一张边长为1的正方形的纸片ABCD，先折出AD，BC的中点E，F，再沿过点A的直线折叠使AD落在线段AF上，点D的对应点为点H，折痕为AG，点G在边CD上，连接GH，GF，线段BF、DG、CG和GF中，长度恰好是方程x2+x﹣1＝0的一个正根的线段为.
14. 如图，Rt△ABC中，四边形DBFE、GFIH都是正方形，已知AD＝1cm，DB＝3cm，则图中阴影部分面积为cm2.
15. 如图，正方形在第一象限，点、 ， 则点的坐标是 ． （用含、、的代数式表示）
16. 小明发现妈妈的耳环设计非常巧妙，如图1所示，其形状像中国数学家赵爽使用的弦图，用该弦图证明勾股定理在数学史上有着重要地位，将耳环中弦图顺时针旋转得到如图2图形，若这四个全等的直角三角形都有一个角为 ， 且 ， 则面积为；将多个弦图如图3摆放，使得顶点 ， ， ， …， ， ， ， ， …，分别在直线和x轴上，则正方形的面积是.
三、作图题（共9分）
-
17. 如图，正方形网格中的每个小正方形边长都是l，每个小格的顶点叫做格点.以格点为顶点分别按下列要求画图：
(1)、画出一个平行四边形，使其面积为6；(2)、画出一个菱形，使其面积为4.(3)、画出一个正方形，使其面积为5.四、解答题（共7题，共60分）
-
18. 如图， 分别是 各边的中点.
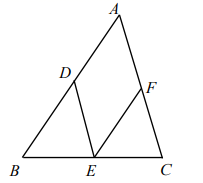(1)、四边形 是怎样的四边形？证明你的结论.(2)、若 ，且 ，判断四边形 是怎样的四边形？证明你的结论.19. 如图，正方形ABCD，E为平面内一点，且∠BEC＝90°，把△BCE绕点B逆时针旋转90°得△BAG，直线AG和直线CE交于点F.
(1)、证明：四边形BEFG是正方形；(2)、若CE＝CF，则∠AGD＝°.20. 已知在平行四边形ABCD中，点E、F分别在AB、BC边上，DE＝AF，DE⊥AF于点G．
(1)、如图1，若∠BAD＝90°，求证：四边形ABCD是正方形；(2)、在（1）的条件下，延长CB到点H，使得BH＝AE，判断△AHF的形状，并说明理由．(3)、如图2，若AB=AD，∠AED＝60°，AE＝6，BF＝2，求DE的长．21. 如图，点E，F分别在正方形ABCD的边CD，BC上，且DE=CF，点P在射线BC上（点P不与点F重合）.将线段EP绕点E顺时针旋转90得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q.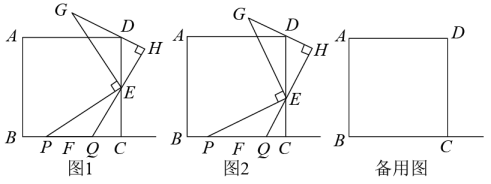
(1)、如图①，若点E是CD的中点，点P在线段BF上，则线段BP，QC，EC的数量关系为；(2)、如图②，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立.若成立，请写出证明过程；若不成立，请说明理由；(3)、若正方形ABCD的边长为6，AB=3DE，CQ=1，请直接写出线段BP的长.22. 知识再现：已知，如图，四边形ABCD是正方形，点M、N分别在边BC、CD上，连接AM、AN、MN，∠MAN＝45°，延长CB至G使BG＝DN，连接AG，根据三角形全等的知识，我们可以证明MN＝BM+DN．
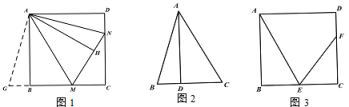(1)、知识探究：在如图中，作AH⊥MN，垂足为点H，猜想AH与AB有什么数量关系？并证明；(2)、知识应用：（2）如图，已知∠BAC＝45°，AD⊥BC于点D，且BD＝2，AD＝6，则CD的长为；(3)、知识拓展：如图，四边形ABCD是正方形，E是边BC的中点，F为边CD上一点，∠FEC＝2∠BAE，AB=24，求DF的长．23.(1)、【方法回顾】
如图1，过正方形ABCD的顶点A作一条直线l交边BC于点P，BE⊥AP于点E，DF⊥AP于点F，若DF＝2.5，BE＝1，则EF＝ ．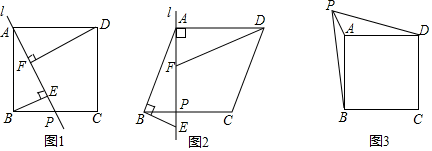
(2)、【问题解决】
如图2，菱形ABCD的边长为1.5，过点A作一条直线l交边BC于点P，且∠DAP＝90°，点F是AP上一点，且∠BAD+∠AFD＝180°，过点B作BE⊥AB，与直线l交于点E，若EF＝1，求BE的长．(3)、【思维拓展】
如图3，在正方形ABCD中，点P在AD所在直线上的上方，AP＝2，连接PB，PD，若△PAD的面积与△PAB的面积之差为m（m＞0），则PB2﹣PD2的值为 ． （用含m的式子表示）24. 如图1，在正方形ABCD和正方形BEFG中，点A，B，E在同一条直线上，P是线段DF的中点，连接PG，PC.
(1)、探究PG与PC的位置关系及的值；（写出结论，不需要证明）(2)、如图2，将原问题中的正方形ABCD和正方形BEFC换成菱形ABCD和菱形BEFG，且∠ABC＝∠BEF＝60°，探究PG与PC的位置关系及的值.写出你的猜想并加以证明；(3)、如图3，将图2中的菱形BEFG绕点B顺时针旋转.使菱形BEFG的边BG恰好与菱形ABCD的边AB在同一条直线上，问题（2）中的其他条件不变，你在（2）中得到的两个结论是否发生变化？写出你的猜想并加以证明.
-