苏科版数学八年级下学期复习微专题训练9 矩形的判定与性质
试卷更新日期:2023-04-19 类型:复习试卷
一、单选题(每题3分,共24分)
-
1. 下列条件中,不能判定平行四边形ABCD为矩形的是( )A、∠A=∠C B、∠A=∠B C、AC=BD D、AB⊥BC2. 下面性质中矩形具有而菱形没有的是( )A、对角线相等 B、邻边相等 C、对角线垂直 D、对边相等3. 在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=60°,OB=2cm,那么矩形ABCD的面积为( )A、cm B、2cm C、3cm D、4cm4. 如图,在矩形ABCD中,对角线AC、BD相交于点O,DE⊥AC于点E,∠AOD=110°,则∠CDE的大小是( )
 A、55° B、40° C、35° D、20°5. 如图,将矩形沿对角线折叠,使点落在处,交于点.若 , 则的度数为( )
A、55° B、40° C、35° D、20°5. 如图,将矩形沿对角线折叠,使点落在处,交于点.若 , 则的度数为( ) A、 B、 C、 D、6. 如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A、 B、 C、 D、6. 如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE7. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )
A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE7. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )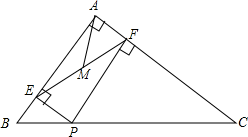 A、 B、 C、 D、8. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A、 B、 C、 D、8. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )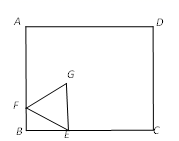 A、3 B、2.5 C、4 D、2
A、3 B、2.5 C、4 D、2二、填空题(每空3分,共24分)
-
9. 如图,矩形ABCD的对角线AC、BD相交于点O,∠BOC=120°,AC=6.则AB= .
 10. 如图,在矩形ABCD中,E是BC延长线上一点,连接AC,DE,BE=AC,若∠ACB=40°,则∠E的度数是.
10. 如图,在矩形ABCD中,E是BC延长线上一点,连接AC,DE,BE=AC,若∠ACB=40°,则∠E的度数是. 11. 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,若所围成的四边形EFGH是矩形,则原四边形ABCD需满足的条件是.(只需写出一个符合要求的条件)
11. 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,若所围成的四边形EFGH是矩形,则原四边形ABCD需满足的条件是.(只需写出一个符合要求的条件)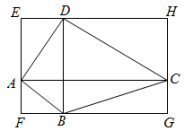 12. 在矩形ABCD中,对角线AC、BD相交于点O,AO=6cm,则BD=cm.13. 如图,▱AFDE的顶点F在矩形ABCD的边BC上,点F与点B、C不重合,若△AED的面积为4,则图中阴影部分两个三角形的面积和为.
12. 在矩形ABCD中,对角线AC、BD相交于点O,AO=6cm,则BD=cm.13. 如图,▱AFDE的顶点F在矩形ABCD的边BC上,点F与点B、C不重合,若△AED的面积为4,则图中阴影部分两个三角形的面积和为. 14. 如图,在△ABC中,∠C=90°,AC=6,BC=8,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于.
14. 如图,在△ABC中,∠C=90°,AC=6,BC=8,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于. 15. 如图,矩形 中, ,点 是 上的一点,且 , 的垂直平分线交 的延长线于点 ,连结 交 于点 .若 是 的中点,则 的长是.
15. 如图,矩形 中, ,点 是 上的一点,且 , 的垂直平分线交 的延长线于点 ,连结 交 于点 .若 是 的中点,则 的长是.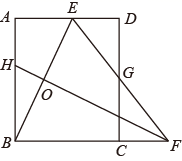 16. 如图,正方形 的边长为 , 为 上一点,且 , 为 边上的一个动点连接 ,以 为边向右侧作等边 ,连接 ,则 的最小值为.
16. 如图,正方形 的边长为 , 为 上一点,且 , 为 边上的一个动点连接 ,以 为边向右侧作等边 ,连接 ,则 的最小值为.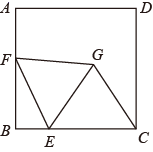
三、解答题(共8题,共72分)
-
17. 如图,将长方形ABCD沿EF折叠,使点D与点B重合.
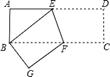 (1)、若∠AEB=40°,求∠BFE的度数;(2)、若AB=6,AD=18,求CF的长.18. 如图,在▱ABCD中,点E、F在AD边上,且BF=CE,AE=DF.
(1)、若∠AEB=40°,求∠BFE的度数;(2)、若AB=6,AD=18,求CF的长.18. 如图,在▱ABCD中,点E、F在AD边上,且BF=CE,AE=DF. (1)、求证:△ABF≌△DCE;(2)、求证:四边形ABCD是矩形.19. 如图,菱形ABCD的对角线相交于O点,DEAC,CEBD.
(1)、求证:△ABF≌△DCE;(2)、求证:四边形ABCD是矩形.19. 如图,菱形ABCD的对角线相交于O点,DEAC,CEBD. (1)、求证:四边形OCED是矩形;(2)、若AD =5,BD =8,计算DE的值.20. 如图,已知正方形 点 在 边上,以 为边在 左侧作正方形 ;以 为邻边作平行四边形 连接 .
(1)、求证:四边形OCED是矩形;(2)、若AD =5,BD =8,计算DE的值.20. 如图,已知正方形 点 在 边上,以 为边在 左侧作正方形 ;以 为邻边作平行四边形 连接 .
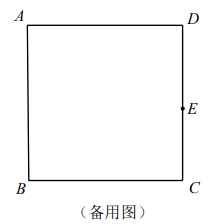 (1)、判断 和 的数量及位置关系,并说明理由;(2)、将 绕点 顺时针旋转 ,在旋转过程中, 和 的数量及位置关系是否发生变化?请说明理由.21. 操作:第一步:如图1,对折长方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开.
(1)、判断 和 的数量及位置关系,并说明理由;(2)、将 绕点 顺时针旋转 ,在旋转过程中, 和 的数量及位置关系是否发生变化?请说明理由.21. 操作:第一步:如图1,对折长方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开.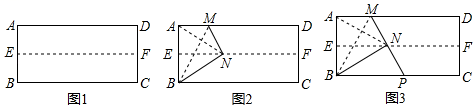
第二步:如图2,再一次折叠纸片,使点A落在EF上的N处,并使折痕经过点B,得到折痕BM,同时得到线段BN.连结AN,易知△ABN的形状是 ▲ .
论证:如图3,若延长MN交BC于点P,试判定△BMP的形状,请说明理由.
22. 如图,平行四边形中, , .对角线 , 相交于点 , 将直线绕点顺时针旋转 , 分别交直线、于点、. (1)、当°,四边形是平行四边形;(2)、在旋转的过程中,从、、、、、中任意找4个点为顶点构造四边形.
(1)、当°,四边形是平行四边形;(2)、在旋转的过程中,从、、、、、中任意找4个点为顶点构造四边形.① ▲ °,构造的四边形是菱形;
②若构造的四边形是矩形,则不同的矩形应该有 ▲ 个.
23. 如图,在平面直角坐标系中,点O为坐标原点,AB∥OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.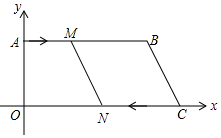 (1)、在t=3时,M点坐标 , N点坐标 ;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.24.(1)、【方法回顾】
(1)、在t=3时,M点坐标 , N点坐标 ;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.24.(1)、【方法回顾】
如图1,过正方形ABCD的顶点A作一条直线l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,若DF=2.5,BE=1,则EF= .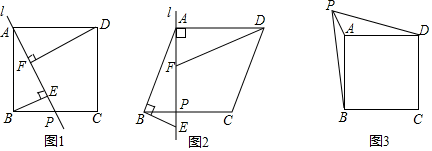 (2)、【问题解决】
(2)、【问题解决】
如图2,菱形ABCD的边长为1.5,过点A作一条直线l交边BC于点P,且∠DAP=90°,点F是AP上一点,且∠BAD+∠AFD=180°,过点B作BE⊥AB,与直线l交于点E,若EF=1,求BE的长.(3)、【思维拓展】
如图3,在正方形ABCD中,点P在AD所在直线上的上方,AP=2,连接PB,PD,若△PAD的面积与△PAB的面积之差为m(m>0),则PB2﹣PD2的值为 . (用含m的式子表示)