苏科版数学八年级下学期复习微专题训练8 平行四边形的判定与性质
试卷更新日期:2023-04-19 类型:复习试卷
一、单选题(每题2分,共16分)
-
1. 下列条件中,能判定四边形是平行四边形的条件是( )A、一组对边平行,另一组对边相等 B、一组对边平行,一组对角相等 C、一组对边平行,一组邻角互补 D、一组对边相等,一组邻角相等2. 能判定四边形ABCD为平行四边形的条件是 ( )A、CB=CD,AB=AD B、 C、AB//CD,AD=BC D、AB=CD,AD=BC3. 如图,平行四边形ABCD中,∠A的平分线AE交CD于E, 若AB=5,BC=3,则EC的长为( )
 A、1 B、2 C、2.5 D、44. 如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=( )
A、1 B、2 C、2.5 D、44. 如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=( )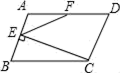 A、54° B、60° C、66° D、72°5. 如图,点P为▱ABCD外一点,连接PA、PB、PC、PD,若△APB的面积为18,△APD的面积为5,则△APC的面积为( )
A、54° B、60° C、66° D、72°5. 如图,点P为▱ABCD外一点,连接PA、PB、PC、PD,若△APB的面积为18,△APD的面积为5,则△APC的面积为( )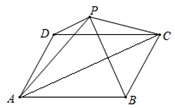 A、10 B、13 C、18 D、206. 如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( )
A、10 B、13 C、18 D、206. 如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( ) A、 B、4 C、 D、7. 对于命题“在同一平面内,若 , ,则 ”,用反证法证明,应假设( )A、 B、 C、 与 相交 D、 与 相交8. 用反证法证明命题“若在中, , 则”时,首先应假设( )A、 B、 C、 D、
A、 B、4 C、 D、7. 对于命题“在同一平面内,若 , ,则 ”,用反证法证明,应假设( )A、 B、 C、 与 相交 D、 与 相交8. 用反证法证明命题“若在中, , 则”时,首先应假设( )A、 B、 C、 D、二、填空题(每空2分,共16分)
-
9. 用反证法证明某一命题的结论“ ”时,应假设.10. 用反证法证明:“多边形中最多有三个锐角”的第一步是:假设11. 平行四边形ABCD中,∠A:∠B=2:7,则∠C=°12. 在平面直角坐标系中,▱ABCD的顶点A、B、C的坐标分别是(0,2)、(﹣3,﹣4)、(2,﹣4),则顶点D的坐标是 .13. 如图,在平行四边形 ABCD中,AD=7,AB=5,DE平分∠ADC交BC于点E,则BE的长是 .
 14. 如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=3,CF=4,则CD=.
14. 如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=3,CF=4,则CD=. 15. 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,若所围成的四边形EFGH是矩形,则原四边形ABCD需满足的条件是.(只需写出一个符合要求的条件)
15. 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,若所围成的四边形EFGH是矩形,则原四边形ABCD需满足的条件是.(只需写出一个符合要求的条件)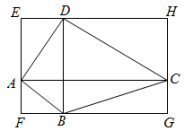 16. 如图,在平行四边形 中,对角线 、 相交于点 , , 是 边的中点, 、 为 上的点,连接 和 ,若 , , ,则图中阴影部分的面积为.
16. 如图,在平行四边形 中,对角线 、 相交于点 , , 是 边的中点, 、 为 上的点,连接 和 ,若 , , ,则图中阴影部分的面积为.
三、解答题(共11题,共107分)
-
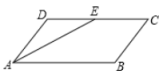
17. 用反证法证明:等腰三角形的底角是锐角.18. 如图所示,点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点,求证:四边形EFGH是平行四边形.
小明同学做法是:连接BD,利用三角形的中位线定理证明得出 , EH=FG,从而得到四边形EFGH是平行四边形.
请你完成小明的做法:
证明:连接BD,
 19. 已知点E、F分别为平行四边形ABCD的边AD、BC的中点,求证:四边形EBFD为平行四边形.
19. 已知点E、F分别为平行四边形ABCD的边AD、BC的中点,求证:四边形EBFD为平行四边形. 20. 已知:如图,E、F是▱ABCD的对角线AC上的两点,AE=CF.
20. 已知:如图,E、F是▱ABCD的对角线AC上的两点,AE=CF.求证:
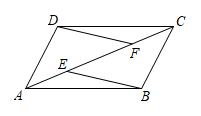 (1)、△ADF≌△CBE;(2)、EB∥DF.21. 如图,平行四边形ABCD的对角线AC,BD相交于О点,于E点,于F.
(1)、△ADF≌△CBE;(2)、EB∥DF.21. 如图,平行四边形ABCD的对角线AC,BD相交于О点,于E点,于F. (1)、求证:四边形DEBF为平行四边形;(2)、若 , , , 求的面积.22. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.(1)、如图1,当点E恰好在AC上时,求∠CDE的度数;
(1)、求证:四边形DEBF为平行四边形;(2)、若 , , , 求的面积.22. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.(1)、如图1,当点E恰好在AC上时,求∠CDE的度数;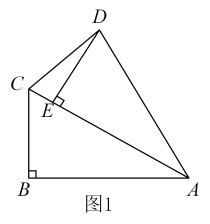 (2)、如图2,若=60° 时,点F是边AC中点,求证:四边形BFDE是平行四边形;
(2)、如图2,若=60° 时,点F是边AC中点,求证:四边形BFDE是平行四边形;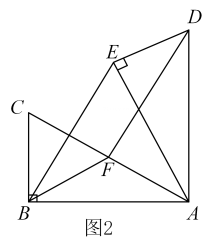 (3)、当BC=2时,连接CE,CD,设△CDE的面积为S.在旋转过程中,S是否存在最大值?若存在,请直接写出S的最大值;若不存在,请说明理由.23. 如图,矩形ABCD中,AB=4,∠ADB=30°.一动点P从B点出发沿对角线BD方向以每秒2个单位长度的速度向点D匀速运动,同时另一动点Q从D点出发沿从DC方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P、Q运动的时间为t秒(t>0).过点P作PE⊥BC于点E,连接EQ,PQ.
(3)、当BC=2时,连接CE,CD,设△CDE的面积为S.在旋转过程中,S是否存在最大值?若存在,请直接写出S的最大值;若不存在,请说明理由.23. 如图,矩形ABCD中,AB=4,∠ADB=30°.一动点P从B点出发沿对角线BD方向以每秒2个单位长度的速度向点D匀速运动,同时另一动点Q从D点出发沿从DC方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P、Q运动的时间为t秒(t>0).过点P作PE⊥BC于点E,连接EQ,PQ. (1)、求证:PE=DQ;(2)、四边形PEQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)、当t为何值时,△PQE为直角三角形?请说明理由.24. 【教材呈现】下图是华师版八年级下册数学教材第77页的部分内容.
(1)、求证:PE=DQ;(2)、四边形PEQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)、当t为何值时,△PQE为直角三角形?请说明理由.24. 【教材呈现】下图是华师版八年级下册数学教材第77页的部分内容.平行四边形的性质定理3:行四边形的对角线互相平分。
我们可以用演绎推理证明这个结论。
已知:如图,的对角线AC和BD相交于点O。
求证:OA=OC,OB=OD。
 (1)、请根据教材中的分析,结合图1写出“平行四边形的对角线互相平分”这一性质的完整的证明过程.
(1)、请根据教材中的分析,结合图1写出“平行四边形的对角线互相平分”这一性质的完整的证明过程.证明:
 (2)、
(2)、【性质应用】
如图2,的对角线相交于点 , 过点且与分别相交于点 ,
求证:;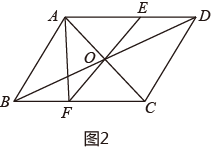 (3)、连结 , 若 , 周长是 , 则的周长是.25. 如图,在平面直角坐标系中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.
(3)、连结 , 若 , 周长是 , 则的周长是.25. 如图,在平面直角坐标系中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点. (1)、用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)、若四边形PQOB的面积是 , 且 , 试求点P的坐标,并求出直线PA与PB的函数表达式;(3)、在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.26. 如图,在平面直角坐标系中,点O为坐标原点,AB∥OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
(1)、用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)、若四边形PQOB的面积是 , 且 , 试求点P的坐标,并求出直线PA与PB的函数表达式;(3)、在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.26. 如图,在平面直角坐标系中,点O为坐标原点,AB∥OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.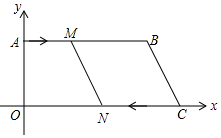 (1)、在t=3时,M点坐标 , N点坐标 ;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.27. 如图,平行四边形中, , .对角线 , 相交于点 , 将直线绕点顺时针旋转 , 分别交直线、于点、.
(1)、在t=3时,M点坐标 , N点坐标 ;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.27. 如图,平行四边形中, , .对角线 , 相交于点 , 将直线绕点顺时针旋转 , 分别交直线、于点、. (1)、当°,四边形是平行四边形;(2)、在旋转的过程中,从、、、、、中任意找4个点为顶点构造四边形.
(1)、当°,四边形是平行四边形;(2)、在旋转的过程中,从、、、、、中任意找4个点为顶点构造四边形.① ▲ °,构造的四边形是菱形;
②若构造的四边形是矩形,则不同的矩形应该有 ▲ 个.
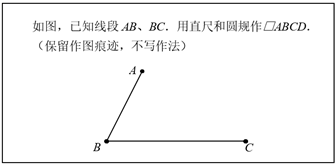
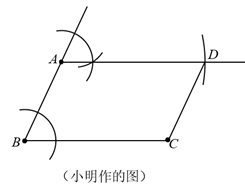
四、作图题(共2题,共11分)