苏科版数学八年级下学期复习微专题训练7 中心对称
试卷更新日期:2023-04-19 类型:复习试卷
一、单选题(每题2分,共16分)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形是中心对称图形但不是轴对称图形的是( )A、
2. 下列图形是中心对称图形但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列图案既是轴对称又是中心对称图形的有( )A、
3. 下列图案既是轴对称又是中心对称图形的有( )A、 B、
B、 C、
C、 D、
D、 4. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
4. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、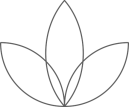 B、
B、 C、
C、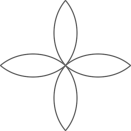 D、
D、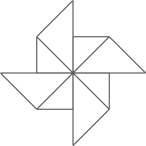 5. 江苏省第二十届运动会将于今年8月28日在泰州举行,运动会会徽依据“江苏•泰州”首字母为原型进行设计.下列字母中,是中心对称图形的有( )个.
5. 江苏省第二十届运动会将于今年8月28日在泰州举行,运动会会徽依据“江苏•泰州”首字母为原型进行设计.下列字母中,是中心对称图形的有( )个. A、1 B、2 C、3 D、46. 图①是苏州园林内的一种窗棂,图②是这种窗棂中的部分图案,该图案是由1个正六边形和6个全等的等边三角形组成的,则该图案( )
A、1 B、2 C、3 D、46. 图①是苏州园林内的一种窗棂,图②是这种窗棂中的部分图案,该图案是由1个正六边形和6个全等的等边三角形组成的,则该图案( ) A、既不是轴对称图形也不是中心对称图形 B、是中心对称图形但并不是轴对称图形 C、是轴对称图形但并不是中心对称图形 D、既是轴对称图形又是中心对称图形7. 下列说法正确的是( )A、想了解昆明市城镇居民人均年收入水平,应采用全面调查 B、要反映昆明市某周大气中的变化情况,宜采用扇形统计图 C、“某彩票中奖率为1%”可以理解为买张该彩票也可能中奖 D、画“任意一个矩形,是中心对称图形”,这一事件是随机事件8. 将一张正方形纸片,按如图①,②的步骤,沿虚线对折两次,然后沿图③中的虚线剪去一个角得到图④,将图④展开铺平后的图形( )
A、既不是轴对称图形也不是中心对称图形 B、是中心对称图形但并不是轴对称图形 C、是轴对称图形但并不是中心对称图形 D、既是轴对称图形又是中心对称图形7. 下列说法正确的是( )A、想了解昆明市城镇居民人均年收入水平,应采用全面调查 B、要反映昆明市某周大气中的变化情况,宜采用扇形统计图 C、“某彩票中奖率为1%”可以理解为买张该彩票也可能中奖 D、画“任意一个矩形,是中心对称图形”,这一事件是随机事件8. 将一张正方形纸片,按如图①,②的步骤,沿虚线对折两次,然后沿图③中的虚线剪去一个角得到图④,将图④展开铺平后的图形( ) A、是轴对称图形,但不是中心对称图形 B、是中心对称图形,但不是轴对称图形 C、不是轴对称图形,也不是中心对称图形 D、是中心对称图形,也是轴对称图形
A、是轴对称图形,但不是中心对称图形 B、是中心对称图形,但不是轴对称图形 C、不是轴对称图形,也不是中心对称图形 D、是中心对称图形,也是轴对称图形二、填空题(每空3分,共24分)
-
9. 已知点A(-1,2)与点B(3,4)是成中心对称的图形上的两个对称点,则对称中心的坐标为。10. 四张质地、大小、背面完全相同的卡片上,正面分别画有平行四边形、矩形、等腰三角形、菱形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为.11. 如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为.
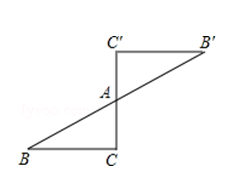 12. 如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转°后能与△DEF重合.
12. 如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转°后能与△DEF重合.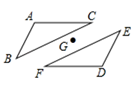 13. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成中心对称且也以格点为顶点的三角形共有个;(不包括本身)
13. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成中心对称且也以格点为顶点的三角形共有个;(不包括本身)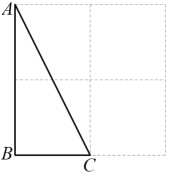 14. 如图,的对角线、交于点 , 则图中成中心对称的三角形共有对.
14. 如图,的对角线、交于点 , 则图中成中心对称的三角形共有对. 15. 如图, 和 关于点C成中心对称,若 , , ,则 的长是.
15. 如图, 和 关于点C成中心对称,若 , , ,则 的长是. 16. 如图,在平面直角坐标系中,点A,B,C的坐标分别为 , , . 点M从坐标原点O出发,第一次跳跃到点 , 使得点与点O关于点A成中心对称;第二次跳跃到点 , 使得点与点关于点B成中心对称;第三次跳跃到点 , 使得点与点关于点C成中心对称;第四次跳跃到点 , 使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
16. 如图,在平面直角坐标系中,点A,B,C的坐标分别为 , , . 点M从坐标原点O出发,第一次跳跃到点 , 使得点与点O关于点A成中心对称;第二次跳跃到点 , 使得点与点关于点B成中心对称;第三次跳跃到点 , 使得点与点关于点C成中心对称;第四次跳跃到点 , 使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .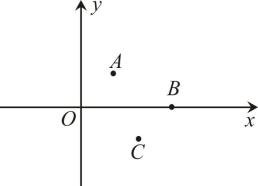
三、作图题(共6题,共50分)
-
17. 如图,已知△ABC的三个顶点坐标为A(3,4),B(2,0),C(8,0).
 (1)、请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标 ▲ ;(2)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.18. 图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,点A、B均在格点上,仅用无刻度的直尺在下列网格中按要求作图.
(1)、请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标 ▲ ;(2)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.18. 图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,点A、B均在格点上,仅用无刻度的直尺在下列网格中按要求作图.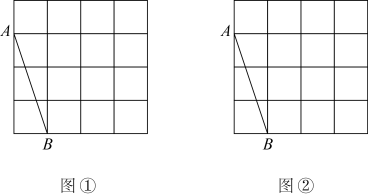 (1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.19. 如图,在平面直角坐标系中,已知点 , 轴于A.
(1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.19. 如图,在平面直角坐标系中,已知点 , 轴于A.
⑴画出将绕原点顺时针旋转后所得的 , 并写出点的坐标;
⑵画出关于原点O的中心对称图形 , 并写出点的坐标.
⑶画出向左平移2个单位后所得到的图形 , 求出线段划过的图形面积
20. 如图,在平面直角坐标系中,即△ABC的三个顶点分别是A(﹣3,2),B(﹣1,4),C(0,2). (1)、将△ABC以点O为旋转中心旋转180°,画出旋转后对应的△A1B1C1.(2)、平移△ABC,若点A的对应点A2的坐标为(﹣5,﹣2);则点B的对应点坐标是(3)、将△ABC以点O为旋转中心顺时针旋转90°,直接写出点A对应点的坐标(4)、若将△A1B1C1绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标为.21. 如图,在正方形网格中每个小正方形的边长都为1,每个正方形的顶点称为格点,的三个顶点A、B、C均在格点上.
(1)、将△ABC以点O为旋转中心旋转180°,画出旋转后对应的△A1B1C1.(2)、平移△ABC,若点A的对应点A2的坐标为(﹣5,﹣2);则点B的对应点坐标是(3)、将△ABC以点O为旋转中心顺时针旋转90°,直接写出点A对应点的坐标(4)、若将△A1B1C1绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标为.21. 如图,在正方形网格中每个小正方形的边长都为1,每个正方形的顶点称为格点,的三个顶点A、B、C均在格点上.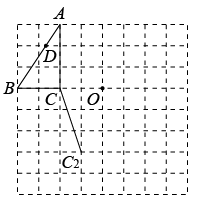 (1)、请在网格上作出关于点O成中心对称的 , A、B、C的对应点分别为、、(不写作法);(2)、把沿着方向平移得到 , 使A、B、C的对应点分别为、、 , 请在网格上作出(不写作法);(3)、如图,D为AB上一点,根据所作的图形,直接写出的面积为 .22. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)、请在网格上作出关于点O成中心对称的 , A、B、C的对应点分别为、、(不写作法);(2)、把沿着方向平移得到 , 使A、B、C的对应点分别为、、 , 请在网格上作出(不写作法);(3)、如图,D为AB上一点,根据所作的图形,直接写出的面积为 .22. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.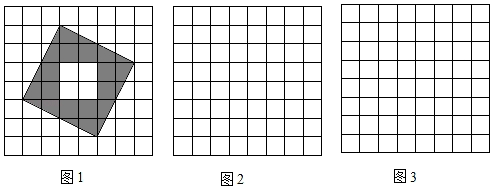 (1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
(1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
四、解答题(共3题,共30分)
-
23.
知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
 (1)、如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFBS四边形DEFC(填“>”“<”“=”);(2)、如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;(3)、八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分分割).24. 阅读与思考,请阅读下列材料,并完成相应的任务.
(1)、如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFBS四边形DEFC(填“>”“<”“=”);(2)、如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;(3)、八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分分割).24. 阅读与思考,请阅读下列材料,并完成相应的任务.旋转对称图形
观察右图中的正六边形,点O是它的内角平分线的交点,将这个正六边形绕着点O旋转 , 旋转后的图形与旋转前的图形重合.

一般地,如果把一个图形绕着某一点旋转一定角度(小于)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个点叫它的对称中心.
(1)、中心对称图形旋转对称图形.(填“是”或“不是”)(2)、下列图形中不是旋转对称图形的有 , 既是旋转对称图形又是中心对称图形的有 , 旋转72°能够完全重合的图形有 .A.
 B.
B. C.
C. D.
D. E.
E. 25. 规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.
25. 规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.
根据以上规定,回答问题:
(1)、下列图形是旋转对称图形,但不是中心对称图形的是________;A、矩形 B、正五边形 C、菱形 D、正六边形(2)、下列图形中,是旋转对称图形,且有一个旋转角是60度的有:(填序号);
 (3)、下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;A、0 B、1 C、2 D、3(4)、如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
(3)、下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;A、0 B、1 C、2 D、3(4)、如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.