苏科版数学八年级下学期复习微专题训练6 图形的旋转
试卷更新日期:2023-04-19 类型:复习试卷
一、单选题(每题2分,共16分)
-
1. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )
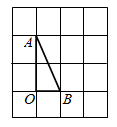 A、
A、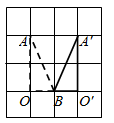 B、
B、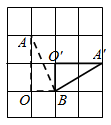 C、
C、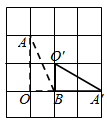 D、
D、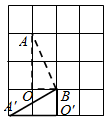 2. 如图,将△AOB绕点O按逆时针方向旋转60°后得到 , 若∠AOB=25°,则的度数是( )
2. 如图,将△AOB绕点O按逆时针方向旋转60°后得到 , 若∠AOB=25°,则的度数是( ) A、25° B、35° C、40° D、85°3. 如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连接CE,DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
A、25° B、35° C、40° D、85°3. 如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连接CE,DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )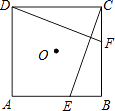 A、45° B、60° C、90° D、120°4. 如图,在正方形ABCD中, , E为AB边上一点,点F在BC边上,且 , 将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为( )
A、45° B、60° C、90° D、120°4. 如图,在正方形ABCD中, , E为AB边上一点,点F在BC边上,且 , 将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为( ) A、2 B、 C、3 D、5. 如图,在△ABC中,∠BAC=102°,将△ABC绕点A按逆时针方向旋转得到.若点恰好落在BC边上,且 , 则的度数为( )
A、2 B、 C、3 D、5. 如图,在△ABC中,∠BAC=102°,将△ABC绕点A按逆时针方向旋转得到.若点恰好落在BC边上,且 , 则的度数为( ) A、24° B、26° C、28° D、30°6. 如图,平面内三点A、B、C,AB=4 , AC= , 以BC为对角线作正方形BDCE,连接AD,则AD的最大值是( )
A、24° B、26° C、28° D、30°6. 如图,平面内三点A、B、C,AB=4 , AC= , 以BC为对角线作正方形BDCE,连接AD,则AD的最大值是( ) A、5 B、 C、7 D、77. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A、5 B、 C、7 D、77. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )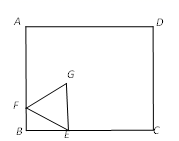 A、3 B、2.5 C、4 D、28. 如图,在正方形中,将边绕点B逆时针旋转至 , 连接 , , 若 , , 则线段的长度为( )
A、3 B、2.5 C、4 D、28. 如图,在正方形中,将边绕点B逆时针旋转至 , 连接 , , 若 , , 则线段的长度为( )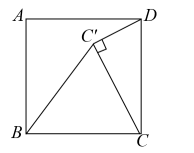 A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题(每空2分,共16分)
-
9. 要使正十二边形旋转后与自身重合,至少应将它绕中心旋转的度数为10. 荡秋千(填“属于”、“不属于”)旋转;11. 如图,在平面直角坐标系中,点C的坐标为(﹣1,0),点A的坐标为(﹣3,3),将点A绕点C顺时针旋转90°得到点B,则点B的坐标为.
 12. 如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠C′AB′的度数为 .
12. 如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠C′AB′的度数为 .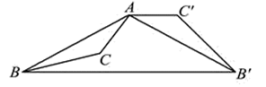 13. 如图,在平面直角坐标系中,已知菱形OABC的顶点O、B的坐标分别为(0,0)、(2,2),若菱形绕点O逆时针旋转135°时,菱形的对角线交点D的坐标为 .
13. 如图,在平面直角坐标系中,已知菱形OABC的顶点O、B的坐标分别为(0,0)、(2,2),若菱形绕点O逆时针旋转135°时,菱形的对角线交点D的坐标为 . 14. 如图,在矩形ABCD中,AC是对角线.将矩形ABCD绕点B顺时针旋转90°到矩形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为 .
14. 如图,在矩形ABCD中,AC是对角线.将矩形ABCD绕点B顺时针旋转90°到矩形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为 .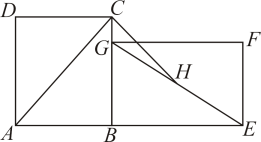 15. 如图, 中, , , ,且 边在直线 上,将 绕点A顺时针旋转到位置①可得到点 ,此时 ;将位置①的三角形绕点 顺时针旋转到位置②,可得到点 ,此时 ;将位置②的三角形绕点 顺时针旋转到位置③,可得到点 ,此时 ;…,其中 、 、 ……都在直线 上,按此规律继续旋转,直至得到点 为止,则 .
15. 如图, 中, , , ,且 边在直线 上,将 绕点A顺时针旋转到位置①可得到点 ,此时 ;将位置①的三角形绕点 顺时针旋转到位置②,可得到点 ,此时 ;将位置②的三角形绕点 顺时针旋转到位置③,可得到点 ,此时 ;…,其中 、 、 ……都在直线 上,按此规律继续旋转,直至得到点 为止,则 . 16. 如图,在矩形中, , , 连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形;再连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形 , …,按照此规律作下去.若矩形的面积记作 , 矩形的面积记作 , 矩形的面积记作 , …,则的值为 .
16. 如图,在矩形中, , , 连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形;再连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形 , …,按照此规律作下去.若矩形的面积记作 , 矩形的面积记作 , 矩形的面积记作 , …,则的值为 .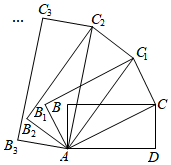
三、作图题(共3题,共21分)
-
17. 如图,在平面直角坐标系中,的三个顶点分别是 , , .
 (1)、将△ABC绕C点旋转180°,作出旋转后对应的△A1B1C1;(2)、平移△ABC到△A2B2C2 , 使点A的对应点A2的坐标为(﹣1,﹣4);(3)、若将△A1B1C1绕某一点旋转可以得到△A2B2C2 , 则该旋转中心的坐标为 .18. 如图,在平面直角坐标系xOy中,点A(2,0),B(5,0),C(4,2).
(1)、将△ABC绕C点旋转180°,作出旋转后对应的△A1B1C1;(2)、平移△ABC到△A2B2C2 , 使点A的对应点A2的坐标为(﹣1,﹣4);(3)、若将△A1B1C1绕某一点旋转可以得到△A2B2C2 , 则该旋转中心的坐标为 .18. 如图,在平面直角坐标系xOy中,点A(2,0),B(5,0),C(4,2).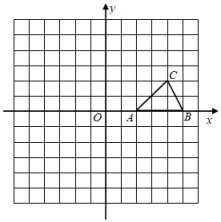 (1)、画出△ABC关于点O的中心对称图形,点A、B、C的对应点分别是D、E、F;(2)、若y轴上存在一点M,使得△MDF的周长最小,求点M的坐标.19. 如图,在正方形网格中,△AOB的顶点均在格点上点A、B的坐标分别是A(3,2)、B(1,3).
(1)、画出△ABC关于点O的中心对称图形,点A、B、C的对应点分别是D、E、F;(2)、若y轴上存在一点M,使得△MDF的周长最小,求点M的坐标.19. 如图,在正方形网格中,△AOB的顶点均在格点上点A、B的坐标分别是A(3,2)、B(1,3).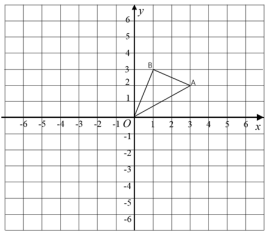 (1)、点A关于点O中心对称点的坐标为;(2)、△AOB绕点O顺时针旋转90°后得到△A1OB1 , 在方格纸中画出△A1OB1 , 并写出点B1的坐标 ▲ ;(3)、在y轴上找一点P,使得PA+PB最小,请在图中标出点P的位置,并求出这个最小值.
(1)、点A关于点O中心对称点的坐标为;(2)、△AOB绕点O顺时针旋转90°后得到△A1OB1 , 在方格纸中画出△A1OB1 , 并写出点B1的坐标 ▲ ;(3)、在y轴上找一点P,使得PA+PB最小,请在图中标出点P的位置,并求出这个最小值.四、解答题(共7题,共67分)
-
20. 如图,将矩形 绕点 顺时针旋转 得矩形 , 当点 落在 上时,连接 .求证: .
 21. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.(1)、如图1,当点E恰好在AC上时,求∠CDE的度数;
21. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.(1)、如图1,当点E恰好在AC上时,求∠CDE的度数;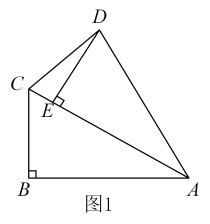 (2)、如图2,若=60° 时,点F是边AC中点,求证:四边形BFDE是平行四边形;
(2)、如图2,若=60° 时,点F是边AC中点,求证:四边形BFDE是平行四边形;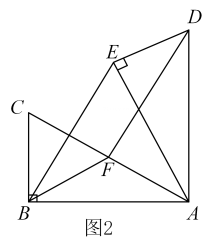 (3)、当BC=2时,连接CE,CD,设△CDE的面积为S.在旋转过程中,S是否存在最大值?若存在,请直接写出S的最大值;若不存在,请说明理由.22. 问题情境:
(3)、当BC=2时,连接CE,CD,设△CDE的面积为S.在旋转过程中,S是否存在最大值?若存在,请直接写出S的最大值;若不存在,请说明理由.22. 问题情境:如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE′(点A的对应点为点C).延长AE交CE′于点F,连接DE.
 (1)、猜想证明:
(1)、猜想证明:试判断四边形BE'FE的形状,并说明理由;
(2)、如图②,若DA=DE,请猜想线段CF与的数量关系并加以证明;(3)、解决问题:如图①,若AB=4,当BE的长为时,△ADE为等腰三角形,请直接写出结果.
23. 如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE. (1)、求证:DE⊥AG;(2)、正方形ABCD固定,将正方形OEFG绕点O逆时针旋转角(0°< <360°)得到正方形 , 如图2.
(1)、求证:DE⊥AG;(2)、正方形ABCD固定,将正方形OEFG绕点O逆时针旋转角(0°< <360°)得到正方形 , 如图2.①在旋转过程中,当∠是直角时,求的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
②若正方形ABCD的边长为1,在旋转过程中,求长的最大值和此时的度数,直接写出结果不必说明理由.
24. 已知:在边长为6的正方形ABCD中,点P为对角线BD上一点,且 . 将三角板的直角顶点与点P重合,一条直角边与直线BC交于点E,另一条直角边与射线BA交于点F(点F不与点B重合),将三角板绕点P旋转. (1)、如图,当点E、F在线段BC、AB上时,求证:PE=PF;(2)、当∠FPB=60°时,求△ BEP的面积;(3)、当△ BEP为等腰三角形时,直接写出线段BF的长.25. 如图,点E,F分别在正方形ABCD的边CD,BC上,且DE=CF,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转90得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
(1)、如图,当点E、F在线段BC、AB上时,求证:PE=PF;(2)、当∠FPB=60°时,求△ BEP的面积;(3)、当△ BEP为等腰三角形时,直接写出线段BF的长.25. 如图,点E,F分别在正方形ABCD的边CD,BC上,且DE=CF,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转90得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.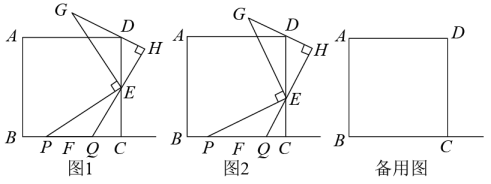 (1)、如图①,若点E是CD的中点,点P在线段BF上,则线段BP,QC,EC的数量关系为;(2)、如图②,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由;(3)、若正方形ABCD的边长为6,AB=3DE,CQ=1,请直接写出线段BP的长.26. 如图,正方形OABC中,O为坐标原点,点A、点C分别落在y轴、x轴上,点B坐标为(﹣4,4),点D为x轴上任意一点,将线段DA绕点D逆时针旋转90°,得对应线段为DE,作直线EC交y轴于点F.
(1)、如图①,若点E是CD的中点,点P在线段BF上,则线段BP,QC,EC的数量关系为;(2)、如图②,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由;(3)、若正方形ABCD的边长为6,AB=3DE,CQ=1,请直接写出线段BP的长.26. 如图,正方形OABC中,O为坐标原点,点A、点C分别落在y轴、x轴上,点B坐标为(﹣4,4),点D为x轴上任意一点,将线段DA绕点D逆时针旋转90°,得对应线段为DE,作直线EC交y轴于点F. (1)、如图(1),当点D为OC的中点时,求点E的坐标;(2)、如图(2),当点D在边OC上任意移动时,猜想:点F的位置是否发生变化?若不变,求出点F的坐标,若改变,请说明理由;(3)、如图(3),当点D在x轴的正半轴上移动时,请在图(3)画出图形(不保留作图痕迹),并直接回答点F的位置与(2)中猜想的结论是否一致.
(1)、如图(1),当点D为OC的中点时,求点E的坐标;(2)、如图(2),当点D在边OC上任意移动时,猜想:点F的位置是否发生变化?若不变,求出点F的坐标,若改变,请说明理由;(3)、如图(3),当点D在x轴的正半轴上移动时,请在图(3)画出图形(不保留作图痕迹),并直接回答点F的位置与(2)中猜想的结论是否一致.答:_(填“一致”或“不一致”).