苏科版数学八年级下学期复习微专题训练2 统计图表
试卷更新日期：2023-04-19 类型：复习试卷
一、单选题（每题2分，共12分）
-
1. 某校图书管理员清理课外书籍时，将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图，已知乙类书有90本，则丙类书的本数是（ ）
A、80 B、90 C、144 D、2002.某校对八年级300名学生就“分组合作学习”方式的支持程度进行了调查，随机抽取了若干名学生进行调查，并制作统计图，据此统计图估计该校八年级支持“分组合作学习”方式的学生（含非常喜欢和喜欢两种情况）约为（ ）
A、180名 B、210名 C、240名 D、270名3. 甲、乙两超市在1-5月间的盈利情况统计图如图所示，下列结论正确的是（ ）
A、甲超市的利润逐月减少 B、乙超市在6月份的利润必然超过甲超市 C、乙超市的利润逐月增加 D、3月份两家超市利润相同4. 如图为某队员射击10次的成绩统计图，该队员射击成绩的众数与中位数分别是（ ）
A、8，7 B、7，6.5 C、7，7 D、8，7.55. 宜兴市5月中旬每天平均空气质量指数(AQI)分别为84，89，83，99，69，73，78，81，89，82.为了八年级描述这十天空气质量的变化情况，最适合用的统计图是（ ）A、折线统计图 B、频数分布直方图 C、条形统计图 D、扇形统计图6. 牛奶中含有丰富的营养成分，其中水分约占82%，蛋白质约占4.3%，脂肪约占6%，乳糖约占7%，其他约占0.7%，对人体的健康有非常重要的作用．为直观地表示出各成分在总体中所占的百分比，最合适的统计图是（ ）
A、折线统计图 B、条形统计图 C、扇形统计图 D、频数分布直方图7. 下列说法正确的是（ ）A、想了解昆明市城镇居民人均年收入水平，应采用全面调查 B、要反映昆明市某周大气中的变化情况，宜采用扇形统计图 C、“某彩票中奖率为1%”可以理解为买张该彩票也可能中奖 D、画“任意一个矩形，是中心对称图形”，这一事件是随机事件8. 下列说法正确的是（ ）A、调查市场上某种白酒的塑化剂的含量，采用普查方式； B、要反映兴化市一周内每天的最高气温的变化情况，宜采用折线统计图； C、为了解一批电视机的使用寿命，任意抽取80台电视机进行试验，样本容量为80台； D、在一个透明的口袋中装有大小、外形一模一样的5个黄球，1个红球，摸出一个球是黄球是必然事件.二、填空题（每空2分，共14分）
-
9. 为了了解某校学生的视力情况，随机抽取了该校50名学生进行调查.整理样本数据如下表：
视力
4.7以下
4.7
4.8
4.9
4.9以上
人数
12
8
7
9
14
根据抽样调查结果，估计该校1 200名初中学生视力不低于4.8的人数是.
10. 扇形统计图中，某统计项目所对应的扇形的圆心角度数为72°，则该项目点总体的百分比为.11. 如图是某国产品牌手机专卖店去年 1 至 5 月高清大屏手机销售额折线统计图，根据图中信息，可以判断相邻两个月销售额变化最大的差的绝对值为万元.
12. 每年五月第三个星期日是全国助残日.在今年助残日前夕，某班进行了公益捐款活动，小明对本班同学的捐款情况进行了统计，绘制成如图所示的不完整的统计图，其中捐100元的人数占全班总人数的10%，由统计图可得全班同学平均每人捐款元.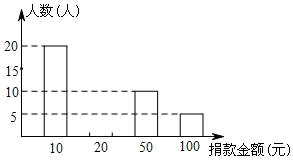
13. 如图所示是某中学七、八、九年级为贫困山区儿童捐款的统计图，已知该校七、八、九年级共有学生2000人，请根据统计图计算七、八、九年级共捐款元.
14. 疫情期间，某地为了描述每天新增“新冠肺炎”人数的变化过程和趋势，适合采统计图.15. 如图是当前对生活垃圾的常见三种处理方式，本图中的有关数据宜用统计图表示.
三、解答题（共10题，共90分）
-
16. 某地区为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费，为更好地决策，自来水公司随机抽取了部分用户的用水量数据，并绘制了不完整的统计图（每组数据包括右端点但不包括左端点），请你根据统计图解答下列问题：
(1)、此次抽样调查的样本容量是.(2)、补全频数分布直方图，扇形图中“15吨～20吨”部分的圆心角的度数＝ .(3)、如果自来水公司将基本用水量定为每户25吨，那么估计该地区10万用户中约有多少用户的用水全部享受基本价格？17. 某校为创建书香校园，倡导读书风尚，开展了师生“大阅读”活动，并制订“大阅读”星级评选方案（以整数评分），每月评选一次．为了了解活动开展情况，某星期学校组织对全校八年级“大阅读”五星级评选工作进行抽样调查，随机抽取20名学生阅读的积分情况进行分析：【收集数据】20名学生的“大阅读”积分如下（单位：分）：
32 43 34 35 15 46 48 24 45 10 25 40 60 42 55 30 47 28 37 42
【整理数据】
请你按如下表格分组整理、描述样本数据，并把下列表格补充完整．
积分/分
10≤x≤19
20≤x≤29
30≤x≤39
40≤x≤49
50≤x≤60
星级
红
橙
黄
绿
青
频数
2
3
5
m
n
根据以上数据可制成不完整的频数分布直方图．
(1)、填空：m＝ ， n＝；(2)、补全频数分布直方图；(3)、估计该校八年级600名学生中获得绿星级以上的人数．(4)、已知该校八年级学生小艺的积分为a分，是绿星级；小贤的积分为b分，是青星级．如果俩人的积分均未出现在样本中，那么b-a的最大值是 ．18. 每年6月14日是“世界献血日”，某地组织居民开展义务献血活动．参与的所有献血者的血型检测结果有“A”、“B”、“AB”、“O”4种血型．在所有参与献血者中，随机抽取了部分献血者的血型结果进行统计，并制作了两幅不完整的统计表．血型
A
B
AB
O
人数
a
10
5
b
(1)、这次随机抽取的献血者人数为人，m＝；(2)、上表中的a＝ ， b＝；(3)、若活动中该地有4000人参与义务献血，根据抽样结果回答：从所有献血者中任抽取一人，估计其血型是O型的概率是多少？并估计这4000人中大约有多少人是O型血？19. 2021年12月9日，神舟十三号乘组三位航天员首次在中国空间站进行太空授课，传播载人航天知识．某校为了了解本校学生对航天科技的关注程度，组织全校共600名学生进行了一次科普知识竞赛．为了了解本次竞赛学生的成绩分布情况，随机抽取了其中部分同学的成绩作为样本进行统计，将竞赛成绩（得分取整数）整理后分成四组，并制作了如下两个不完整的统计图，请根据所给信息，解答下列问题：
(1)、所抽取的学生数量为人，m＝；(2)、求成绩为这一组所在的扇形的圆心角度数；(3)、请补全频数直方图；(4)、若成绩不低于80分为“良好”等级，则全校参加这次竞赛的学生中属于“良好”等级的约有多少人？20. 我县教育部门为了解初中数学课堂中学生的参与情况，并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价.检测小组随机抽查部分学校若干名学生，并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图（均不完整）.请根据统计图中的信息解答下列问题：
(1)、①本次抽查的样本容量是 ，②补全条形统计图；
(2)、在扇形统计图中，“主动质疑”对应的圆心角度数为 ；(3)、如果该地区初中学生有10万名，那么在课堂上能独立思考的学生约有多少人？21. 学校为了解八年级学生体育测试成绩，以八年级（1）班学生的体育测试成绩为样本，按A，B，C，D四个等级进行统计（A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下），并将统计结果绘制成如下统计图，请你结合图中所给信息解答下列问题：
(1)、八年级（1）班学生的总人数是 ， m＝；(2)、把条形统计图补充完整；(3)、求八年级（1）班D等级所在扇形的圆心角度数.22. 4月23日是世界读书日，首届全民阅读大会在北京召开.为了积极响应世界读书日活动，某学校对本校学生课外阅读的情况作了抽样调查，从全体学生中随机抽取了部分学生进行调查，并将调查结果绘制成统计表.每周课外阅读时间（小时）
0～1
1～2（不含1）
2～3（不含2）
超过3
人数
7
10
14
19
每周课外阅读时间条形统计图
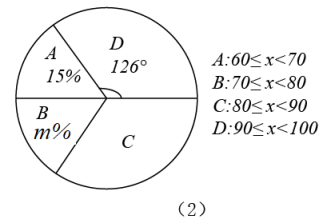
(1)、这次被调查的总人数是；(2)、已知该校全体学生人数为2000人，由此可以估计每周课外阅读时间超过3小时的学生有人；(3)、补全条形统计图；(4)、若用扇形统计图统计，那么表示第二小组[1～2（不含1）]的扇形圆心角度数是.23. 八（1）班学生参加了学校举行的“冬奥知识竞赛”活动，赛后老师对成绩进行分析，制作如下的频数分布表和扇形统计图：八（1）班学生冬奥知识竞赛成绩频数表
类别
分数段
频数（人数）
A
60≤x＜70
a
B
70≤x＜80
16
C
80≤x＜90
24
D
90≤x＜100
6
请根据以上统计图表解答下列问题：
(1)、八（1）班总数为；(2)、；(3)、扇形统计图中，类别B所在扇形的圆心角度数是°.(4)、全校共有720名学生参加比赛，若成绩在80分以上（含80分）为优秀，估计该校成绩优秀的学生有多少名？24. 中学生带手机上学的现象越来越受到社会的关注，为此某记者随机调查了某区若干名中学生家长对这种现象的态度（态度分为：A.无所谓；B.基本赞成；C.赞成：D.反对）.并将调查结果绘制成折线统计图1和扇形统计图2（不完整）.请根据图中提供的信息，解答下列问题.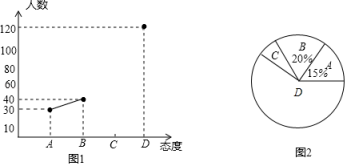
(1)、此次抽样调查中，共调查了名中学生家长；(2)、扇形统计图中，表示A类型的扇形圆心角的度数为.(3)、先求出C类型的人数，然后将图1中的折线图补充完整.(4)、根据抽样调查结果，请你估计该区18000名中学生家长中有多少名家长持反对态度？25. 今年3月22日“世界水日”，红星中学数学活动小组到某住宅区调查了解住宅区去年用水情况．该数学活动小组从住宅区中随机抽样调查了50个家庭去年每个月的用水情况，根据调查数据得到下面两张统计图：图1是去年50个家庭的月总用水量折线统计图，图2是去年50个家庭月总用水量的频数分布直方图（不完整）．请根据下面统计图，回答下面问题：
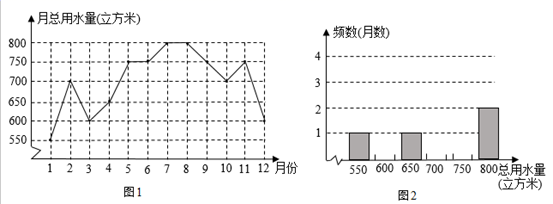(1)、根据图1的信息，补全频数分布直方图（图2）；(2)、去年50个家庭的月总用水量中，极差是立方米，中位数是立方米；(3)、根据上面数据，估计去年该住宅区每个家庭平均每月的用水量是多少立方米？