浙江省浙大附中丁兰校区2022-2023学年高二下学期数学期中试卷
试卷更新日期:2023-04-19 类型:期中考试
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 若复数z满足(i为虚数单位),则( )A、 B、1 C、 D、3. 已知单位向量满足 , 则在方向上的投影向量为( )A、 B、 C、 D、4. 已知直三棱柱的所有棱长都相等,M为的中点,则AM与所成角的正切值为( )A、 B、 C、 D、5. 已知为奇函数,为偶函数,若当时, , 则( )A、-1 B、0 C、1 D、26. 如图所示,一个球内接圆台,已知圆台上、下底面的半径分别为3和4,球的表面积为 , 则该圆台的体积为( )
 A、 B、 C、 D、7. 已知函数 , 则在区间上有且仅有个零点和条对称轴,则的取值范围是( )A、 B、 C、 D、8. , 则( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知函数 , 则在区间上有且仅有个零点和条对称轴,则的取值范围是( )A、 B、 C、 D、8. , 则( )A、 B、 C、 D、二、多选题
-
9. 已知 , 则( )A、 B、 C、 D、10. 已知直线与圆交于A、B两点,则下列说法正确的有( )A、直线l过定点 B、当取得最小值时, C、当取得最小值时,其余弦值为 D、的最大值为2411. 已知数列满足 , , 则下列说法正确的是( )A、 B、 C、 D、12. 如图,正方体的棱长为3,点是侧面上的一个动点(含边界),点在棱上,且 , 则下列结论正确的是( )
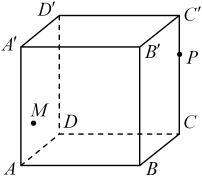 A、沿正方体的表面从点到点的最短路程为 B、平面 C、若保持 , 则点的运动轨迹长度为 D、三棱锥外接球的半径为
A、沿正方体的表面从点到点的最短路程为 B、平面 C、若保持 , 则点的运动轨迹长度为 D、三棱锥外接球的半径为三、填空题
-
13. 已知二项式的展开式所有项的系数之和为 , 则的展开式中的常数项为.14. 浙大附中高二年级某班元旦活动有唱歌、跳舞、小品、相声、朗诵、游戏六个节目制成一个节目单,其中游戏不安排在第一个,唱歌和跳舞相邻,则不同的节目单顺序有种(结果用数字作答)15. 已知椭圆的左、右焦点分别为 , 且是抛物线的焦点,若P是椭圆与抛物线的交点,且 , 则的值为.16. 若直线与曲线相切,直线与曲线相切,则的值为.
四、解答题
-
17. 如图,在平面四边形ABCD中,.
 (1)、当时,求的面积.(2)、当时,求.18. 已知数列的前n项和为 , 且.(1)、求数列的通项公式;(2)、在和之间插入n个数,使得这数依次组成公差为的等差数列,求数列的前n项和.19. 已知函数满足 .(1)、求函数的解析式;(2)、若关于x的方程恰有四个不同的实根,求实数k的取值范围.
(1)、当时,求的面积.(2)、当时,求.18. 已知数列的前n项和为 , 且.(1)、求数列的通项公式;(2)、在和之间插入n个数,使得这数依次组成公差为的等差数列,求数列的前n项和.19. 已知函数满足 .(1)、求函数的解析式;(2)、若关于x的方程恰有四个不同的实根,求实数k的取值范围.
