陕西省渭南市韩城市2022-2023学年七年级下学期数学期中调研试题

试卷更新日期：2023-04-19 类型：期中考试

进入出卷网下载

一、选择题(共8小题，每小题3分，计24分。)

1. 下列各数中，是无理数的是（）

A、 $- \frac{1}{3}$ B、2 C、 $\sqrt{7}$ D、0.0101

查看试题解析
2. 点(2，-3)在平面直角坐标系中所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，∠1和∠2是同位角的是（）.

A、 B、 C、 D、

查看试题解析
4. 能说明命题“对于任何实数a，都有|a|=a"是假命题的反例是（）

A、a=-2 B、a= $\frac{1}{2}$ C、a=1 D、a= $\sqrt{5}$

查看试题解析
5. 下列等式成立的是（）

A、 $\sqrt{49}$ =±7 B、 $\sqrt{(- 7)^{2}}$ =-7． C、( $^{3} \sqrt{- 7}$ )³=-7 D、( $- \sqrt{7}$ )²=-7

查看试题解析
6. 已知直线m∥n，将一块含30°角的直角三角板ABC(∠BAC=30°)，按如图所示方式放置，其中A、B两点分别落在直线m、n上，若∠1=35°，则∠2的度数是（）

A、25° B、30° C、35° D、45

查看试题解析
7. 已知甲、乙两个立方体，甲的体积是乙体积的8倍，则甲的棱长是乙的棱长的（）

A、8倍 B、2倍 C、4倍 D、 $\frac{1}{2}$ 倍

查看试题解析
8. 如图所示，以下5个条件：①∠B=∠4+∠5；②∠2=∠4；③∠1=∠5；④∠B=∠3；⑤∠D+∠4+∠5= 180°．其中一定能判定AD∥BC的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题(共5小题，每小题3分，计15分)

9. 比较大小： $- \sqrt{17}$ -4．(填“>"“<"或“=")

查看试题解析
10. 在平面直角坐标系中，将点A(-3，2)向上平移2个单位长度得到点B，则点B的坐标是

查看试题解析
11. 命题“平行于同一条直线的两条直线平行”的题设是，结论是这两条直线平行。

查看试题解析
12. 如图，将三角形ABC沿BC方向平移2 cm得到三角形DEF，若三角形ABC的周长等于10cm，则四边形ABFD的周长等于cm．

查看试题解析
13. 如图，长方形纸片ABCD，M为AD边上一点，将纸片沿BM、CM折叠，使A点落在A1处，D点落在D1处，若∠AMB=35°，∠1=40°，则∠MCB的度数为°

查看试题解析

三、解答题(共13小题，计81分。)

14. 计算： $\sqrt{4} +^{3} \sqrt{- 27} + | 1 - \sqrt{25} |$

查看试题解析
15. 已知平面直角坐标系中有一点M(m-1，2m+3)．若点M在x轴上，求M的坐标

查看试题解析
16. 如图，已知直线AB，CD相交于点O，∠COE=90°．

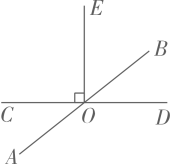(1)、写出∠BOD的对顶角和余角

(2)、若∠AOC=35°，求∠BOE的度数．

查看试题解析
17. 在如图所示的数轴上近似地表示下列各数，并用“<”连接．
$\frac{8}{3}$ ， 1.5， $- \sqrt{3}$ ， -π．

查看试题解析
18. 求下列各式中x的值：

(1)、4x²-36=0；

(2)、(x-1)³=8．

查看试题解析
19. 如图，BA平分∠EBC，CD平分∠ACF，且AB∥CD．试判断AC与BE的位置关系，并说明理由．

查看试题解析
20. 将半径为12 cm的实心铁球熔化，重新铸造出8个半径相同的实心小铁球，不计损耗，小铁球的半径是多少？(球的体积公式V= $\frac{4}{3}$ πR³ ，其中R是球的半径)

查看试题解析
21. 如图是某市火车站及周围的平面示意图，已知超市的坐标是(-2，4)，市场的坐标是(1，3)．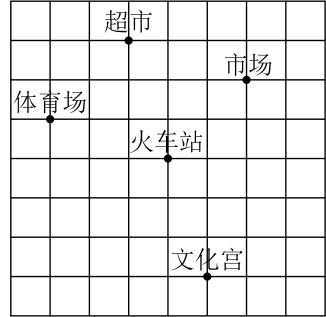

(1)、根据题意，画出相应的平面直角坐标系，并在图中标出汽车站(-3，-2)，花坛(2，-1)的位置；

(2)、分别写出体育场、火车站和文化官的坐标．

查看试题解析
22. 如图，AB⊥AC，点D、E分别在线段AC、BF上，DF、CE分别与AB交于点M、N，若∠1=∠2，∠C=∠F，求证；AB⊥BF．请完善解答过程，并在括号内填写相应的依据．

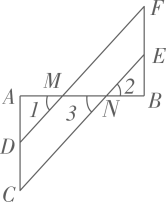
证明：∵∠1=∠2，∠2=∠3，

∴∠1=∠      ▲ ． (等量代换)

∴DF∥CE（）

∴∠ADM=∠      ▲ (两直线平行，同位角相等)

∵∠C=∠F，(已知)

∴∠ADM=∠      ▲ (等量代换)

∴AC∥BF（）

∴∠A=∠B（）

∵AB⊥AC，(已知)

∴∠A=90°．

∴∠B=90°．

∴AB⊥BF．（）

查看试题解析
23. 如图，若三角形A，B，C是由三角形ABC平移后得到的(A、B、C的对应点分别为A₁、B₁、C₁)，且三角形ABC中任意一点P(x，y)经过平移后的对应点为P₁(x-5，y+2)．

(1)、在图中画出三角形A₁B₁C₁；

(2)、求三角形ABC的面积．

查看试题解析
24. 如图，直线CD、EF交于点O，OA，OB分别平分∠COE和∠DOE，且∠1+∠2=90°．

(1)、求证：AB∥CD；

(2)、若∠2：∠3=25，求∠BOF的度数

查看试题解析
25. 我们知道， $\sqrt{2}$ 是一个无理数，将这个数减去整数部分，差就是小数部分．即 $\sqrt{2}$ 的整数部分是1，小数部分是 $\sqrt{2}$ -1，请回答以下问题：

(1)、 $\sqrt{10}$ 的小数部分是

(2)、若a是 $\sqrt{90}$ 的整数部分，b是 $\sqrt{3}$ 的小数部分求a+b- $\sqrt{3}$ +1的平方根；

(3)、若7+ $\sqrt{5}$ =x+y，其中x是整数，且0<y<1，求x-y+ $\sqrt{5}$ 的值

查看试题解析
26. 已知点E在直线AB，CD之间，且∠BAE=∠AEC-∠ECD．

(1)、如图1，求证：AB∥CD；

(2)、若AH平分∠BAE，FG∥CE．
①如图2，若∠AEC=98°，FH平分∠DFC，求∠AHF的度数；

②如图3，若FH平分∠CFC，试判断∠AHF与∠AEC的数量关系并说明理由．

查看试题解析