浙江省宁波市南三县2023年中考数学一模试题
试卷更新日期:2023-04-19 类型:中考模拟
一、选择题(每小题4分,共40分.)
-
1. -2023的绝对值是( )A、2023 B、-2023 C、 D、2. 下列计算正确的是( )A、4a-2a=2 B、 C、 D、3. 中华人民共和国第十四届人民代表大会第一次会议政府工作报告指出:2023年国内生产总值预期增长目标5%左右,城镇新增就业1200万人左右,将1200万用科学记数法表示为( )A、 B、 C、 D、4. 如图是一个底面为正三角形的直三棱柱,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 据调查,某班40名学生所穿鞋子鞋号统计如下表:
5. 据调查,某班40名学生所穿鞋子鞋号统计如下表:鞋号
20
21
22
23
24
频数
2
8
9
19
2
则该班学生所穿鞋子鞋号的中位数和众数分别是( )
A、23,22 B、22,23 C、17,23 D、23,236. 如图,在中, , D、E分别是AB、AC的中点,连结DE、CD。若 , , 则CD的长为( )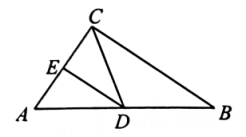 A、7 B、6 C、5 D、4.87. 小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原来的速度返回,父亲在报亭看报10分钟,然后用15分钟返回家,下面给出的图象中表示父亲离家距离与离家时间的函数关系是( )A、
A、7 B、6 C、5 D、4.87. 小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原来的速度返回,父亲在报亭看报10分钟,然后用15分钟返回家,下面给出的图象中表示父亲离家距离与离家时间的函数关系是( )A、 B、
B、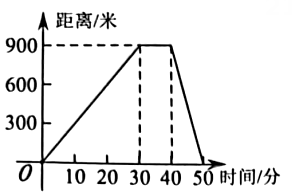 C、
C、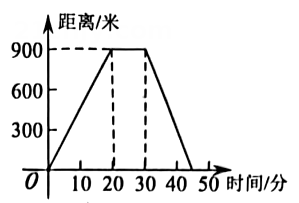 D、
D、 8. 我国古代数学名著《张丘建算经》中记载:“今有甲、乙怀钱,各不知其数,甲得乙十钱多乙余钱五倍,乙得甲十钱适等,问甲、乙怀钱各几何?”译文为:现有甲、乙两人带有一些银子,都不知道数量,甲得到乙的10两银子,甲比乙多出的银子是乙的5倍,乙得到甲的10两银子,两人的银子恰好相等,问甲、乙各带了多少两银子?设甲带了x两银子,乙带了y两银子,那么可列方程组为( )A、 B、 C、 D、9. 如图,一次函数的图象与反比例函数的图象交于点 , , 当时,x的取值范围是( )
8. 我国古代数学名著《张丘建算经》中记载:“今有甲、乙怀钱,各不知其数,甲得乙十钱多乙余钱五倍,乙得甲十钱适等,问甲、乙怀钱各几何?”译文为:现有甲、乙两人带有一些银子,都不知道数量,甲得到乙的10两银子,甲比乙多出的银子是乙的5倍,乙得到甲的10两银子,两人的银子恰好相等,问甲、乙各带了多少两银子?设甲带了x两银子,乙带了y两银子,那么可列方程组为( )A、 B、 C、 D、9. 如图,一次函数的图象与反比例函数的图象交于点 , , 当时,x的取值范围是( ) A、x<-1或x>2 B、x<-1或0<x<2 C、-1<x<0或0<x<2 D、-1<x<0或x>210. 如图,过的对称中心O的线段EF交AD于点E,交BC于点F,P为边AB上的一点,作交EF于Q,连结DQ,DF,PF,则只需要知道下列哪个图形的面积,就能知道的面积( )
A、x<-1或x>2 B、x<-1或0<x<2 C、-1<x<0或0<x<2 D、-1<x<0或x>210. 如图,过的对称中心O的线段EF交AD于点E,交BC于点F,P为边AB上的一点,作交EF于Q,连结DQ,DF,PF,则只需要知道下列哪个图形的面积,就能知道的面积( )
 A、的面积 B、的面积 C、的面积 D、四边形APQE的面积
A、的面积 B、的面积 C、的面积 D、四边形APQE的面积二、填空题(每小题5分,共30分)
-
11. 实数-27的立方根是12. 分解因式:13. 一个不透明的袋子里装有8个只有颜色不同的球,其中1个白球,2个红球,5个黄球,从布袋里任意摸出1个球,是黄球的概率为。14. 传统服饰日益受到关注,如图1为明清时期女子主要裙式之一的马面裙,如图2马面裙可以近似地看作扇环,其中AD长度为气米,BC长度为米,圆心角 , 则裙长AB为米。
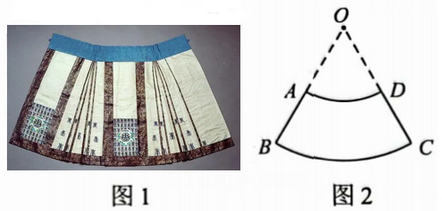 15. 如图,在中, , , , O为边AC上的动点,⊙O与AB边相切于点D,连结CD,当为直角三角形时,⊙O的半径为。
15. 如图,在中, , , , O为边AC上的动点,⊙O与AB边相切于点D,连结CD,当为直角三角形时,⊙O的半径为。 16. 如图,矩形OABC的顶点A、C分别在x轴和y轴上,反比例函数过BC的中点D。交AB于点E,F为AB上的一点,BF=2AF,过点F的双曲线交OD于点P,交OE于点Q,连结PQ,则k的值为 , 的面积为。
16. 如图,矩形OABC的顶点A、C分别在x轴和y轴上,反比例函数过BC的中点D。交AB于点E,F为AB上的一点,BF=2AF,过点F的双曲线交OD于点P,交OE于点Q,连结PQ,则k的值为 , 的面积为。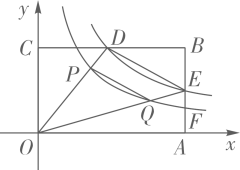
三、解答题(本大题有8小题,共80分)
-
17.(1)、计算:(2)、解不等式组:18. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点.的顶点均在格点上,分别按要求画出图形。
 (1)、将图1中的绕点A逆时针旋转90°,画出旋转后的。(2)、在图2中的BC上找一点F,使的面积与的面积之比为1:2。19. 为深入学习贯彻习近平法治思想,推动青少年宪法学习宣传教育走深走实,教育部组织开展第七届全国学生“学宪法讲宪法”系列活动,某校积极响应教育部的号召,开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动,下表是参加冠亚军决赛的两名选手的各项测试成绩(单位:分)。(1)、若将在线学习、知识竞赛与演讲比赛三项成绩的平均分作为最后成绩,谁将会获得冠军?(2)、若将在线学习、知识竞赛与演讲比赛的成绩按2:3:5的比例计算最后成绩,谁将会获得冠军?
(1)、将图1中的绕点A逆时针旋转90°,画出旋转后的。(2)、在图2中的BC上找一点F,使的面积与的面积之比为1:2。19. 为深入学习贯彻习近平法治思想,推动青少年宪法学习宣传教育走深走实,教育部组织开展第七届全国学生“学宪法讲宪法”系列活动,某校积极响应教育部的号召,开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动,下表是参加冠亚军决赛的两名选手的各项测试成绩(单位:分)。(1)、若将在线学习、知识竞赛与演讲比赛三项成绩的平均分作为最后成绩,谁将会获得冠军?(2)、若将在线学习、知识竞赛与演讲比赛的成绩按2:3:5的比例计算最后成绩,谁将会获得冠军?选手
项目
在线学习
知识竞赛
演讲比赛
甲
84
96
90
乙
89
99
85
20. 如图,已知二次函数的图象经过点 , 点。 (1)、求二次函数的表达式和顶点坐标。(2)、点在该二次函数图象上,当时,求n的值。(3)、已知 , , 若将该二次函数的图象向上平移k(k>0)个单位后与线段AB有交点,请结合图象,直接写出k的取值范围。21. 如图1是一架踏板式人字梯,如图2是其侧面结构示意图,左支撑架AB和右支撑架AC长度都为100cm,最上一层的踏板侧面DE平行于地面BC, , 若支撑架的张角。
(1)、求二次函数的表达式和顶点坐标。(2)、点在该二次函数图象上,当时,求n的值。(3)、已知 , , 若将该二次函数的图象向上平移k(k>0)个单位后与线段AB有交点,请结合图象,直接写出k的取值范围。21. 如图1是一架踏板式人字梯,如图2是其侧面结构示意图,左支撑架AB和右支撑架AC长度都为100cm,最上一层的踏板侧面DE平行于地面BC, , 若支撑架的张角。
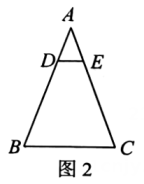 (1)、求BC的长。(2)、求踏板DE到地面的距离(结果精确到1cm)(参考数据:sin20°≈0.34,cos20°≈0.94,tan°80≈0.36)22. 抗击疫情期间,某商店购进了一种消毒用品,进价为每件8元,销售过程中发现,该商品每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数),部分对应值如下表:
(1)、求BC的长。(2)、求踏板DE到地面的距离(结果精确到1cm)(参考数据:sin20°≈0.34,cos20°≈0.94,tan°80≈0.36)22. 抗击疫情期间,某商店购进了一种消毒用品,进价为每件8元,销售过程中发现,该商品每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数),部分对应值如下表:每件售价(元)
9
11
13
每天的销售量(件)
105
95
85
(1)、求y与x的函数关系式。(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元。(3)、设该商店销售这种消毒用品每天获利w(元),问:当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?23. 如图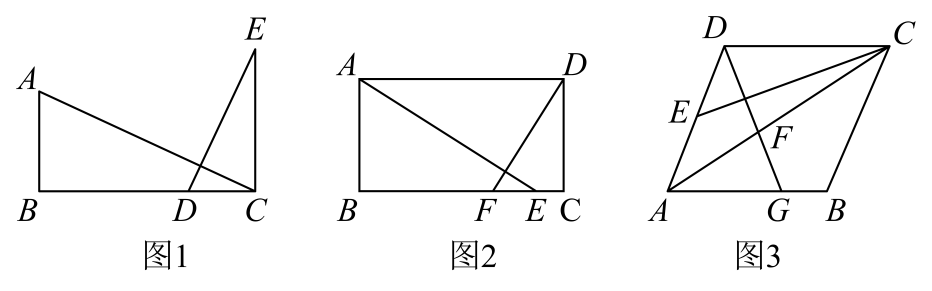 (1)、【基础巩固】
(1)、【基础巩固】
如图1,于点B,于点C,交BC于点D,求证:。(2)、【尝试应用】
如图2,在矩形ABCD中,E是BC上的一点,作交BC于点F, , 若 , , 求的值。(3)、【拓展提高】
如图,菱形ABCD的边长为10, , E为AD上的一点,作交AC于点F,交AB于点G,且 , 求BG的长。24. 如图1,AC为的对角线,的外接圆⊙O交CD于点E,连结BE。 (1)、求证:。(2)、如图2,当时,连结OA、OB,延长AO交BE于点G,求证。(3)、如图3,在(2)的条件下,记AC、BE的交点为点F,连结AE、OF。
(1)、求证:。(2)、如图2,当时,连结OA、OB,延长AO交BE于点G,求证。(3)、如图3,在(2)的条件下,记AC、BE的交点为点F,连结AE、OF。①求证:。
②当时,求的值。