浙江省温州市瓯海区某校2022-2023学年七年级下学期期中检测数学试题

试卷更新日期：2023-04-19 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 如图，在所标识的角中，内错角是（）．

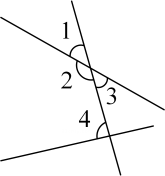A、∠1与∠4 B、∠2与∠4 C、∠3与∠4 D、∠1与∠3

查看试题解析
2. 据最新消息，华为在3nm芯片研发中已经取得可喜成绩，保持世界领先的研发水平!请用科学记数法表示3nm为（）．(1nm=0.0000001cm)

A、3×10^-7cm B、3×10^-6cm C、3×10^-5cm D、0.3×10^-6cm

查看试题解析
3. 下列各组数中，是二元一次方程5x-y=2的一个解的是（）．

A、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 0 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$

查看试题解析
4. 下列运算正确的是（）．

A、a²＋a⁴＝a⁶ B、(a－b)²＝a²－b² C、(a²b)³＝a⁶b³ D、a⁶÷a⁶＝a

查看试题解析
5. 已知二元一次方程组 ${\begin{array}{l} m + 2 n = 8 ① \\ 2 m - 3 n = 2 ② \end{array}$ ，如果①×2-②，那么所得的方程是（）．

A、n=14 B、7n=14 C、5n=6 D、7n=6

查看试题解析
6. 计算(-6x-5y)(5y-6x)的结果是（）．

A、 $36 x^{2} - 25 y^{2}$ B、 $25 y^{2} - 36 x^{2}$ C、 $- 36 x^{2} - 25 y^{2}$ D、 $36 x^{2} + 25 y^{2}$

查看试题解析
7. 计算 $(- x^{5} + 3 x^{3} - M) \div (- 3 x) = \frac{1}{3} x^{4} - x^{2} + 2 x$ ，那么M=（）．

A、-3x B、 $3 x^{2}$ C、 $6 x^{2}$ D、 $- 6 x^{2}$

查看试题解析
8. 利用透镜我们可以聚合或分散光线，它被广泛应用于显微设备、射电天文、汽车雷达等领域，如图经过透镜后的光线互相平行，已知∠A=164°，∠C=171°，则∠AOC=（）

A、20° B、25° C、30° D、35°

查看试题解析
9. 《九章算术》中记载：“今有人共买物，人出八盈三；人出七不足四。问人数、物价各几何？”其大意是“现在有几个人共同买一件物品，若每人出8钱就多出3钱，若每人出7钱就差4钱，问人数、物品价格各是多少？”设人数为x人，物品价格为y钱，根据题意可列方程组方程组为（）．

A、 ${\begin{array}{l} y = 8 x + 3 \\ y = 7 x - 4 \end{array}$ B、 ${\begin{array}{l} y = 8 x - 3 \\ y = 7 x - 4 \end{array}$ C、 ${\begin{array}{l} y = 8 x + 3 \\ y = 7 x + 4 \end{array}$ D、 ${\begin{array}{l} y = 8 x - 3 \\ y = 7 x + 4 \end{array}$

查看试题解析
10. 如图，长方形纸片ABCD分别沿着EF、DH折叠后，点A，B，C分别落在点A′，B′，C′的位置，当DA'∥B'C'时，∠1=67°，则∠2=（）．

A、23° B、46° C、56° D、67°

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分）

11. 已知3x-y=7，请用x的代数式表示y，则y= ．

查看试题解析
12. 若 $3^{x} = 7 ， 3^{y} = 2$ ，则 $3^{x + 2 y}$ = ．

查看试题解析
13. 如图，∠BDC=90°，添加一个条件：，可使AB∥CD．

查看试题解析
14. 已知关于x，y的方程组 ${\begin{array}{l} 3 x - 2 y = 2 k \\ - 2 x + 3 y = 3 k \end{array}$ 满足x-y=1，则k的值为．

查看试题解析
15. 若x²+kx+9是完全平方式，则k= ．

查看试题解析
16. 一架满载的波音客机，如果紧急着陆，从飞机接触跑道开始，飞机的速度v和时间t之间符合v=v₀+at(v₀ ， a为常数)，当t=0s时，v=60m/s，当t=4s时v=36m/s，则a= ．

查看试题解析
17. 如图，5张长为a，宽为b(a>b)的小长方形纸片，不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示。设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，S始终保持不变，则a，b满足的关系是．

查看试题解析
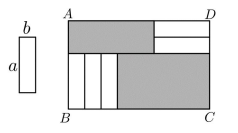18. 随着科技的发展，人们使用平板学习已经成为常态，它拥有的智能磁吸键盘和手写笔更是给人们带来无纸化学习新体验，如图1，当平板放在智能磁吸键盘上时，可调整平板角度，研究表明，屏幕中心在直视屏幕视线下方10°：20°时可减少视觉和肌肉骨骼不适．图2为调整示意图，即∠G=90°，∠GED=x°(10°<x<20°)时为最佳．当平板下沿落在第一个卡槽A时，键盘盖下半部分OC与键盘OP的夹角∠2=67°，键盘盖上、下半部分CD与OC的夹角∠3=134°，水平视线与屏幕视线夹角∠FED=38°，则x=；当平板下沿落在卡槽B时，∠2=53°，∠3=106°，则∠FED= ．

查看试题解析

三、解答题（本题有6小题，共46分）

19.

(1)、计算： $(- 2)^{2} - 202 3^{0} + {(\frac{1}{2})}^{- 3}$

(2)、化简：(2x-y)(2x+y)-(2x-y)²

查看试题解析
20. 已知 $\sqrt{3 a + 2 b + 1} + (5 a - 4 b + 9)^{2} = 0$ ，求 $a^{2} + b^{2}$ 的值．

查看试题解析
21. 在正方形网格中，每个小正方形的边长均为1个单位长度，三角形ABC如图所示．现将三角形ABC向右平移2个单位长度，得到三角形A₁B₁C₁ ．

(1)、请画出平移后的三角形A₁B₁C₁ ．

(2)、经过平移后，线段A₁B₁与BC的交点是点O，则四边形COB₁C₁的面积是．

查看试题解析
22. 如图，已知∠ABC+∠DCB=180°且∠1=∠2，试说明∠GFA+∠FDB=180°，请将下面的说明过程填写完整．

解：∵∠ABC+∠DCB=180°

∴CG∥AB，

∴∠1=∠FEA，（      ）

∵∠1=∠2，∴∠2=∠FEA，（      ）

∴EG∥      ▲ ，（      ）

∴      ▲ +∠FDB=180°，

∵∠GFA=∠DFE，（      ）

∴∠GFA+∠FDB=180°．

查看试题解析
23. 同学们一起布置艺术节活动现场，现在有一个边长为a的大正方形固定场地，以及四个边长为b的小正方形活动场地，设计如图1所示的阴影部分为展览区，其面积为S₁；如图2所示的阴影部分为竞赛区，其面积为S₂ ．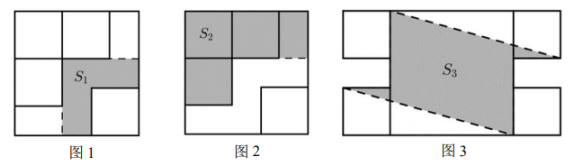

(1)、用含a，b的代数式分别表示S₁、S₂ ．

(2)、若a+b＝17，a²+b²=169，求S₁+S₂的值．

(3)、如图3，在（2）的基础上，将四个活动区域外移，形成的阴影部分为表演场地，其面积为S₃ ，求S₃的值．

查看试题解析

24. 在我校“英语节”活动中为表彰先进，现计划购买A，B，C三种类型的奖品（每种类型至少1件）作为鼓励，要求C类型奖品件数是A类型奖品件数的2倍，三种类型奖品的单价如下表：

类型	A	B	C
单价（元/件）	30	25	20

设购进x件A类型奖品，y件B类型奖品．

(1)、根据信息填表：

	A	B	C
数量（件）	x	y	2x
费用（元）	30x	▲	▲

(2)、根据信息解答问题：

①若购买三种类型的奖品总数为100件，共花费2400元，则三种类型的奖品分别购进多少件？

②为节省开支，若购买三种类型的奖品共花费2000元，且B种类型的奖品件数超过总奖品件数的一半，则三种类型的奖品总数为多少件？

查看试题解析