浙江省嘉兴市上外秀洲2023年第二次校级中考模拟数学试题
试卷更新日期:2023-04-19 类型:中考模拟
一、单选题
-
1. 计算: 的结果是( )A、-5 B、-1 C、1 D、52. 为了了解家里的用水情况,以便能更好地节约用水,小方把自己家1至6月份的用水量绘制成折线图,那么小方家这6个月的月用水量最大的是( )
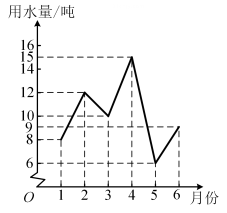 A、1月 B、2月 C、4月 D、6月3. 如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( )
A、1月 B、2月 C、4月 D、6月3. 如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 不等式组 的解是( )A、 B、 C、 D、6. 若关于 的一元二次方程 有两个相等实数根,则 的值是( )A、-1 B、1 C、-4 D、47. 某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如下表
4. 下列计算正确的是( )A、 B、 C、 D、5. 不等式组 的解是( )A、 B、 C、 D、6. 若关于 的一元二次方程 有两个相等实数根,则 的值是( )A、-1 B、1 C、-4 D、47. 某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如下表人数(人)
1
3
4
1
分数(分)
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是( )
A、90,90 B、90,85 C、90,87.5 D、85,858. 如图,在 中, , ,D在 上,且 ,则 的长是( ) A、2 B、 C、 D、9. 如图,在△ABC中,∠C=2∠B,分别以点A、B为圆心,大于 AB的长为半径画弧,两弧交于点M、N,作直线MN,交BC边于点D,连接AD,若AD=5,CD=6,则AB的长是( )
A、2 B、 C、 D、9. 如图,在△ABC中,∠C=2∠B,分别以点A、B为圆心,大于 AB的长为半径画弧,两弧交于点M、N,作直线MN,交BC边于点D,连接AD,若AD=5,CD=6,则AB的长是( ) A、5 B、8 C、4 D、1010. 如图, 经过 的顶点C,与边 分别交于点M,N,与 边相切.若 ,则线段 长度的最小值是( )
A、5 B、8 C、4 D、1010. 如图, 经过 的顶点C,与边 分别交于点M,N,与 边相切.若 ,则线段 长度的最小值是( )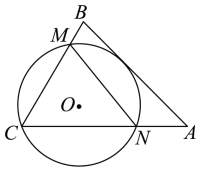 A、3 B、2 C、2 D、
A、3 B、2 C、2 D、二、填空题
-
11. 分解因式: = .12. 若分式 的值为0,则x的值是.13. 一个不透明的袋中,装有5个黄球,8个红球,7个白球,它们除颜色外都相同.从袋中任意摸出一个球,是黄球的概率是.14. 如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为.
 15. 如图,△ABC的顶点在正方形网格的格点上,则sinA的值为.
15. 如图,△ABC的顶点在正方形网格的格点上,则sinA的值为.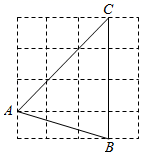 16. 如图,在平面直角坐标系中, , ,P是x轴上动点,连结 ,将线段 绕点A逆时针旋转 得到线段 ,连结 ,取 中点为M. 的度数为 , 的最小值为.
16. 如图,在平面直角坐标系中, , ,P是x轴上动点,连结 ,将线段 绕点A逆时针旋转 得到线段 ,连结 ,取 中点为M. 的度数为 , 的最小值为.
三、解答题
-
17.(1)、计算: .(2)、化简: .18. 如图(1),在方格纸中,每个小正方形边长都是1, 的四个顶点都在小方格的顶点上,按下列要求画一个面积与 面积相等的四边形,使他的顶点均在方格的顶点上.(四边形的边用实线表示,顶点写上规定的字母)
 (1)、在图(2)中画一个矩形 .(2)、在图(3)中画一个菱形 .19. 如图, 、 相交于点O, , .
(1)、在图(2)中画一个矩形 .(2)、在图(3)中画一个菱形 .19. 如图, 、 相交于点O, , . (1)、求证: .(2)、若 ,求 的度数.20. 为了解学生每周课外体育活动时间的情况,某学校随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在 小时的学生人数占 .根据以上信息及统计图解答下列问题:
(1)、求证: .(2)、若 ,求 的度数.20. 为了解学生每周课外体育活动时间的情况,某学校随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在 小时的学生人数占 .根据以上信息及统计图解答下列问题: (1)、请补全条形统计图;(2)、求这50名学生每周课外体育活动时间的平均数;(3)、已知该校共有1200名学生,请估计每周课外体育活动时间不少于6小时的学生有多少人?21. 如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与DE上的线段AB重合,BE长为0.2米,当踏板连杆绕着点A旋转到AC处时,测得∠CAB=37°,此时点C距离地面的高度CF为0.45米,求AB和AD的长(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)、请补全条形统计图;(2)、求这50名学生每周课外体育活动时间的平均数;(3)、已知该校共有1200名学生,请估计每周课外体育活动时间不少于6小时的学生有多少人?21. 如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与DE上的线段AB重合,BE长为0.2米,当踏板连杆绕着点A旋转到AC处时,测得∠CAB=37°,此时点C距离地面的高度CF为0.45米,求AB和AD的长(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 22. 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
22. 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2). (1)、求m的值和抛物线的解析式;(2)、求不等式x2+bx+c>x+m的解集.(直接写出答案)23. 某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
(1)、求m的值和抛物线的解析式;(2)、求不等式x2+bx+c>x+m的解集.(直接写出答案)23. 某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:销售价格x(元/个)
…
30
40
50
60
…
销售量y(万个)
…
5
4
3
2
…
同时,销售过程中的其他开支(不含进价)总计40万元.
 (1)、以x作为点的横坐标,y作为点的纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察顺次连结各点所得的图形,判断y与x的函数关系,并求出y(万个)与x(元/个)的函数解析式.(2)、求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(3)、该公司要求净得利润不能低于40万元,求出销售价格x(元个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?24. 婆罗摩芨多是公元7世纪古印度伟大的数学家,他在三角形、四边形、零和负数的运算规则,二次方程等方面均有建树,他也研究过对角线互相垂直的圆内接四边形,我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”.
(1)、以x作为点的横坐标,y作为点的纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察顺次连结各点所得的图形,判断y与x的函数关系,并求出y(万个)与x(元/个)的函数解析式.(2)、求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(3)、该公司要求净得利润不能低于40万元,求出销售价格x(元个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?24. 婆罗摩芨多是公元7世纪古印度伟大的数学家,他在三角形、四边形、零和负数的运算规则,二次方程等方面均有建树,他也研究过对角线互相垂直的圆内接四边形,我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”. (1)、若平行四边形ABCD是“婆氏四边形”,则四边形ABCD是.(填序号)
(1)、若平行四边形ABCD是“婆氏四边形”,则四边形ABCD是.(填序号)①矩形;②菱形;③正方形
(2)、如图1,Rt ABC中,∠BAC=90°,以AB为弦的⊙O交AC于D,交BC于E,连接DE、AE、BD,AB=6, ,若四边形ABED是“婆氏四边形”,求DE的长.(3)、如图2,四边形ABCD为⊙O的内接四边形,连接AC,BD,OA,OB,OC,OD,已知∠BOC+∠AOD=180°.①求证:四边形ABCD是“婆氏四边形”;
②当AD+BC=4时,求⊙O半径的最小值.