江苏省徐州市多校2022-2023学年八年级下学期3月月考数学试题
试卷更新日期:2023-04-19 类型:月考试卷
一、单选题
-
1. 下列事件中,是必然事件的是( )A、不共线的三条线段可以组成一个三角形 B、400人中有两个人的生日在同一天 C、早上的太阳从西方升起 D、打开电视机,它正在播放动画片2.
下列四个图形分别是四届国际数学家大会的会标,其中属于中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个3. 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )
A、1个 B、2个 C、3个 D、4个3. 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )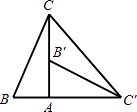 A、45° B、30° C、25° D、15°4. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、矩形的对角线互相垂直 C、一组对边平行的四边形是平行四边形 D、四边相等的四边形是菱形5. 如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )
A、45° B、30° C、25° D、15°4. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、矩形的对角线互相垂直 C、一组对边平行的四边形是平行四边形 D、四边相等的四边形是菱形5. 如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )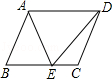 A、20° B、25° C、30° D、35°6. 如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A、20° B、25° C、30° D、35°6. 如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( ) A、点M B、格点N C、格点P D、格点Q7. 如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是( )
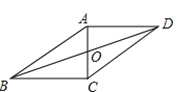
A、点M B、格点N C、格点P D、格点Q7. 如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是( )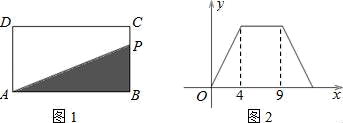 A、10 B、16 C、18 D、208. 如图,菱形中, , , 点、、分别为线段、、上的任意一点,则的最小值为( )
A、10 B、16 C、18 D、208. 如图,菱形中, , , 点、、分别为线段、、上的任意一点,则的最小值为( )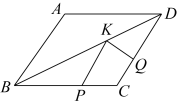 A、4 B、 C、 D、
A、4 B、 C、 D、二、填空题
-
9. 已知:四边形中, , 要使四边形为平行四边形,需添加一个条件是:(只需填一个你认为正确的条件即可).10. 已知菱形中,对角线 , , 面积是.11. 事件A发生的概率为 , 大量重复做这种试验,事件A平均每100次发生的次数是 .
12.如图,为某冷饮店一天售出各种口味雪糕数量的扇形统计图,其中售出红豆口味的雪糕200支,那么售出奶油口味雪糕的数量是 支.
 13.
13.如图,在▱ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= cm.
 14. 如图,在矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=cm.
14. 如图,在矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=cm.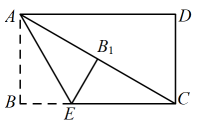 15. 如图,矩形ABCD的面积为5,它的两条对角线交于点O1 , 以AB,AO1为两邻边作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB,AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABCnOn的面积为.
15. 如图,矩形ABCD的面积为5,它的两条对角线交于点O1 , 以AB,AO1为两邻边作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB,AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABCnOn的面积为. 16. 长为1,宽为a的矩形纸片(),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n次操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为
16. 长为1,宽为a的矩形纸片(),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n次操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为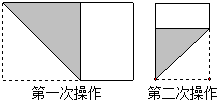
三、解答题
-
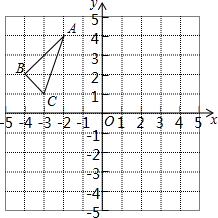
17. 在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
 (1)、按要求作图:
(1)、按要求作图:①画出 关于原点 的中心对称图形 ;
②画出将 绕点 顺时针旋转90°得到 ;
(2)、按照(1)中②作图,回答下列问题: 中顶点 坐标为;若 为 边上一点,则点 对应的点 的坐标为.18. 某市对参加2020年中考的20000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:视力
频数(人)
频率
20
0.1
40
0.2
70
0.35
0.3
10
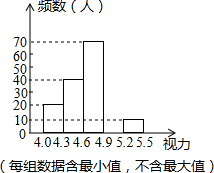 (1)、在频数分布表中, 的值为___, 的值为.(2)、请将频数分布直方图补充完整.(3)、若视力在4.9以上(含4.9)均属正常,根据上述信息估计全市初中毕业生中视力正常的学生有多少人?19. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)、在频数分布表中, 的值为___, 的值为.(2)、请将频数分布直方图补充完整.(3)、若视力在4.9以上(含4.9)均属正常,根据上述信息估计全市初中毕业生中视力正常的学生有多少人?19. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:摸球的次数
100
150
200
500
800
1000
摸到白球的次数
58
96
116
295
484
601
摸到白球的频率
(1)、请估计:当n很大时,摸到白球的频率将会接近;(精确到0.01)(2)、假如你去摸一次,你摸到白球的概率是 , 摸到黑球的概率是;(3)、试估算口袋中黑、白两种颜色的球各有多少只?20. 矩形在平面直角坐标系中的位置如图所示,点B的坐标为 , D是的中点,点E在上,当的周长最小时,求点E的坐标.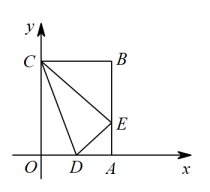 21. 如图,在中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
21. 如图,在中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.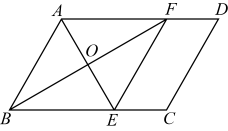 (1)、求证:四边形ABEF是菱形;(2)、若AE=6,BF=8,CE= , 求▱ABCD的面积.22. 如图1,小颖将一组平行的纸条折叠,点 分别落在处,线段与交于点.
(1)、求证:四边形ABEF是菱形;(2)、若AE=6,BF=8,CE= , 求▱ABCD的面积.22. 如图1,小颖将一组平行的纸条折叠,点 分别落在处,线段与交于点.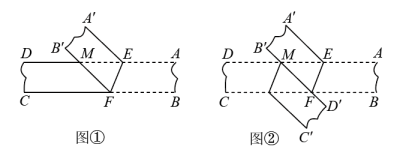 (1)、试判断的形状,并证明你的结论;(2)、如图②,将纸条的另一部分沿折叠,点 , 分别落在 , 处,且使经过点 , 试判断四边形的形状,并证明你的结论;(3)、当度时,四边形是菱形.23. 在矩形中, , E是的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边与、分别相交于点M,N时,观察或测量与的长度,你能得到什么结论?并证明你的结论.
(1)、试判断的形状,并证明你的结论;(2)、如图②,将纸条的另一部分沿折叠,点 , 分别落在 , 处,且使经过点 , 试判断四边形的形状,并证明你的结论;(3)、当度时,四边形是菱形.23. 在矩形中, , E是的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边与、分别相交于点M,N时,观察或测量与的长度,你能得到什么结论?并证明你的结论.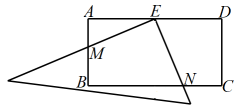 24. 如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
24. 如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.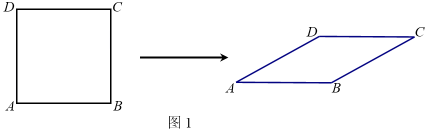 (1)、请补全下表:
(1)、请补全下表:30°
45°
60°
90°
120°
135°
150°
S
1
(2)、填空:由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,;当α=135°时,.由上表可以得到( °);( °),…,由此可以归纳出=S().
(3)、两块相同的等腰直角三角板按如图的方式放置,AD= , ∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).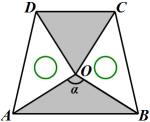 25. 已知,如图,在矩形ABCD中,AB=1,BC=2,点P是直线BC上一个动点,连接AP,作DQ⊥AP于点Q.
25. 已知,如图,在矩形ABCD中,AB=1,BC=2,点P是直线BC上一个动点,连接AP,作DQ⊥AP于点Q.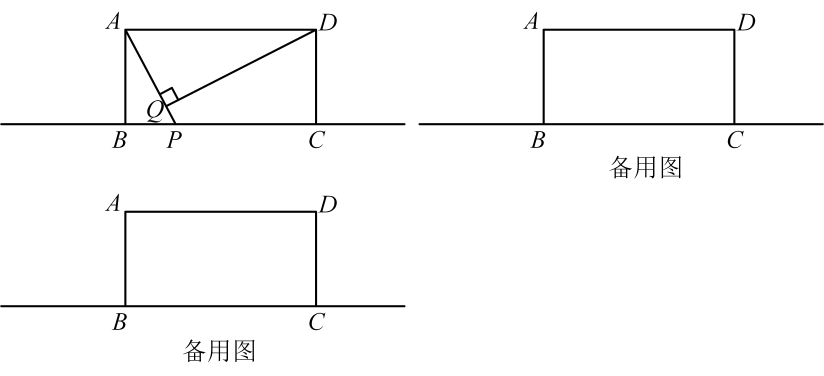 (1)、AP•DQ=;(2)、以AP、AD为邻边作平行四边形APMD,当平行四边形APMD是菱形时,求PQ的长;(3)、连接DP,以AP、DP为邻边作平行四边形APDN,当对角线PN取得最小值时,求DQ的长.
(1)、AP•DQ=;(2)、以AP、AD为邻边作平行四边形APMD,当平行四边形APMD是菱形时,求PQ的长;(3)、连接DP,以AP、DP为邻边作平行四边形APDN,当对角线PN取得最小值时,求DQ的长.