江苏省泰州市兴化市2022-2023学年九年级下学期3月月考数学试题
试卷更新日期:2023-04-19 类型:月考试卷
一、单选题
-
1. 一个不透明的布袋里装有2个白球,3个黄球,它们除颜色外其余都相同,从袋中任意摸出1个球,是黄球的概率为( )A、 B、 C、 D、2. 下列函数中是二次函数的是( )A、 B、 C、 D、3. 如图,在中, , 下列结论中正确的是( )
 A、 B、 C、 D、4. 如图,抛物线y=ax2+bx+c与x轴的一个交点坐标为(﹣2,0),对称轴为直线x=2,其部分图象如图所示,则此抛物线与x轴的另一个交点的坐标为( )
A、 B、 C、 D、4. 如图,抛物线y=ax2+bx+c与x轴的一个交点坐标为(﹣2,0),对称轴为直线x=2,其部分图象如图所示,则此抛物线与x轴的另一个交点的坐标为( )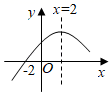 A、(4,0) B、(6,0) C、(8,0) D、(10,0)5. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC的度数是( )
A、(4,0) B、(6,0) C、(8,0) D、(10,0)5. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC的度数是( ) A、35° B、55° C、65° D、70°6. 如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( )
A、35° B、55° C、65° D、70°6. 如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( )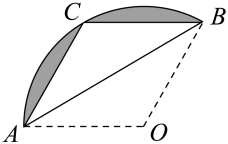 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 已知一组数据2、-2、6、4、-1,这组数据的极差是8. “同时抛掷两枚普通的骰子,向上一面的点数之和为13”是(选填“必然事件”,“不可能事件”,或“随机事件”).9. 已知m是一元二次方程的一个根,则的值是.10. 如图,在 中, ,点 是边 上的一点, 于 ,则边 的长为.
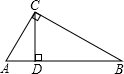 11. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,该圆锥的母线长 ,则扇形的圆心角 度数为.
11. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,该圆锥的母线长 ,则扇形的圆心角 度数为.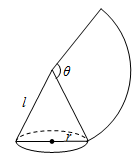 12. 如图,已知在△ABC中,D,E分别是AB,AC上的点, , .若DE=2,则BC的长是.
12. 如图,已知在△ABC中,D,E分别是AB,AC上的点, , .若DE=2,则BC的长是.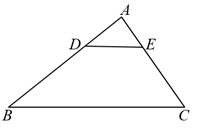 13. 中国古代数学家赵爽用四个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,为直角三角形中的较大锐角,则tan=.
13. 中国古代数学家赵爽用四个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,为直角三角形中的较大锐角,则tan=. 14. 如图,中, , , , 则的内切圆半径为 .
14. 如图,中, , , , 则的内切圆半径为 .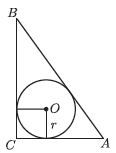 15. 抛物线的顶点D在直线上运动,顶点运动时抛物线也随之运动,抛物线与直线相交于点Q,则点Q纵坐标的最大值为.16. 如图,平面直角坐标系中,点D在直线上,点E为x轴上任意一点,点 , 若为正三角形时,则点D的坐标为.
15. 抛物线的顶点D在直线上运动,顶点运动时抛物线也随之运动,抛物线与直线相交于点Q,则点Q纵坐标的最大值为.16. 如图,平面直角坐标系中,点D在直线上,点E为x轴上任意一点,点 , 若为正三角形时,则点D的坐标为.
三、解答题
-
17.(1)、计算:;(2)、解方程:.18. 某校开展主题为“防疫常识知多少”的调查活动,抽取了部分学生进行调查,调查问卷设置了“A:非常了解”“B:比较了解”“C:基本了解”“D:不太了解”四个等级,要求每个学生填且只能填其中的一个等级,采取随机抽样的方式,并根据调查结果绘制成如图所示不完整的频数分布表和频数直方图,根据以上信息回答下列问题:

等级
频数
频率
A
20
0.4
B
15
b
C
10
0.2
D
a
0.1
(1)、频数分布表中a= ▲ , b= ▲ , 将频数分布直方图补充完整;(2)、若该校有学生1000人,请根据抽样调查结果估算该校“非常了解”和“比较了解”防疫常识的学生共有多少人?(3)、在“非常了解”防疫常识的学生中,某班有3个学生,其中2男1女,计划在这3个学生中随机抽选两个加入防疫志愿者团队,请用列表或画树状图的方法求所选两个学生中有一个女生的概率.19. 我县某校七(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)、甲队成绩的中位数是 , 乙队成绩的众数是;(2)、计算乙队成绩的平均数和方差;(3)、已知甲队成绩的方差是1.4,哪一队的成绩较为整齐?20. 有长为的篱笆,一面利用墙(墙的最大可用长度为),围成中间隔有一道篱笆(平行于)的矩形花圃,设花圃的一边为 , 面积为. (1)、用含有x的代数式表示y;(2)、如果要围成面积为的花圃,的长是多少?21. 如图,已知点 , , 以坐标原点O为位似中心,在第四象限将缩小为原来的三分之一(即新图形与原图形的相似比为).
(1)、用含有x的代数式表示y;(2)、如果要围成面积为的花圃,的长是多少?21. 如图,已知点 , , 以坐标原点O为位似中心,在第四象限将缩小为原来的三分之一(即新图形与原图形的相似比为). (1)、画出缩小后的图形;(2)、写出B点的对应点坐标;(3)、如果内部一点M的坐标为 , 写出点M经位似变换后的对应点坐标.22. 如图,已知矩形中.
(1)、画出缩小后的图形;(2)、写出B点的对应点坐标;(3)、如果内部一点M的坐标为 , 写出点M经位似变换后的对应点坐标.22. 如图,已知矩形中. (1)、请用直尺和圆规在AD上找一点E,使EC平分 , (不写画法,保留画图痕迹);(2)、在(1)的条件下若 , , 求出的值.23. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量 , 两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在 , 两楼之间上方的点处,点距地面的高度为 , 此时观测到楼底部点处的俯角为 , 楼上点处的俯角为 , 沿水平方向由点飞行到达点 , 测得点处俯角为 , 其中点 , , , , , , 均在同一平面内.
(1)、请用直尺和圆规在AD上找一点E,使EC平分 , (不写画法,保留画图痕迹);(2)、在(1)的条件下若 , , 求出的值.23. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量 , 两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在 , 两楼之间上方的点处,点距地面的高度为 , 此时观测到楼底部点处的俯角为 , 楼上点处的俯角为 , 沿水平方向由点飞行到达点 , 测得点处俯角为 , 其中点 , , , , , , 均在同一平面内. (1)、求的长;(2)、求楼与之间的距离的长.(参考数据: , , , ).24. 如图,点是边上的一点,以为直径的交边、于点、.
(1)、求的长;(2)、求楼与之间的距离的长.(参考数据: , , , ).24. 如图,点是边上的一点,以为直径的交边、于点、.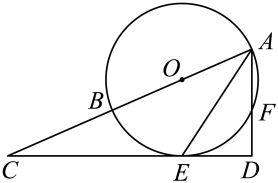
给出下列信息:
①平分;
②;
③直线是的切线.
(1)、请在上述条信息中,选择其中两条作为条件,其余的一条信息作为结论,组成一个真命题.你选择的条件是 ▲ 、 ▲ , 结论是 ▲ (只要填写序号),并说明理由.(2)、在(1)的情况下,若的半径为 , , 求的长.25. 已知抛物线与x轴交于A、B两点(点A在点B的左边),点C是直线上的一个动点. (1)、求该抛物线的对称轴.(2)、若点C是抛物线的顶点,且 , 求a.(3)、已知 , a为大于0的常数,抛物线上有两点M、N,且 , 连接交y轴于点Q,点Q的位置是否发生变化,若不变,请求出Q点坐标;若变化,请说明理由.26. 如图,已知的半径为1,P是平面内一点.(1)、如图①,若 , 过点P作的两条切线、 , 切点分别为E、F,连接.则 , .
(1)、求该抛物线的对称轴.(2)、若点C是抛物线的顶点,且 , 求a.(3)、已知 , a为大于0的常数,抛物线上有两点M、N,且 , 连接交y轴于点Q,点Q的位置是否发生变化,若不变,请求出Q点坐标;若变化,请说明理由.26. 如图,已知的半径为1,P是平面内一点.(1)、如图①,若 , 过点P作的两条切线、 , 切点分别为E、F,连接.则 , . (2)、若点M、N是上两点,且存在 , 则规定点P为的“直角点”.
(2)、若点M、N是上两点,且存在 , 则规定点P为的“直角点”.①如图②,已知平面内有一点D, , 试说明点D是的“直角点”.

②如图③,直线分别与x轴、y轴相交于点A、B,若线段上所有点都是半径为r的圆的“直角点”,求r的最小值与该圆心的坐标.
