浙教版数学八年级下学期常考题微专题训练21三角形的中位线

试卷更新日期：2023-04-18 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，四边形ABCD中，∠B＝90°，AB＝8，BC＝6，点M是对角线AC的中点，点N是AD边的中点，连结BM，MN，若BM＝3MN，则线段CD的长是（）

A、 $\frac{5}{3}$ B、3 C、 $\frac{10}{3}$ D、5

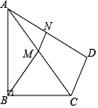查看试题解析
2. 如图所示，点E为平行四边形ABCD对角线AC上的一点，AE＝7，CE＝3，点F在BE的延长线上.且EF＝BE，EF与CD相交于点G，则DF＝（）

A、2 B、3 C、4 D、5

查看试题解析
3. 如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点.若OE=3，则AB的长为（）

A、3 B、6 C、9 D、12

查看试题解析
4. 如图，在四边形ABCD中，点E、F分别为AD、DC的中点，连接EB、BF、EF，△EBF的面积为 $S_{1}$ ．点G为四边形ABCD外一点，连接AG、BG、EG、FG，使得AG＝BC，∠GAB＝∠ABC，△EGF的面积为 $S_{2}$ ，则 $S_{1}$ 与 $S_{2}$ 满足的关系是（）

A、 $S_{1}$ = $S_{2}$ B、2 $S_{1}$ =3 $S_{2}$ C、3 $S_{1}$ =4 $S_{2}$ D、3 $S_{1}$ =2 $S_{2}$

查看试题解析
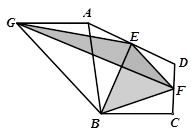5. 如图， ▱ABCD的顶点A，D分别在直角∠MON的两边OM，ON上运动（不与点O重合），▱ABCD的对角线AC，BD相交于点P，连接OP，若OP=5，则▱ABCD的周长最小值是（）

A、20 B、25 C、10 D、15

查看试题解析
6. 如图所示，在△ABC中，D，E分别是边AC，AB的中点，连结BD.若BD平分∠ABC，则下列结论错误的是（）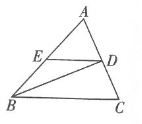

A、BC=2BE B、∠A=∠EDA C、BC=2AD D、BD⊥AC

查看试题解析
7. 如图所示，已知四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从C向D移动而点R不动时，那么下列结论成立的是（）

A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关

查看试题解析
8. 如图，在△ABC中，延长BC至点D，使得CD= $\frac{1}{2}$ BC，过AC的中点E作EF∥CD(点F位于点E右侧)，且EF=2CD，连结DF.若AB=8，则DF的长为（）

A、3 B、4 C、2 $\sqrt{3}$ D、3 $\sqrt{2}$

查看试题解析
9. 如果三角形的两条边分别为4和6，那么连结该三角形三边中点所得的三角形的周长可能是（）

A、6 B、8 C、10 D、12

查看试题解析
10. 在一次活动课中，对如图所示的平行四边形（AD＞AB）进行折叠，第一次沿着AE折叠，点B落在点F处，接着两组同学分别尝试了两种不同的二次折叠，并给出了判断：组1：若沿着CF的中垂线折叠，则点D与点A必重合；组2：若沿着DF折叠，AD与DC所在的直线重合，且点A的对应点仍落在直线AF上，则 $\frac{S_{Δ A B F}}{S ▭_{C F A D}}$ ＝ $\frac{1}{3}$ （）

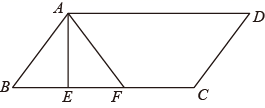A、组1判断正确，组2判断正确 B、组1判断正确，组2判断错误 C、组1判断错误，组2判断正确 D、组1判断错误，组2判断错误

查看试题解析

二、填空题（每题3分，共30分）

11. 如图，在四边形ABCD中，E，F，G，H分别是AB，BD，CD，AC的中点，AD＝4，BC＝5，则四边形EFGH的周长是.

查看试题解析
12. 如图，在▱ $A B C D$ 中， $A C$ 是对角线， $∠ A C D = 90 °$ ，点 $E$ 是 $B C$ 的中点， $A F$ 平分 $∠ B A C$ ， $C F ⊥ A F$ 于点 $F$ ，连接 $E F .$ 已知 $A B = 5$ ， $B C = 13$ ，则 $E F$ 的长为.

查看试题解析
13. 如图，EF是△ABC的中位线，O是EF上一点，且满足OE=2OF.则△ABC的面积与△AOC的面积之比为．

查看试题解析
14. 如图，▱ABCD的顶点C在等边 $△ BEF$ 的边BF上，点E在AB的延长线上，G为DE的中点，连接CG．若AD=5，AB=CF=3，则CG的长为．

查看试题解析
15. 如图，在△ABC中，D，E分别为AB，AC的中点，延长DE到点F，使EF=DE，AB=10，BC=8，则四边形BCFD的周长为.

查看试题解析
16. 如图，在平行四边形ABCD中，E是CD的中点，F是AE的中点，CF交BE于点G ，若BE＝8，则GE＝．

查看试题解析

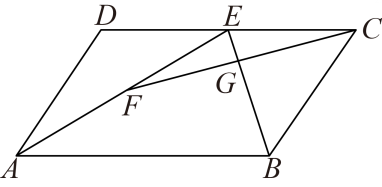
三、解答题（共7题，共66分）

17. 已知：如图，在△ABC中，CF平分∠ACB， $C A = C D$ ， $A E = E B$ .求证： $E F = \frac{1}{2} B D$ .

查看试题解析
18. 在Rt△ABC中，∠BAC＝90°，E、F分别是BC、AC的中点，延长BA到点D，使AB＝2AD，连接DE、DF、AE、EF，AF与DE交于点O.

(1)、试说明AF与DE互相平分；

(2)、若AB＝8，BC＝12，求DE的长.

查看试题解析
19. 如图，在△ABC中，AB＝13，AC＝23，点D在AC上，若BD＝CD＝10，AE平分∠BAC ．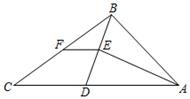

(1)、求AE的长；

(2)、若F是BC中点，求线段EF的长．

查看试题解析
20. 如图，点D、E、F分别是△ABC的边AB、BC、AC的中点，延长DE至点G，使得DE=EG，连接AE，FG.

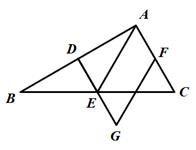(1)、求证：四边形AEGF是平行四边形．

(2)、若∠BAC＝90°，AD＝AC＝ $3$ ，求FG的长．

查看试题解析
21. 如图，在▱ $A B C D$ 中，点 $G$ ， $H$ 分别是 $A B$ ， $C D$ 的中点，点 $E$ ， $F$ 在对角线 $A C$ 上，且 $A E = C F$ .

(1)、求证：四边形 $E G F H$ 是平行四边形；

(2)、连接 $B D$ 交 $A C$ 于点 $O$ ，若 $B D = 10$ ， $A E + C F = E F$ ，求 $E G$ 的长.

查看试题解析
22. 如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使 $B F = B E$ ，连接EC并延长，使 $C G = C E$ ，连接FG，H为FG的中点，连接DH

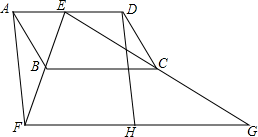(1)、求证：四边形AFHD为平行四边形；

(2)、若 $C B = C E$ ， $∠ E B C = 75 °$ ， $∠ D C E = 10 °$ ，求 $∠ D A B$ 的度数.

查看试题解析
23. 【发现与证明】
如图，在四边形ABCD中，E、F、G、H是各边中点，对角线AC、BD相交于点O，I、J是AC、BD的中点，连接EF、EH、HG、GF、EI、GI、EJ、FJ、IJ、GJ、IH.
结论1：四边形EFGH是平行四边形；
结论2：四边形EJGI是平行四边形；
结论3： $S_{四边形 E F G H} = \frac{1}{2} S_{四边形 A B C D}$ ；
……

(1)、请选择其中一个结论，加以证明（只需证明一个结论）.

(2)、【探究与应用】（★温馨提示：以下问题可以直接使用上述结论）
①如图1，在四边形ABCD中，F、H分别为边AB，DC的中点，连结HF.已知 $A D = 6$ ， $B C = 4$ ，线段HF的取值范围是 ▲ .
②如图2，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，连接EG，FH交于点O， $E G = 8$ cm， $F H = 6$ cm， $∠ E O F = 60 °$ ，求 $S_{四边形 A B C D}$ .

查看试题解析