苏科版常考题微专练：整式的混合运算（七年级第二学期数学复习）

试卷更新日期：2023-04-18 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共16分）

1. 若 $a^{2} - 2 a - 1 = 0$ ，那么代数式 $(a + 2) (a - 2) - 2 a$ 的值为（）

A、 $- 1$ B、 $- 3$ C、1 D、3

查看试题解析
2. 一个长方体的长、宽、高分别为 $2 x$ 、 $2 x - 1$ 、 $x^{2}$ ，它的体积等于（）

A、 $4 x^{4} - 4 x^{2}$ B、 $4 x^{4} - 2 x^{3}$ C、 $4 x^{3} - 2 x^{2}$ D、 $4 x^{4}$

查看试题解析
3. 若 $M = (x - 2) (x - 5)$ ， $N = (x - 3) (x - 4)$ ，则 $M$ 与 $N$ 的大小关系为（）

A、 $M > N$ B、 $M = N$ C、 $M < N$ D、由 $x$ 的取值而定

查看试题解析
4. 如图，两个正方形边长分别为a、b，如果a+b=ab=6，则阴影部分的面积为（）

A、6 B、9 C、12 D、18

查看试题解析
5. 现有一张边长为 $a$ 的大正方形卡片和三张边长为 $b$ 的小正方形卡片 $(\frac{1}{2} a < b < a)$ 如图 $1$ ，取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图 $2$ ，再重新用三张小正方形卡片放入“大正方形卡片”内拼成的图案如图 $3$ ，已知图 $3$ 中的阴影部分的面积比图 $2$ 中的阴影部分的面积大 $2 a b - 15$ ，则小正方形卡片的面积是（）

A、 $10$ B、 $8$ C、 $2$ D、 $5$

查看试题解析
6. 下列计算：① $x (2 x^{2} - x + 1) = 2 x^{3} - x^{2} + 1$ ；② ${(a - b)}^{2} = a^{2} - b^{2}$ ；③ ${(x - 4)}^{2} = x^{2} - 4 x + 16$ ；④ $(5 a - 1) (- 5 a - 1) = 25 a^{2} - 1$ ；⑤ ${(- a - b)}^{2} = a^{2} + 2 a b + b^{2}$ .其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知 $a_{1}$ ， $a_{2}$ ，…， $a_{2020}$ 都是正数，如果 M＝（ $a_{1}$ + $a_{2}$ +…+ $a_{2019}$ ）（ $a_{2}$ + $a_{3}$ +…+ $a_{2020}$ ），N＝（ $a_{1}$ + $a_{2}$ +…+ $a_{2020}$ ）（ $a_{2}$ + $a_{3}$ +…+ $a_{2019}$ ），那么 M，N 的大小关系是（）

A、M＞N B、M＝N C、M＜N D、不确定

查看试题解析
8. 为了书写简便，数学家欧拉引进了求和符号“ $\sum$ ”．如记 $\sum_{k = 1}^{n} k = 1 + 2 + 3 + ... + (n - 1) + n MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaaqahabaGaam4Aaiab
g2da9iaaigdacqGHRaWkcaaIYaGaey4kaSIaaG4maiabgUcaRiaac6
cacaGGUaGaaiOlaiabgUcaRmaabmaapaqaa8qacaWGUbGaeyOeI0Ia
aGymaaGaayjkaiaawMcaaiabgUcaRiaad6gaaSqaaiaadUgacqGH9a
qpcaaIXaaabaGaaeOBaaqdcqGHris5aaaa@5506@$ ， $\sum_{k = 3}^{n} (x + k) = (x + 3) + (x + 4) + ... + (x + n) MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaaqahabaWaaeWaa8aa
baWdbiaadIhacqGHRaWkcaWGRbaacaGLOaGaayzkaaGaeyypa0Zaae
Waa8aabaWdbiaadIhacqGHRaWkcaaIZaaacaGLOaGaayzkaaGaey4k
aSYaaeWaa8aabaWdbiaadIhacqGHRaWkcaaI0aaacaGLOaGaayzkaa
Gaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSYaaeWaa8aabaWdbiaa
dIhacqGHRaWkcaWGUbaacaGLOaGaayzkaaaaleaacaWGRbGaeyypa0
JaaG4maaqaaiaad6gaa0GaeyyeIuoaaaa@5C66@$ ，已知 $\sum_{k = 2}^{n} [(x + k) (x - k + 1)] = 4 x^{2} + 4 x + m MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaawahabeWcpaqaa8qa
caWGRbGaeyypa0JaaGOmaaWdaeaapeGaamOBaaqdpaqaa8qacqGHri
s5aaGcdaWadaWdaeaapeWaaeWaa8aabaWdbiaadIhacqGHRaWkcaWG
RbaacaGLOaGaayzkaaWaaeWaa8aabaWdbiaadIhacqGHsislcaWGRb
Gaey4kaSIaaGymaaGaayjkaiaawMcaaaGaay5waiaaw2faaiabg2da
9iaaisdacaWG4bWdamaaCaaaleqabaWdbiaaikdaaaGccqGHRaWkca
aI0aGaamiEaiabgUcaRiaad2gaaaa@5A83@$ ，则m的值是（）

A、-50 B、-70 C、-40 D、-20

查看试题解析

二、填空题（每题2分，共16分）

9. ﹣y³•y⁵÷（﹣y）⁴＝.

查看试题解析
10. $9 m^{2} - 5 m + 1 +$ = ${(3 m - 1)}^{2}$ .

查看试题解析
11. 已知 $x^{2} + x - 1 = 0$ ，则代数式 $x (x + 3) + (x + 2) (x - 3)$ 的值为.

查看试题解析
12. 若 $(1 + m) (2 + m) = 3$ ，则 $(1 + m)^{2} + (2 + m)^{2} =$ .

查看试题解析
13. 若m²=n+2022，n²=m+2022（m≠n），那么代数式m³-2mn+n³的值．

查看试题解析
14. 用如图所示的正方形和长方形卡片若干张，拼成一个边长为a＋3b的正方形，需要B类卡片张.

查看试题解析
15. 小亮用边长为a的正方形纸片，边长为b的正方形纸片，及边长分别为a和b的长方形纸片，各若干张，拼出了邻边长分别为3a+b和4a+3b的大长方形，那么小亮用了三种纸片一共张.

查看试题解析
16. 在计算 $(x + y) (x - 3 y) - m y (n x - y)$ （m、n均为常数）的值，在把x、y的值代入计算时，粗心的小明把y的值看错了，其结果等于9，细心的小红把正确的x、y的值代入计算，结果恰好也是9，为了探个究竟，小红又把y的值随机地换成了2018，结果竟然还是9，根据以上情况，探究其中的奥妙，计算mn=.

查看试题解析

三、计算题（共5题，共34分）

17. 计算：

(1)、 $3^{0} - 2^{- 3} + {(- 3)}^{2} - {(\frac{1}{4})}^{- 1}$ ；

(2)、 ${(- a^{2})}^{3} - 6 a^{2} \cdot a^{4}$ .

查看试题解析
18. 计算：

(1)、 ${(- 2022)}^{0} - {(\frac{1}{2})}^{- 2} + {(- 2)}^{3}$ ；

(2)、 ${(3 a - b)}^{2} - (a - 3 b) (a + 3 b)$ ．

查看试题解析
19. 先化简，再求值： $(3 a + 1) (3 a - 1) - 9 a (a - 1)$ ，其中 $a = 2$ ．

查看试题解析
20. 先化简，再求值： $a (4 b - 5 a) + (2 a + b) (b - 2 a) + {(3 a - b)}^{2}$ ，其中 $a = 2 ， b = - 3$ ．

查看试题解析
21. 先化简，再求值： $(x + 3) (x - 1) + (x - 2) (x + 2) - 2 {(x - 1)}^{2}$ ，其中 $x = \frac{1}{3}$ ．

查看试题解析

四、解答题（共6题，共54分）

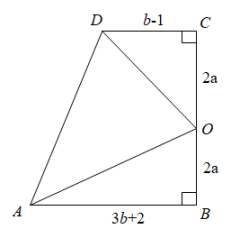
22. 有这样一道题：计算（2x﹣3）（3x+1）﹣6x（x+3）+25x+15的值，其中x=2018．小刚把x=2018错抄成x=2081，但他的计算结果也是正确的，请通过计算说明原因．

查看试题解析
23. 有些同学会想当然地认为 $(x - y)^{3} = x^{3} - y^{3}$ ．

(1)、举出反例说明该式不一定成立；

(2)、计算 $(x - y)^{3}$ ；

(3)、直接写出当 $x$ 、 $y$ 满足什么条件，该式成立．

查看试题解析
24. 解决下列问题：

(1)、若4a-3b+7=0，求3²×9^2a+1÷27^b的值；

(2)、已知x满足2^2x+4-2^2x+2=96，求x的值.

(3)、对于任意有理数A，B，C，D，我们规定符号（a，b）⋇（c，d）=ad-bc+2，例如：（1，3）⋇（2，4）=1×4-2×3+2=0.当a²+a+5=0时，求（2a+1，a-2）⋇（3a+2，a-3）的值.

查看试题解析
25. 如图所示，直角梯形ABCD中，O是BC的中点，求 $△ A D O$ 的面积（用含a，b的式子表示）．

查看试题解析
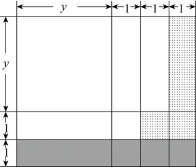
26. 提出问题：怎么运用矩形面积表示（y+2）（y+3）与2y+5的大小关系（其中y>0）？
几何建模：
（1）画长y+3，宽y+2的矩形，按图方式分割
（2）变形：2y+5=（y+2）+（y+3）
（3）分析：图中大矩形的面积可以表示为（y+2）（y+3）；阴影部分面积可以表示为（y+3）×1，画点部分的面积可表示为y+2，由图形的部分与整体的关系可知：

（y+2）（y+3）＞（y+2）+（y+3），即（y+2）（y+3）＞2y+5

归纳提炼：

当a>2，b>2时，表示ab与a+b的大小关系．根据题意，设a=2+m，b=2+n（m>0，n>0），要求参照上述研究方法，画出示意图，并写出几何建模步骤（用铅笔画图，并标注相关线段的长）

查看试题解析
27. 【知识回顾】
七年级学习代数式求值时，遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式＝（a+3）x﹣6y+5，所以a+3＝0，则a＝﹣3．
【理解应用】

(1)、若关于x的多项式（2x﹣3）m+2m²﹣3x的值与x的取值无关，求m值；

(2)、已知A＝（2x+1）（x﹣1）﹣x（1﹣3y），B＝﹣x²+xy﹣1，且3A+6B的值与x无关，求y的值；

(3)、【能力提升】
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为S₁ ，左下角的面积为S₂ ，当AB的长变化时，S₁﹣S₂的值始终保持不变，求a与b的等量关系．

查看试题解析