苏科版常考题微专练:平方差公式(七年级第二学期数学复习)
试卷更新日期:2023-04-18 类型:复习试卷
一、单选题(每题2分个,共16分)
-
1. 下列各式不能运用平方差公式计算的是( )A、 B、 C、 D、2. 下列各式能用平方差公式计算的是( )A、(-2x+y)(-2x-y) B、(2x+y)(x-2y) C、(x-2y)(-x+2y) D、(-2x+y)(-x+2y)3. 下列各式能用平方差公式计算的是( )A、(﹣a+1)(﹣a﹣1) B、(2x+y)(2y﹣x) C、(a+b)(a﹣2b) D、(2x﹣1)(﹣2x+1)4. 的计算结果是( )A、 B、 C、 D、5. 已知a+b=﹣3,a﹣b=1,则a2﹣b2的值是( )A、1 B、-2 C、﹣3 D、106. 已知a﹣b=2,则a2﹣b2﹣4b的值为( )A、5 B、4 C、2 D、17. 我们知道,借助图形可以验证公式.下列图形可以用来验证平方差公式a2−b2=(a+b)(a−b)的是( )A、
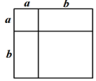 B、
B、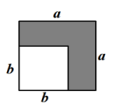 C、
C、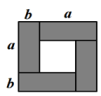 D、
D、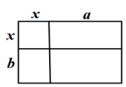 8. 算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是( )A、4 B、2 C、8 D、6
8. 算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是( )A、4 B、2 C、8 D、6二、填空题(每题2分,共16分)
-
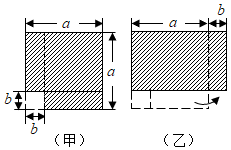
9. 若 , , 则 .10. 若 , 则的值是11. 若 , 则代数式的值等于 .12. 计算: .13. 将图(甲)中阴影部分的小长方形变换到图(乙)位置,根据两个图形的面积关系得到的恒等式是:.
 14. 计算 的结果为.15. 已知两个正方形的边长的和为20cm,它们的面积的差为40cm2 , 则这两个正方形的边长分别是 cm.
14. 计算 的结果为.15. 已知两个正方形的边长的和为20cm,它们的面积的差为40cm2 , 则这两个正方形的边长分别是 cm.三、计算题
-
16. 计算:(1)、2a(a-2a2)(2)、(x-2y-1)(x+2y-1)17. 计算:(1)、;(2)、;(3)、.18. 计算(1)、6x3-x(x2+1)(2)、a3·a4·a+(a2)4+(-2a4)2(3)、99x101(4)、(a-b)2 -(a+b)(a-b)19. 计算:(1)、(2)、(x-y+3)(x+y-3)(3)、(4)、
四、解答题(共3题,共36分)
-
20. 从边长为 a 的正方形剪掉一个边长为 b 的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).
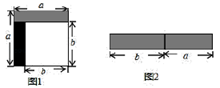 (1)、上述操作能验证的等式是 (请选择正确的一个)A、a ﹣2ab+b =(a﹣b) B、a ﹣b =(a+b)(a﹣b) C、a +ab=a(a+b)(2)、若 x ﹣9y =12,x+3y=4,求 x﹣3y 的值;(3)、计算: .21. 将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形,1号正方形的边长为x,2号正方形的边长为y.
(1)、上述操作能验证的等式是 (请选择正确的一个)A、a ﹣2ab+b =(a﹣b) B、a ﹣b =(a+b)(a﹣b) C、a +ab=a(a+b)(2)、若 x ﹣9y =12,x+3y=4,求 x﹣3y 的值;(3)、计算: .21. 将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形,1号正方形的边长为x,2号正方形的边长为y.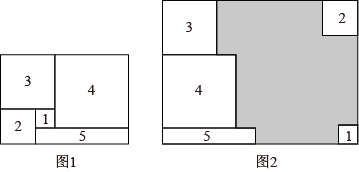 (1)、求5号长方形的面积(用含x,y的代数式表示);(2)、若图1中长方形的周长为24.
(1)、求5号长方形的面积(用含x,y的代数式表示);(2)、若图1中长方形的周长为24.①若2号正方形与1号正方形的面积差为3,求5号长方形的面积;
②将图1中的1号、2号、3号、4号四个正方形和5号长方形按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为 ▲ .
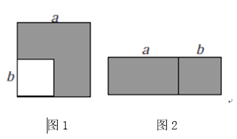
22.(1)、【知识情境】通常情况下,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
如图1,在边长为a的正方形中挖掉一个边长为b的小正方形 (a>b) .把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是;
 (2)、【拓展探究】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.
(2)、【拓展探究】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.如图3是边长为 的正方体,被如图所示的分割线分成8块.
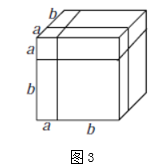
用不同的方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式可以为:
;
(3)、已知 , ,利用上面的恒等式求 的值.