黑龙江省哈尔滨市南岗区2022-2023学年九年级下学期中考模拟练习卷(三)数学(五四制)学科试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 实数2,0,﹣2, 中,为负数的是( )A、2 B、0 C、﹣2 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
4. 四个相同的小正方形组成的立体图形如图所示,它的主视图为( )
斐波那契螺旋线
4. 四个相同的小正方形组成的立体图形如图所示,它的主视图为( )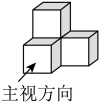 A、
A、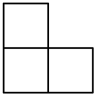 B、
B、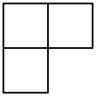 C、
C、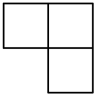 D、
D、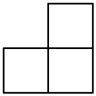 5. 如图, 是 的切线,点A为切点, 交 于点B , ,点C在 上, .则 等于( )
5. 如图, 是 的切线,点A为切点, 交 于点B , ,点C在 上, .则 等于( )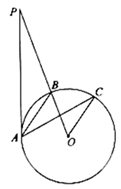 A、20° B、25° C、30° D、50°6. 分式方程 的解为( )A、 B、 C、 D、7. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )
A、20° B、25° C、30° D、50°6. 分式方程 的解为( )A、 B、 C、 D、7. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )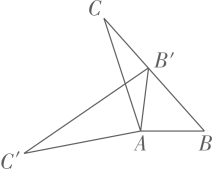 A、 B、 C、 D、8. 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )A、 B、 C、 D、9. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( )
A、 B、 C、 D、8. 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )A、 B、 C、 D、9. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( ) A、 B、 C、 D、10. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
A、 B、 C、 D、10. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )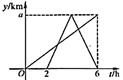 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
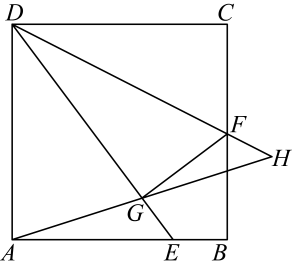
11. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1 700 000年误差不超过1秒.数据1 700 000用科学记数法表示 .12. 若代数式 在实数范围内有意义,则x的取值范围是 .13. 已知点(2,-2)在反比例函数的图象上,则k的值为 .14. 计算: .15. 分解因式: =.16. 抛物线 的顶点坐标为 .17. 不等式组的解集是 .18. 若一个扇形的圆心角为 ,面积为 ,则这个扇形的弧长为 (结果保留 )19. 在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为度.20. 如图,E是正方形边上一点,连接平分交于点F.过F作 , 垂足为G,连接并延长交延长线于点H,若 , 则 .
三、解答题
-
21. 先化简,再求代数式的值,其中22. 如图,在小正方形边长均为1的方格纸中有线段AB,点A、B均在小正方形的顶点上.
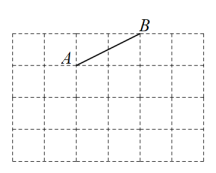 (1)、以AB为一边画Rt△ABC(点C在小正方形的顶点上),使△ABC的周长为+5;(2)、在(1)的条件下,以AB为一边作△ABD,(点D在小正方形的顶点上),使 , 且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.23. 某小区开展以“我最喜爱的电商平台”为主题的调查活动,围绕“在淘宝、唯品会、JD京东,易购、天猫共五个平台中,你最喜爱在哪一电商平台购物?(每户家庭必选且只选一类)”的问题,在小区范围内随机抽取部分家庭进行问卷调查,将调查结果整理后绘制成如图1、图2所示的不完整的统计图.请你根据图中提供的信息回答下列问题:
(1)、以AB为一边画Rt△ABC(点C在小正方形的顶点上),使△ABC的周长为+5;(2)、在(1)的条件下,以AB为一边作△ABD,(点D在小正方形的顶点上),使 , 且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.23. 某小区开展以“我最喜爱的电商平台”为主题的调查活动,围绕“在淘宝、唯品会、JD京东,易购、天猫共五个平台中,你最喜爱在哪一电商平台购物?(每户家庭必选且只选一类)”的问题,在小区范围内随机抽取部分家庭进行问卷调查,将调查结果整理后绘制成如图1、图2所示的不完整的统计图.请你根据图中提供的信息回答下列问题: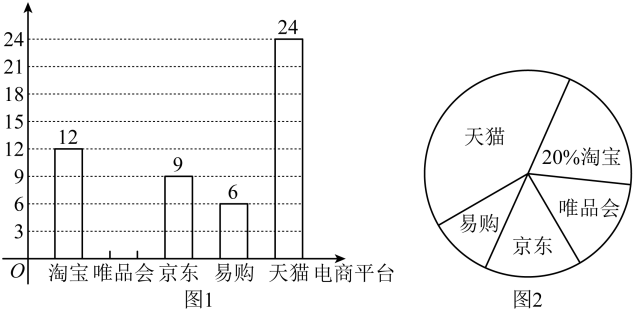 (1)、本次调查共抽取了多少户家庭?(2)、求在本次调查的家庭中,最喜爱在唯品会购物的家庭数量,并补全条形统计图;(3)、若小区有户家庭,请你估计该小区最喜欢在京东购物的家庭有多少户?24. 如图1,平行四边形中,点E、点F分别是上的点,连接 , .
(1)、本次调查共抽取了多少户家庭?(2)、求在本次调查的家庭中,最喜爱在唯品会购物的家庭数量,并补全条形统计图;(3)、若小区有户家庭,请你估计该小区最喜欢在京东购物的家庭有多少户?24. 如图1,平行四边形中,点E、点F分别是上的点,连接 , .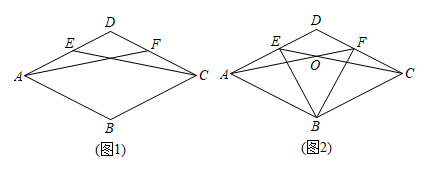 (1)、求证:四边形是菱形.(2)、如图2,当点E是AD中点时,与交于点O,连接 , 请直接写出图2中四个三角形,使写出的每个三角形的面积等于面积3倍.25. 今年6月以来,我国多地遭遇强降雨,引发洪涝灾害,人民的生活受到了极大的影响,“一方有难,八方支援”,某市筹集了大量的生活物资,用A,B两种型号的货车,分两批运往受灾严重的地区,具体运算情况如下:
(1)、求证:四边形是菱形.(2)、如图2,当点E是AD中点时,与交于点O,连接 , 请直接写出图2中四个三角形,使写出的每个三角形的面积等于面积3倍.25. 今年6月以来,我国多地遭遇强降雨,引发洪涝灾害,人民的生活受到了极大的影响,“一方有难,八方支援”,某市筹集了大量的生活物资,用A,B两种型号的货车,分两批运往受灾严重的地区,具体运算情况如下:第一批
第二批
A型货车的辆数(单位:辆)
1
2
B型货车的辆数(单位:辆)
3
5
累计运送货物的吨数(单位:吨)
28
50
备注:第一批、第二批每辆货车均满载
(1)、求A,B两种型号货车每辆满载分别能运多少吨生活物资;(2)、该市后续又筹集了62.4吨生活物资,现已联系了3辆A型号货车,试问至少还需联系多少辆B型号货车才能一次性将这批生活物资运往目的地.26. 已知和分别切于点B和C,D是上一点,连接 .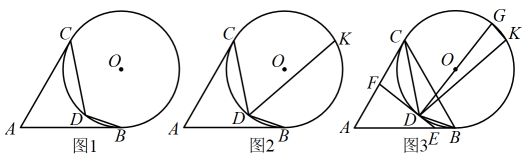 (1)、如图1,求证:;(2)、如图2,作的平分线交于点K,当时,求证:;(3)、如图3,在(2)的条件下,过D的切线分别交于点E,F,作直径 , 连接 , 当F是的中点时, , 求线段的长.27. 如图,在平面直角坐标系中,点О为坐标原点,抛物线与x轴交于A,B两点,与y轴交于点C, .
(1)、如图1,求证:;(2)、如图2,作的平分线交于点K,当时,求证:;(3)、如图3,在(2)的条件下,过D的切线分别交于点E,F,作直径 , 连接 , 当F是的中点时, , 求线段的长.27. 如图,在平面直角坐标系中,点О为坐标原点,抛物线与x轴交于A,B两点,与y轴交于点C, .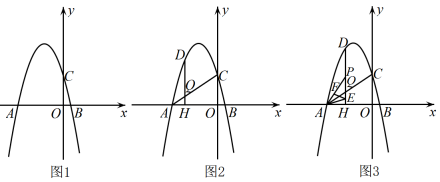 (1)、求抛物线的解析式;(2)、点D为第二象限抛物线上一点,过点D作轴,垂足为H,连接交于点Q,设点D的横坐标为t,线段的长为d,求d与t的函数关系式;(3)、在(2)的条件下,点Р在上, , 连接PA,点E,F分别在 , 上,连接 , , , , 求点Р的坐标.
(1)、求抛物线的解析式;(2)、点D为第二象限抛物线上一点,过点D作轴,垂足为H,连接交于点Q,设点D的横坐标为t,线段的长为d,求d与t的函数关系式;(3)、在(2)的条件下,点Р在上, , 连接PA,点E,F分别在 , 上,连接 , , , , 求点Р的坐标.